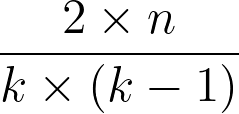Projeto 1 de Teoria e Aplicação de Grafos, disciplina ofertada na Universidade de Brasília (UnB) no semestre 2021.1.
O objetivo principal é aplicar o algoritmo de Bron-Kerbosh para encontrar os cliques maximais de um grafo não-direcionado. O algoritmo é utilizado na forma sem pivotamento e com pivotamento. O programa também mostra o coeficiente médio de aglomeração do grafo dado.
O programa lê um arquivo .mtx, em que cada linha representa uma aresta entre dois vértices enumerados. Para o programa, é usado o arquivo soc-dolphins.mtx, montado a partir do artigo “David Lusseau et al., The bottelenose dolphin community of Doubful Sound features a large proportion of long-lasting associations, Journal of Behavioral Ecology and Sociobiology 54:4, 396--405 (2003).” e disponibilizado pelo professor da disciplina, Díbio Leandro Borges.
Esse arquivo mapeia as relações estabelecidas entre 62 golfinhos em um grafo não direcionado.
O algoritmo foi implementado utilizando um grafo representado por listas de adjacências. Como esse algoritmo geralmente é descrito em termos de conjuntos, as listas foram substituídas por sets em Python, permitindo fazer a tradução do pseudo código para código de uma forma direta.
O pseudo código que serviu de base para a implementação do algoritmo de Bron-Kerbosh pode ser encontrado no OpenGenus IQ e podendo ser visto na abaixo:
BronKerbosch1(R, P, X):
se P e X estão ambos vazios:
retorna R como clique maximal
para cada vértice v em P:
BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}
Na primeira iteração, portanto, temos os conjuntos R e X vazios, com P sendo a lista de todos os nós do grafo.
Para o algoritmo com pivotamento, foi utilizado pseudo código descrito em Brito e Santos (2011). O método de pivotamento escolhido foi o de grau máximo. Assim, cada iteração do algoritmo sem pivotamento agora recebe não passa para um vértice qualquer em P, e sim um pivô - no caso, o vértice de maior grau em P.
O pseudo código utilizado pode ser visto abaixo:
BronKerbosch2(R, P, X):
se P e X estão ambos vazios:
retorna R como clique maximal
para o pivô v em P, o vértice de maior grau:
BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}
O coeficiente médio de aglomeração de um grafo é a média de todos os coeficientes locais de aglomeração. Este, por sua vez, descreve a relação entre a quantidade de vizinhos de um vértice que são vizinhos entre si e o grau desse mesmo vértice. O cálculo do coeficiente local pode ser visto abaixo:
Em que k é o grau do vértice v e n é o número de vizinhos de v que são vizinhos entre si.
Para utilizar o projeto desenvolvido, é necessário que o arquivo soc.dolphins.mtx esteja na mesma pasta do código .py. Caso queira utilizar-se um outro arquivo .mtx, é necessário alterar no código fonte.
Com isso, basta compilar o arquivo .py no terminal.
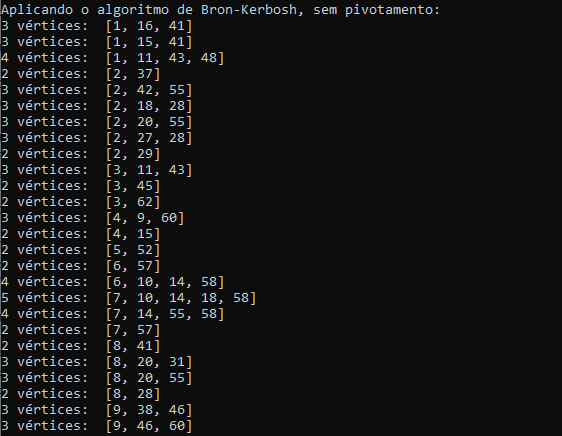
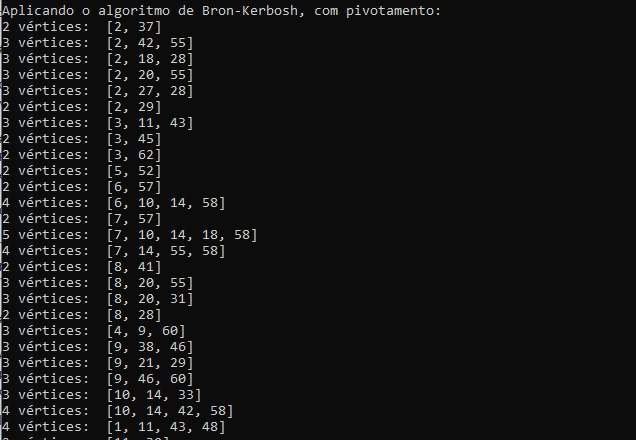
python tag_p1_202033202.pyA interface com o usuário é exibida através do terminal. Nele, quando o código é compilado, são exibidas três seções: cada clique máximo obtido pelo algoritmo sem pivotamento, com o total na linha final; cada clique máximo obtido pelo algoritmo com pivotamento, com o total na linha final; e o coeficiente máximo de aglomeração do grafo.
Nas figuras abaixos é possível ver capturas de tela de trechos cada uma dessas seções.