cs-maps-tree-map-lab

Learning goals

Implement the Map interface using a binary search tree.
Analyze the performance of a tree-backed map.

Overview

At this point you should be familiar with the Map interface and the HashMap implementation provided by Java. And by making your own Map using a hash table, you should understand how HashMap works and why we expect its core methods to be constant time.

Because of this performance, HashMap is widely used, but it is not the only implementation of Map. There are two reasons you might want another implementation:

Hashing can be slow, so even though HashMap operations are constant time, the "constant" might be big.
The keys in a hash table are not stored in any particular order; in fact, the order might change when the table grows and the keys are rehashed. For some applications, it is necessary, or at least useful, to keep the keys in order.

It turns out to be hard to solve both of these problems at the same time, but Java provides an implementation called TreeMap that comes close:

The order of growth is not quite as good. Instead of constant time, a TreeMap takes time proportional to log n.
Inside the TreeMap, the keys are not stored in order; they are stored in a binary search tree, which makes it possible to traverse the keys, in order, in linear time.

In this lab, we'll explain how binary search trees work and then you will use one to implement a Map. Along the way, we'll analyze the performance of the core map methods when imlemented using a tree.

Binary search tree

A binary search tree (BST) is a tree where each node contains a key, and every node has the "BST property":

If node has a left child, all keys in the left subtree must be less than the key in node.
If node has a right child, all keys in the right subtree must be greater than the key in node.

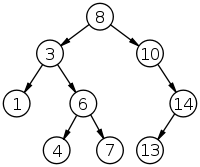
The following diagram shows a tree of integers that has this property.

This figure is from the Wikipedia page on binary search trees, which you might find useful while you work on this lab.

The key in the root is 8, and you can confirm that all keys to the left of the root are less than 8, and all keys to the right are greater. You can also check that the other nodes have this property.

Looking up a key in a binary search tree is fast because we don't have to search the entire tree. Starting at the root, we can use the following algorithm:

Compare the key you are looking for, target, to the key in the current node. If they are equal, you are done.
If target is less than the current key, search the left tree. If there isn't one, target is not in the tree.
If target is greater than the current key, search the right tree. If there isn't one, target is not in the tree.

At each level of the tree, you only have to search one child. For example, if you look for target = 4 in the previous diagram, you start at the root, which contains the key 8. Because target is less than 8, you go left. Because target is greater than 3 you go right. Because target is less than 6, you go left. And then you find the key you are looking for.

In this example, it takes 4 comparisons to find the target, even though the tree contains 9 keys. In general, the number of comparisons is proportional to the height of the tree, not the number of keys in the tree.

So what can we say about the relationship between the height of the tree, h, and the number of nodes, n? Starting small and working up:

If h=1, the tree only contains one node, so n=1.
If h=2, we can add two more nodes, for a total of n=3.
If h=3, we can add up to 4 more nodes, for a total of n=7.
If h=4, we can add up to 8 more nodes, for a total of n=15.

By now you might see the pattern. If we number the levels tree from 1 to h, the level with index i can have up to 2^i-1 nodes. And the total number of nodes in h levels is 2^h-1. If we have

n = 2^h - 1

We can take the log base 2 of both sides:

log₂ ≈ h

Which means that the height of the tree is proportional to log n, if the tree is full; that is, if each level contains the maximum number of nodes.

So we expect that we can look up a key in a binary search tree in time proportional to log n. This is true if the tree is full, and even if the tree is only partially full. But it is not always true, as we will see.

An algorithm that takes time proportional to log n is called "logarithmic" or "log time", and it belongs to the order of growth O(log n).

Implementing a tree-backed `Map`

In this section we'll describe the starter code for this lab; in the next section we'll give you instructions for filling in the missing methods.

Here's the beginning of our implementation, called MyTreeMap:

public class MyTreeMap<K, V> implements Map<K, V> {

	private int size = 0;
	private Node root = null;

The instance variables are size, which keeps track of the number of keys, and root, which is a reference to the root node in the tree. When the tree is empty, root is null and size is 0.

Here's the definition of Node, which is defined inside MyTreeMap:

	protected class Node {
		public K key;
		public V value;
		public Node left = null;
		public Node right = null;

		public Node(K key, V value) {
			this.key = key;
			this.value = value;
		}
	}

Each node contains a key-value pair and references to two child nodes, left and right. Either or both of the child nodes can be null.

Some of the Map methods are easy to implement, like size and clear:

	public int size() {
		return size;
	}

	public void clear() {
		size = 0;
		root = null;
	}

size is clearly constant time.

clear appears to be constant time, but consider this: when root is set to null, the garbage collector reclaims the nodes in the tree, which takes linear time. Should work done by the garbage collector count? We think so.

In the next section, you'll fill in some of the other methods, including the most important ones, get and put.

Instructions

When you check out the repository for this lab, you should find a file structure similar to what you saw in previous labs. The top level directory contains CONTRIBUTING.md, LICENSE.md, README.md, and the directory with the code for this lab, javacs-lab09.

In the subdirectory javacs-lab09/src/com/flatironschool/javacs you'll find these source files:

MyTreeMap.java contains the code from the previous section with outlines for the missing methods.
MyTreeMapTest.java contains the unit tests for MyTreeMap.

Also, in javacs-lab09, you'll find the Ant build file build.xml.

In javacs-lab09, run ant build to compile the source files. Then run ant test, which runs MyTreeMapTest. Several tests should fail, because you have some work to do!
We've provided outlines for get and containsKey. Both of them use findNode, which is a private method we defined; it is not part of the Map interface. Here's how it starts:

	private Node findNode(Object target) {
		if (target == null) {
			throw new NullPointerException();
		}

		@SuppressWarnings("unchecked")
		Comparable<? super K> k = (Comparable<? super K>) target;
		int cmp = k.compareTo(p.key);
		// TODO: Fill this in.
		return null;
	}

The parameter target is the key we're looking for. If target is null, findNode throws an exception. Some implementations of Map can handle null as a key, but in a binary search tree, we need to be able to compare keys, so dealing with null is problematic. To keep things simple, we decided that our implementation should not allow null as a key.

The next lines show how we can compare target to a key in the tree. From the signature of get and containsKey, the compiler considers target to be an Object. But we need to be able to compare keys, so we typecast target to Comparable<? super K>, which means that it is comparable to an instance of type K, or any superclass of K.
If you are not familiar with this use of "type wildcards", you can read more here.

Fortunately, dealing with Java's type system is not the point of this exercise. Your job is to fill in the rest of findNode. If it finds a node that contains target as a key, it should return the node. Otherwise it should return null. When you get this working, the tests for get and containsKey should pass.

Note that your solution should only search one path through the tree, so it should take time proportional to the height of the tree. You should not search the whole tree!

Your next task is to fill in containsValue. To get you started, we've provided a helper method, equals, that compares target and a given key. Note that the values in the tree (as opposed to the keys) are not necessarily comparable, so we can't use compareTo; we have to invoke equals on target.

Unlike your previous solution for findNode, your solution for containsValue does have to search the whole tree, so its runtime will proportional to the number of keys, n, not the height of the tree, h.

The next method you should fill in is put. We've provided starter code that handles the simple cases:

	public V put(K key, V value) {
		if (key == null) {
			throw new NullPointerException();
		}
		if (root == null) {
			root = new Node(key, value);
			size++;
			return null;
		}
		return putHelper(root, key, value);
	}

	private V putHelper(Node node, K key, V value) {
		// TODO: Fill this in.
	}

If you try to put null as a key, put throws an exception.

If the tree is empty, put creates a new node and initializes the instance variable root.

Otherwise, it calls putHelper, which is a private method we defined; it is not part of the Map interface.

Fill in putHelper so it searches the tree and:

If key is already in the tree, it replaces the old value with the new, and returns the old value.
If key is not in the tree, it creates a new node, finds the right place to add it, and returns null.

Your implementation of put should take time proportional to h, not n. Ideally you should search the tree only once, but if you find it easier to search twice, you can do that; it will be slower, but it doesn't change the order of growth.

Finally, you should fill in the body of keySet. According to the documentation, this method should return some kind of Set that iterates the keys in order; that is, in increasing order according to the compareTo method. There are several ways to do that, but the simplest is to return an implementation of Set that maintains the order of the elements. The most commonly-used implementations, like HashSet, don't have this property, but Java provides one that does: LinkedHashSet.

We provide an outline of keySet that creates and returns a LinkedHashSet:

	public Set<K> keySet() {
		Set<K> set = new LinkedHashSet<K>();
		return set;
	}

You should finish off this method so it adds the keys from the tree to set in ascending order. Hint: you might want to write a helper method, you might want to make it recursive, and you might want to read about in-order tree traversal.

When you are done, all tests should pass. In the next README, we'll go over our solutions and test the performance of the core methods.

Resources

Binary search tree: Wikipedia.

Type wildcards: Java tutorial.

Tree traversal: Wikipedia.

cjqian/cs-maps-tree-map-lab-codeU