/Coverage_Axis

Primary LanguagePython

Introduction

Official code for the paper Coverage Axis: Inner Point Selection for 3D Shape Skeletonization , Eurographics 2022.

Authors: Zhiyang Dou, Cheng Lin, Rui Xu, Lei Yang, Shiqing Xin, Taku Komura, Wenping Wang.

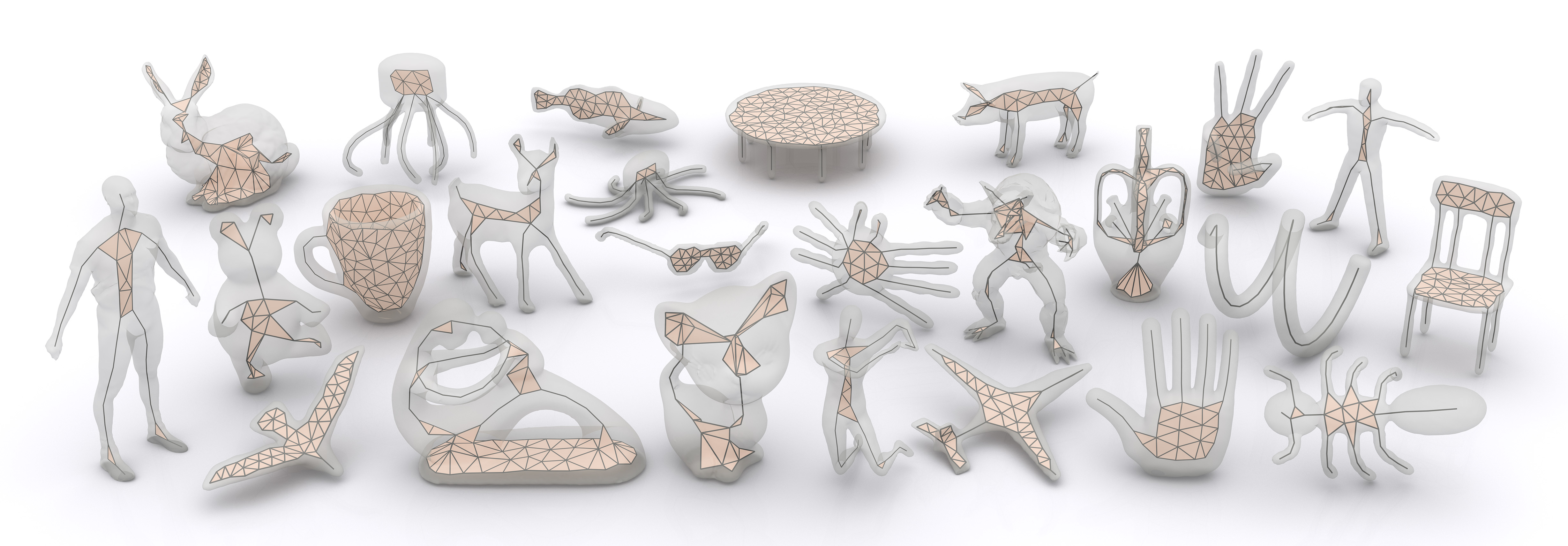teasar In this paper, we present a simple yet effective formulation called Coverage Axis for 3D shape skeletonization. Inspired by the set cover problem, our key idea is to cover all the surface points using as few inside medial balls as possible. This formulation inherently induces a compact and expressive approximation of the Medial Axis Transform (MAT) of a given shape. Different from previous methods that rely on local approximation error, our method allows a global consideration of the overall shape structure, leading to an efficient high-level abstraction and superior robustness to noise. Another appealing aspect of our method is its capability to handle more generalized input such as point clouds and poor-quality meshes. Extensive comparisons and evaluations demonstrate the remarkable effectiveness of our method for generating compact and expressive skeletal representation to approximate the MAT.

This repo contains the code for skeletal point selection by solving SCP.

Key Features

  • Coverage Axis computation for mesh and point cloud inputs.
  • Operations are accelerated by GPU, e.g., computation of coverage matrix and winding number for a mesh.

Requirements

System requirements

  • Linux Ubuntu 20.04
  • Python 3.8
  • Nvidia 3090 (GPU is used for acceleration)

Installation

conda env create -f ca.yml
conda activate CA
pip install -r requirements.txt

Usage

Mesh Input

The input mesh 01Ants-12.off is placed in the folder input. The mesh is normalized.

Specify the settings for Coverage Axis in Coverage_Axis_mesh.py

real_name = '01Ants-12'
surface_sample_num = 2000
dilation = 0.02
inner_points = "voronoi"

Run

python Coverage_Axis_mesh.py

The output is placed in the folder output.

  • inner_points.obj is the candidate inner points.
  • mesh.obj is the input mesh.
  • mesh_samples_2000.obj is the sampled surface points being covered.
  • selected_inner_points.obj is the selected inner points.

Picture

You may use randomly generated points inside the volume as inner candidate points by setting inner_points = "random" . Notably, we already generate a sample. If you choose to produce candidates by randomly sampling inside the shape, it can be a little time consuming. Then run:

python Coverage_Axis_mesh.py

Point Cloud Input

We use Fast Winding Number for Inside-outside determination for point cloud inputs. Please follow this tutorial for building libigl. Note that more dependencies are needed for building libigl:

sudo apt-get install git
sudo apt-get install build-essential
sudo apt-get install cmake
sudo apt-get install libx11-dev
sudo apt-get install mesa-common-dev libgl1-mesa-dev libglu1-mesa-dev
sudo apt-get install libxrandr-dev
sudo apt-get install libxi-dev
sudo apt-get install libxmu-dev
sudo apt-get install libblas-dev
sudo apt-get install libxinerama-dev
sudo apt-get install libxcursor-dev
sudo apt install libeigen3-dev
sudo apt-get install libcgal-dev

git clone https://github.com/libigl/libigl.git
cd libigl/
mkdir build
cd build
cmake ../
make -j4

You need to run cpp codes, you also needs to install Eigen.

Candidate Generation

We generate inside candidates based on Fast Winding Number. The candidates are generated by randomly sampling inside the volume. Other sampling strategies like Voronoi-based sampling can also be used.

More Information

Solve Coverage Axis in MATLAB

The original optimization is solved by MATLAB. In this repo, we solve SCP by Scipy in Python.

f =  ones(1,medial_num); 
A =  -D;
b =  -ones(boundary_num,1)*1;%here ,we fix p_i 
lb = zeros(medial_num,1);
ub = ones(medial_num,1);
iint = [1:medial_num];
tic;
[x,fval]=intlinprog(f,iint,A,b,[],[],lb,ub);
toc;
disp('min_number:');
disp(fval);

References