Graph-Representation

This repo contains experiments related to the representation of combinatorial optimization problems as (heterogeneous) graphs. We include all the code related to the implementations of 4 problem-specific representations, as well as our generic model and our XCSP3 parser.

The problem-specific models are the following:

NeuroSAT : a GNN trained to predict whether a given SAT problem is solvable or not- and an attempt to model SAT problems with a generic graph representation.
TSP-GNN : a GNN trained to predict the decision variant of a TSP.
GC-GNN : a GNN trained to predict the decision variant of a Graph coloring problem.
KS-GNN : a GNN trained to predict the decision variant of a Knapsack problem.

The generic graph representation is intended to be used to model any combinatorial optimization as a graph.

Our heterogeneous graph representation

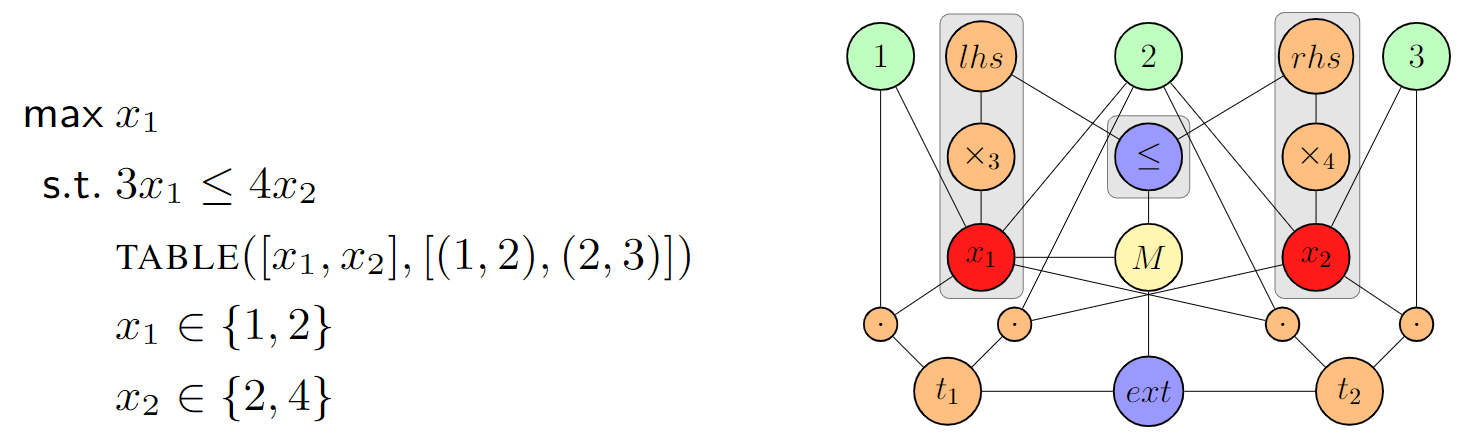
Formally, a combinatorial problem $\mathcal{P}$ is defined as a tuple $\langle X, D(X), C, O \rangle$, where $X$ is the set of variables, $D(X)$ is the set of domains, $C$ is the set of constraints, and $O$ ($X \to \mathbb{R}$) is an objective function. A valid solution is an assignment of each variable to a value of its domain such that every constraint is satisfied. The optimal solution is a valid solution such that no other solution has a better value for the objective.

Our goal is to build a function $\Phi: \langle X, D(X), C, O \rangle \mapsto \mathcal{G}(V,E)$, where $\mathcal{G}$ is a graph and $V$, $E$ are its vertex and arc sets, respectively. We want this function to be injective, i.e., an encoding refers to at most one combinatorial problem. We propose to do so by introducing an encoding consisting in a heterogeneous and undirected graph featuring 5 types of vertices: variables, constraints, values, operators, and model. The core idea is to split each constraint as a sequence of elementary operations, to merge vertices representing the same variable or value, and connect together all the relationships. An illustration of an encoding is proposed in Figure~\ref{fig:encoding}. Intuitively, this process is similar to building the abstract syntax tree of a program. Formally, the encoding gives a graph $$\mathcal{G}(V_{var, cst, val, ope, mod}, f_{var, cst, val, ope, mod}, E)$$ with the five types of vertices, and specific features attached to each vertex. Each type is defined as follows.

Node Types

Values ($V_{val}$)

A value-vertex is introduced for each constant appearing in $\mathcal{P}$. Such values can appear inside either a domain or a constraint. All the values are distinct, i.e., they are represented by a unique vertex. The type of the value (integer, real, etc.) is added as a feature ($f_{val}$) to each value-vertex, using a one-hot encoding.

Variables ($V_{var}$)

A variable-vertex is introduced for each variable appearing in $\mathcal{P}$. A vertex related to a variable $x \in X$ is connected through an edge to each value $v$ inside the domain $D(x)$. Such as the value-vertices, all variables are represented by a unique vertex. The type of the variable (boolean, integer, set, etc.) is added as a feature ($f_{var}$) using a one-hot encoding.

Constraints ($V_{cst}$)

A constraint-vertex is introduced for each constraint appearing in $\mathcal{P}$. A vertex related to a constraint $c \in C$ is connected through an edge to each value $v$ that is present in the constraint. The type of the constraint (inequality, allDifferent, table, etc.) is added as a feature ($f_{cst}$) using a one-hot encoding.

Operators ($V_{ope}$)

Tightly related to constraints, operator-vertices are used to unveil the combinatorial structure of constraints. Operators represent modifications or restrictions on variables involved in constraints (e.g., arithmetic operators, logical operators, views, etc.). An operator-vertex is added each time a variable $x \in X$ is modified by such operations. The vertex is connected to the vertices related to the impacted variables. The type of the operator (+, $\times$, $\land$, $\lor$, etc.) is added as a feature ($f_{ope}$) using a one-hot encoding. If the operator uses a numerical value to modify a variable, this value is used as a feature ($f_{ope}$) as well.

Model ($V_{mod}$)

There is only one model-vertex per graph. This vertex is connected to all constraint-vertices and all variable-vertices involved in the objective function. Its semantics is to gather additional information about the combinatorial problem (e.g., the direction of the optimization) by means of its feature vector ($f_{mod}$).

Example

There are $3$ value-vertices depicted in the encoding the problem above (in green) and $2$ variable-vertices (in red). As $x_1$ contains values $1$ and $2$ in its domain, they are connected with an edge, and similarly for the domain of $x_2$. There are $2$ constraint-vertices (in blue), one for the inequality ($\leq$) and one for the table constraint ($\textsf{ext}$). The gray area in the figure shows how the constraint $3x_1 \leq 4x_2$ is scattered with operators (in orange). Specifically, it involves a multiplication ($\times$, with feature $3$) of $x_1$ on the right-side ($\textsf{rhs}$) and a multiplication ($\times$, with feature $4$) of $x_2$ on the left-side ($\textsf{lhs}$). The outer operators are then connected to the related constraint, e.g., $\textsf{rhs}$ and $\textsf{lhs}$ for the inequality ($\leq$). The constraint $table([x_1,x_2],[(1,2),(2,3)])$ is expressed in a similar way. It involves two tuples $t_1$ and $t_2$. Finally, the model-vertex (in yellow) is connected to the two constraints, and to variable $x_1$, as it is part of the objective function.

Structure

The repo is structured as follows:

src
├── __init__.py
├── generic_xcsp
│   ├── __init__.py
│   ├── alldifferent.py
│   ├── constraints
│   ├── constraints.py
│   ├── dataset.py
│   ├── element.py
│   ├── generic_model.py
│   ├── graph_builder.py
│   ├── instance.py
│   ├── intension_utils.py
│   ├── sum_constraint.py
│   ├── training_config.py
│   └── variable_parsing.py
├── models
│   ├── __init__.py
│   ├── common
│   │   ├── __init__.py
│   │   ├── config.py
│   │   ├── lstm_conv.py
│   │   ├── pytorch_lr_scheduler.py
│   │   ├── pytorch_models.py
│   │   ├── pytorch_utilities.py
│   │   └── training_utils.py
│   ├── decision_tsp
│   │   ├── __init__.py
│   │   ├── base_model.py
│   │   ├── config.py
│   │   ├── dataset.py
│   │   ├── generic_model.py
│   │   ├── instance_generator.py
│   │   ├── instance_parser.py
│   │   ├── plotting_utils.py
│   │   ├── setup.md
│   │   ├── xml_element_generator.py
│   │   └── xml_extension_generator.py
│   ├── graph_coloring
│   │   ├── __init__.py
│   │   ├── base_model.py
│   │   ├── config.py
│   │   ├── dataset.py
│   │   ├── gc_parser.py
│   │   ├── graph_coloring_instances
│   │   ├── instance_generator.py
│   │   ├── rename_graphs.py
│   │   └── xml_generator.py
│   ├── knapsack
│   │   ├── instance_generator.py
│   │   └── knapsack_model.py
│   └── sat
│       ├── __init__.py
│       ├── config.py
│       ├── dataset.py
│       ├── neurosat_model.py
│       ├── plotting_utils.py
│       ├── sat_parser.py
│       ├── scripts
│       │   ├── PyMiniSolvers
│       │   ├── gen_sr_dimacs.py
│       │   ├── generate_data.sh
│       │   └── setup.sh
├── build_marty_et_al_datasets.py
├── requirements.txt
├── test_generic_model.py
├── test_graph_coloring.py
├── test_knapsack_specific_model.py
├── test_sat.py
├── test_tsp.py
├── train_generic_model.py
├── train_graph_coloring.py
├── train_knapsack_specific_model.py
├── train_sat.py
├── train_tsp.py
└── utils
    └── lzma_utils.py

The src/models subdirectory contains problem-specific models, instance generators and related utilities, while the generic stuff in in the src/generic_xcsp subdirectory. The src/utils subdirectory contains utilities for compressing and decompressing lzma files.

Setup

As usual, start by creating a virtual environment and installing the requirements. We will describe the setup to generate data for all different problems. Please note that, for the problem-specific models, as well as the generic models, you will need 2 directories to store your data: raw and processed. The raw directory will contain the raw data, while the processed directory will contain the data after it has been processed and converted to PyTorch-Geometric objects.

SAT

The SAT model and instance generator are based on the NeuroSAT. To complete the setup, cd into src/models/sat and run setup.sh. To generate instances, cd into src/models/sat and run ./generate_data.sh.

TSP

The TSP instance generator setup is a little tedious. It uses pyconcorde - a pytorch wrapper for the concorde TSP solver. The setup is described in the following section.

QSopt

Concorde requires a linear programming solver. In this setup, we use QSopt. Simply download it (all three files) from (this link)[https://www.math.uwaterloo.ca/~bico/qsopt/downloads/downloads.htm]. I am using ubuntu, so I download all 3 files located at the bottom of the page and I place them in a directory named qsopt_solver.

Concorde Download, Installation and Setup

sudo apt update
sudo apt install build-essential libgmp-dev libgsl-dev
wget http://www.math.uwaterloo.ca/tsp/concorde/downloads/codes/src/co031219.tgz
tar -xvf co031219.tgz
cd concorde
./configure --prefix=/usr/local --with-qsopt=[full_path_to_qsopt_solver_directory]
make
export PATH="/usr/local/concorde/TSP:$PATH

Adjust the last line according to where you downloaded the concorde solver. Following this step by step will allow you to use concorde. This can be tested by running the following command:

concorde -s 99 -k 100

Running this command should yield the following:

concorde -s 99 -k 100
Host: [host_name]  Current process id: xxxx
Using random seed 99
Random 100 point set
XSet initial upperbound to 780 (from tour)
  LP Value  1: 738.500000  (0.00 seconds)
  LP Value  2: 765.000000  (0.02 seconds)
  LP Value  3: 774.660000  (0.05 seconds)
  LP Value  4: 778.000000  (0.09 seconds)
  LP Value  5: 778.465517  (0.13 seconds)
  LP Value  6: 778.705882  (0.16 seconds)
  LP Value  7: 779.538462  (0.20 seconds)
  LP Value  8: 779.937500  (0.24 seconds)
  LP Value  9: 780.000000  (0.26 seconds)
New lower bound: 780.000000
Final lower bound 780.000000, upper bound 780.000000
Exact lower bound: 780.000000
DIFF: 0.000000
Final LP has 180 rows, 336 columns, 2921 nonzeros
Optimal Solution: 780.00
Number of bbnodes: 1
Total Running Time: 0.45 (seconds)

Installing pyconcorde

pyconcorde is a python wrapper for the concorde TSP solver. It can be installed by running the following commands:

git clone https://github.com/jvkersch/pyconcorde
cd pyconcorde
pip install -e .

Once the setup is complete, cd into src/models/decision_tsp and run python3 instance_generator.py.

Graph Coloring

The data generation for the graph coloring problem is straightforward. Simply cd into src/models/graph_coloring and run python3 instance_generator.py.

Knapsack

The data generation for the knapsack problem is straightforward. Simply cd into src/models/knapsack and run python3 instance_generator.py.

Generic Models

The generic raw data is created from the original raw data. For each problem, a data generator is provided. It is slightly different for all problems.

SAT

Both generic and specific SAT instances are created directly from DIMACS files. The generic data is created by setting generic_representation to True in the training script.

TSP-Element

To generate TSP-Element instances, cd into src/models/decision_tsp and run python3 xml_element_generator.py. This will generate the raw data.

TSP-Extension

To generate TSP-Element instances, cd into src/models/decision_tsp and run python3 xml_extension_generator.py. This will generate the raw data.

Graph Coloring

To generate graph coloring instances, cd into src/models/graph_coloring and run python3 xml_generator.py. This will generate the raw data.

Knapsack

Knapsack are generated directly as XML files.

Training

Training scripts are provided for all models. They are located in the src directory. The training scripts are named as follows:

train_sat.py Trains either a SAT-specific or a generic model
train_tsp.py Trains a TSP-specific model
train_graph_coloring.py Trains a graph coloring-specific model
train_knapsack_specific_model.py Trains a knapsack-specific model
train_generic_model.py Trains a generic model

corail-research/learning-generic-csp

Graph-Representation

Our heterogeneous graph representation

Node Types

Values ($V_{val}$)

Variables ($V_{var}$)

Constraints ($V_{cst}$)

Operators ($V_{ope}$)

Model ($V_{mod}$)

Example

Structure

Setup

SAT

TSP

QSopt

Concorde Download, Installation and Setup

Installing pyconcorde

Graph Coloring

Knapsack

Generic Models

SAT

TSP-Element

TSP-Extension

Graph Coloring

Knapsack

Training