My Solution

Minified: 363 chars (conways_game_of_life.py)

from itertools import product
def c(p, r):
  for i in range(r + 1):
    if not p:  # Empty world
      return []
    d = min(p, key=lambda t: t[0])[0]  # x_min
    e = min(p, key=lambda t: t[1])[1]  # y_min
    p = [(x-d, y-e) for (x, y) in p]  # Normalize p
    if i == r:
      break
    a = max(p, key=lambda t: t[0])[0]  # x_max
    b = max(p, key=lambda t: t[1])[1]  # y_max
    p = [
      (x, y) # Test all points in between min and max x/y coords, aswell as an extra row/column on each side
      for x in range(-1, b+2)
      for y in range(-1, a+2)
      # Shift 0b1000 (if cell is alive: 0b11000) by number of alive surrounding cells right,
      # if cell is alive in next round LSB is 1
      if (
             8 + 16 * ((x, y) in p)
             >>
             sum((x+x_, y+y_) in p for (x_, y_) in product([-1, 0, 1], repeat=2))
         ) & 1
    ]

  return p

Conway's Game of Life

Code Golf Challenge für den IT Carreer Summit

Gewinne eine RTX 3070 TI und vieles mehr

Was ist die Aufgabe

Eure Aufgabe ist es, Conways Game of Life zu implementieren. Frei kopiert von Wikipedia: "Das Spiel des Lebens (englisch Conway’s Game of Life) ist ein vom Mathematiker John Horton Conway 1970 entworfenes Spiel, basierend auf einem zweidimensionalen zellulären Automaten. Es ist eine einfache und bis heute populäre Umsetzung der Automaten-Theorie von Stanisław Marcin Ulam."

Wie teilnehmen?

Ladet euch von diesem Repository die Dateien main.py und conways_game_of_life.py herunter
Fügt euren Code in conways_game_of_life.py ein
Startet die main.py mit sowas wie python main.py --coords 1,2 3,4 5,6 --rounds 2
- --coords gibt die Koordinaten x,y der lebenden Punkte an. Getrennt wird mit einem Leerzeichen zwischen den Punkten und einem Komma zwischen den Koordinaten. Es ist alles 2-dimensional.
- --rounds gibt die Anzahl der Runden an, die ihr simulieren sollt
Minimiert den Code
- Wir spielen Code Golf. Hier gewinnt, wer den kürzesten, korrekten Code abliefern kann.
- Bei Gleichstand gewinnt die durchschnittliche Laufzeit für dieselbe Aufgabe auf meinem Rechner.
Sendet eure conways_game_of_life.py (AUSSCHLIEßLICH DIE!) an diese Adresse und packt euren Namen von Clabb.io dazu! Sonst können wir euch am Ende nicht identifizieren.
Ihr habt Zeit bis 14:59 einschließlich. Ab 15:00 wird nichts mehr angenommen.
Die Siegerehrung findet 15:30 HIER statt.

Wie funktioniert Conways Game of Life?

Das wird hier sehr gut erklärt: Es gibt tote und lebende Zellen. Zellen sind immer viereckig und haben damit 8 direkte Nachbarn, links, rechts, oben, unten und die 4 Diagonalen. Es wird in Runden gedacht.

Die toten Zellen fangen in der nächsten Runde an zu leben, wenn in ihrem direkten Umfeld exakt 3 andere Zellen leben.
Die lebenden Zellen sterben in der nächsten Runde an Einsamkeit, wenn weniger als 2 Zellen in ihrem Umfeld leben, also 1 oder 0.
Die lebenden Zellen sterben in der nächsten Runde an Überbevölkerung, wenn mehr als 3 Zellen in ihrem Umfeld leben.
Befinden sich 2 oder 3 lebende Zellen im Umfeld der Zelle, bleibt sie in der nächsten Runde am leben.

Die Zelle selbst wird nicht mit eingerechnet. Eine neue Runde berechnet sich für alle Zellen immer gleichzeitig. Eine Visualisierung des Game of Life gibt es hier.

Normalisierung

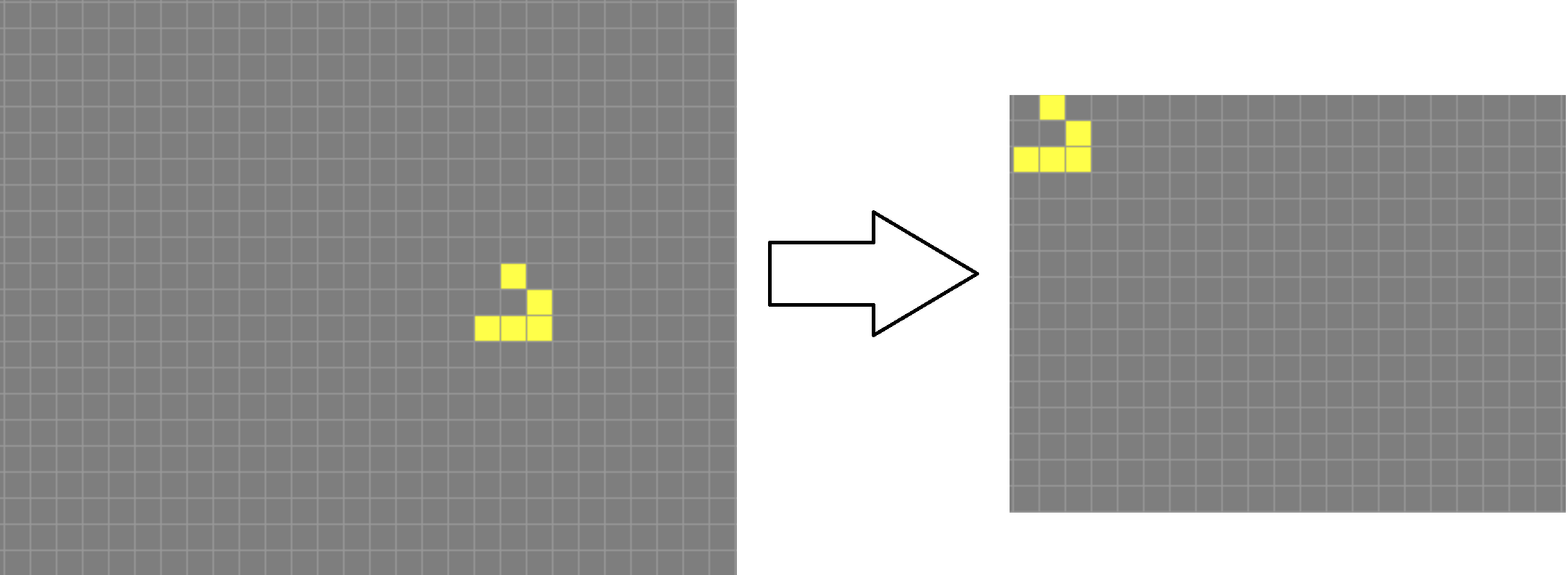
Bei Conways Game of Life kann es zu "Wanderungen" kommen. Das heißt, sind am Anfang Felder 0,0; 1,0 und 0,1 belegt könnte irgendwann später Feld 1000,1337; 1001,1337 etc belegt sein, jedoch im Bereich 0,0 ist nichts mehr aktiv. Auch in die andere Richtung kann es sich ausbreiten, also mit aktiven Feldern zB auf -10,-20. Für die Lösung MÜSSEN die Ergebnisse normalisiert sein. Für Listen kann es ja keine negativen Einträge geben. Das bedeutet:

Ist die Zeile unter 0,x leer, sprich keine einzige Zelle am Leben muss sie gelöscht werden, sodass 1,x zu 0,x wird. Ist 1,x auch leer muss die Zelle ebenfalls gelöscht werden.
Dasselbe gilt für die Spalte x,0. Auch hier muss x,0 gelöscht werden, wenn keine Zelle dort lebt und x,1 muss an x,0 rücken.
Sollte die Zelle an -1,x oder x,-1 zum Leben erwachen muss ebenfalls geschoben werden, dieses Mal in die positive Richtung
Falls es unverständlich war: Es sollte in der obersten Zeile irgendwo eine Zelle leben und in der linkesten Spalte muss auch eine Zelle leben. Negative Indices gehen natürlich ebenfalls nicht

Q&A

Wo kann ich Fragen stellen?

[Hier anfragen.](mailto:kontakt@the-morpheus.de) dann wird es in diesem Readme eingetragen.

Welche Libraries sind erlaubt?

Standard-Library plus Numpy und Pandas.

Muss die Ausgabe sortiert sein?

Nein. Sie muss nur der Form Liste von Tuples folgen.

Müssen alle Runden ausgegeben werden?

Nein. Nur die allerletzte Runde.

Tabs?

ÄNDERUNG: Zählen doch als 1 Zeichen. Ich wurde darauf aufmerksam gemacht, dass es ja keinen Unterschied macht und man ja auch mit einem Leerzeichen einrücken kann.

Fehlerhafte Eingaben

Wenn es in der Main.py zu einem Fehler führt, ist das für euch egal, es wäre aber möglich "None"-Koordinaten zu bekommen. Die müsst ihr abfangen. Beispiel: Der Aufruf "python main.py --coords 1,None --rounds 2" führt zu einem Fehler in der main.py, ist daher für euch egal. Beispiel 2: 'python main.py --rounds 2' führt zu coords = None und muss von euch abgedeckt werden - es leben dann einfach keine Zellen.

Input normalisiert?

Nein, nicht unbedingt. Es könnte jegliche Zahl als Eingabe kommen.

Negative und 0-Runden

Negative Runden existieren nicht und sind nicht erlaubt. Ihr müsst sie nicht behandeln. Wenn Rounds = 0 übergeben wird, heißt das, dass keine Epoche stattfindet, die (gegebenenfalls zu normalisierende) Anfangskonstellation ist also die Ausgabe.

Leere / Tote Welten

Sind absolut legitim und kommen häufig vor. Gebt eine leere Liste oder None zurück. Beides ist erlaubt.

Maximale Runden

Stellt sicher, dass es bis zu 10.000 Runden funktioniert.

Doppelte Eingaben

Werden nicht(!) stattfinden, dh ihr dürft davon ausgehen, dass 1,1 1,1 niemals euch gegeben wird.

cornzz/ITCS_Conways_Challenge