-
$\mu$ : scalar mean rating -
$b_i$ : scalar bias term for user$i$ -
$c_j$ : scalar bias term for movie$j$ -
$u_i$ : K-dimensional vector for user$i$ -
$v_j$ : K-dimensional vector for movie$j$
- We can construct a weighted undirect graph from a given pair of user and movie, and weight will be rating given to movie by user.
- we can construct this matrix like
$A[i][j]=r_{ij}$ here$i$ is user_id,$j$ is movie_id and$r_{ij}$ is rating given by user$i$ to the movie$j$
We will Apply SVD decomposition on the Adjaceny matrix
if
-
Matrix
$U$ can be represented as matrix representation of users, where each row$u_{i}$ represents a k-dimensional vector for a user -
Matrix
$V$ can be represented as matrix representation of movies, where each row$v_{j}$ represents a k-dimensional vector for a movie.
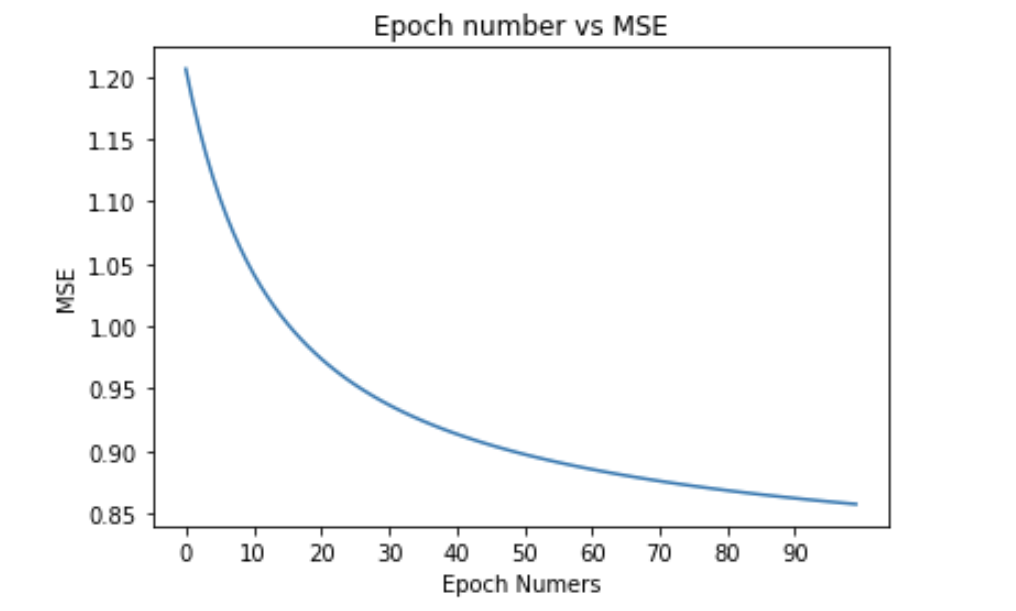
for each epoch:
for each pair of (user, movie):
b_i = b_i - learning_rate * dL/db_i
c_j = c_j - learning_rate * dL/dc_j
predict the ratings with formula