Fast, memory efficient Multiple Imputation by Chained Equations (MICE) with random forests. It can impute categorical and numeric data without much setup, and has an array of diagnostic plots available. The R version of this package may be found here.
This document contains a thorough walkthrough of the package, benchmarks, and an introduction to multiple imputation. More information on MICE can be found in Stef van Buuren’s excellent online book, which you can find here.
miceforest has 4 main classes which the user will interact with:
KernelDataSet- a kernel data set is a dataset on which the mice algorithm is performed. Models are saved inside the instance, which can also be called on to impute new data. Several plotting methods are included to run diagnostics on the imputed data.MultipleImputedKernel- a collection ofKernelDataSets. Has additional methods for accessing and comparing multiple kernel datasets together.ImputedDataSet- a single dataset that has been imputed. These are returned afterimpute_new_data()is called.MultipleImputedDataSet- A collection of datasets that have been imputed. Has additional methods for comparing the imputations between datasets.
You can download the latest stable version from PyPi:
$ pip install miceforestYou can also download the latest development version from this repository:
$ pip install git+https://github.com/AnotherSamWilson/miceforest.gitIn these examples we will be looking at a few simple examples of imputation. We need to load the packages, and define the data:
import miceforest as mf
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
# Load data and introduce missing values
iris = pd.concat(load_iris(as_frame=True,return_X_y=True),axis=1)
iris['target'] = iris['target'].astype('category')
iris_amp = mf.ampute_data(iris,perc=0.25,random_state=1991)If you only want to create a single imputed dataset, you can use
KernelDataSet:
# Create kernel.
kds = mf.KernelDataSet(
iris_amp,
save_all_iterations=True,
random_state=1991
)
# Run the MICE algorithm for 3 iterations
kds.mice(3)
# Return the completed kernel data
completed_data = kds.complete_data()There are also an array of plotting functions available, these are discussed below in the section Diagnostic Plotting. The plotting behavior between single imputed datasets and multi-imputed datasets is slightly different.
We can also create a class which contains multiple KernelDataSets,
along with easy ways to compare them:
# Create kernel.
kernel = mf.MultipleImputedKernel(
iris_amp,
datasets=4,
save_all_iterations=True,
random_state=1991
)
# Run the MICE algorithm for 3 iterations on each of the datasets
kernel.mice(3)Printing the MultipleImputedKernel object will tell you some high
level information:
print(kernel)## Class: MultipleImputedKernel
## Models Saved: Last Iteration
## Datasets: 4
## Iterations: 3
## Imputed Variables: 5
## save_all_iterations: True
A very nice thing about random forests is that they are trivially
parallelizable. We can save a lot of time by setting the n_jobs
parameter in both the fit and predict methods for the random forests:
# Run the MICE algorithm for 2 more iterations on the kernel,
kernel.mice(2,n_jobs=2)Any other arguments may be passed to either class
(RandomForestClassifier,RandomForestRegressor). In our example, we
may not have saved much (if any) time. This is because there is overhead
with using multiple cores, and our data is very small.
It is possible to customize our imputation procedure by variable. By
passing a named list to variable_schema, you can specify the
predictors for each variable to impute. You can also select which
variables should be imputed using mean matching, as well as the mean
matching candidates, by passing a dict tomean_match_candidates:
var_sch = {
'sepal width (cm)': ['target','petal width (cm)'],
'petal width (cm)': ['target','sepal length (cm)']
}
var_mmc = {
'sepal width (cm)': 5,
'petal width (cm)': 0
}
cust_kernel = mf.MultipleImputedKernel(
iris_amp,
datasets=3,
variable_schema=var_sch,
mean_match_candidates=var_mmc
)
cust_kernel.mice(2)Multiple Imputation can take a long time. If you wish to impute a
dataset using the MICE algorithm, but don’t have time to train new
models, it is possible to impute new datasets using a
MultipleImputedKernel object. The impute_new_data() function uses
the random forests collected by MultipleImputedKernel to perform
multiple imputation without updating the random forest at each
iteration:
# Our 'new data' is just the first 15 rows of iris_amp
new_data = iris_amp.iloc[range(15)]
new_data_imputed = kernel.impute_new_data(new_data=new_data)
print(new_data_imputed)## Class: MultipleImputedDataSet
## Datasets: 4
## Iterations: 5
## Imputed Variables: 5
## save_all_iterations: False
All of the imputation parameters (variable_schema,
mean_match_candidates, etc) will be carried over from the original
MultipleImputedKernel object. When mean matching, the candidate values
are pulled from the original kernel dataset. To impute new data, the
save_models parameter in MultipleImputedKernel must be > 0. If
save_models == 1, the model from the latest iteration is saved for
each variable. If save_models > 1, the model from each iteration is
saved. This allows for new data to be imputed in a more similar fashion
to the original mice procedure.
As of now, miceforest has four diagnostic plots available.
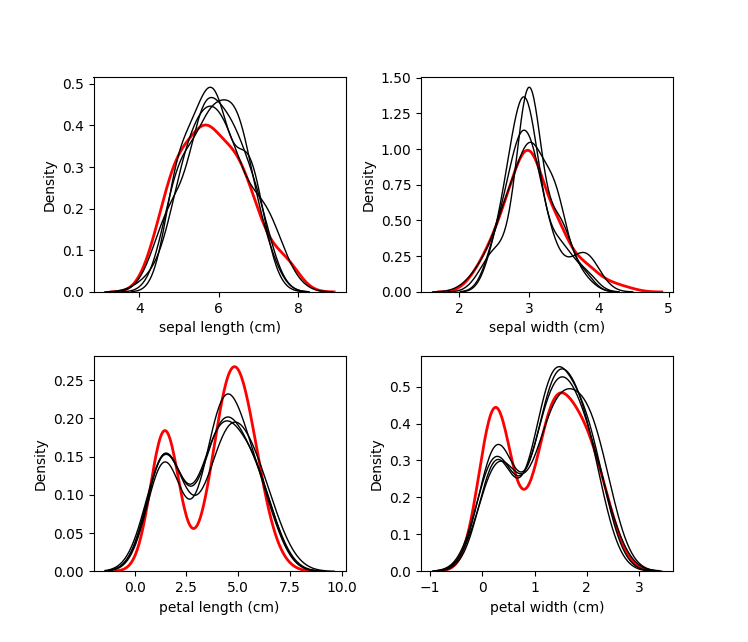
We probably want to know how the imputed values are distributed. We can
plot the original distribution beside the imputed distributions in each
dataset by using the plot_imputed_distributions method of an
MultipleImputedKernel object:
kernel.plot_imputed_distributions(wspace=0.3,hspace=0.3)The red line is the original data, and each black line are the imputed values of each dataset.
We are probably interested in knowing how our values between datasets
converged over the iterations. The plot_correlations method shows you
a boxplot of the correlations between imputed values in every
combination of datasets, at each iteration. This allows you to see how
correlated the imputations are between datasets, as well as the
convergence over iterations:
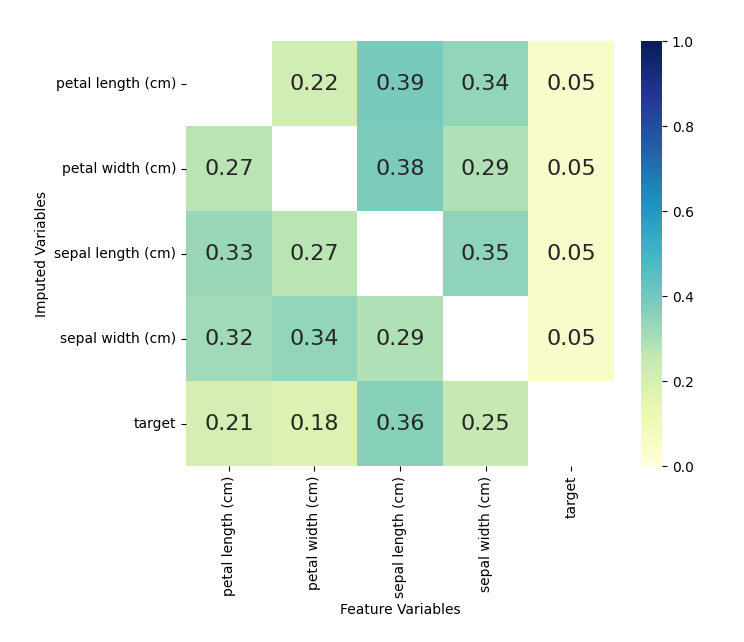
kernel.plot_correlations()We also may be interested in which variables were used to impute each
variable. We can plot this information by using the
plot_feature_importance method.
kernel.plot_feature_importance(annot=True,cmap="YlGnBu",vmin=0, vmax=1)The numbers shown are returned from the sklearn random forest
_feature_importance attribute. Each square represents the importance
of the column variable in imputing the row variable.
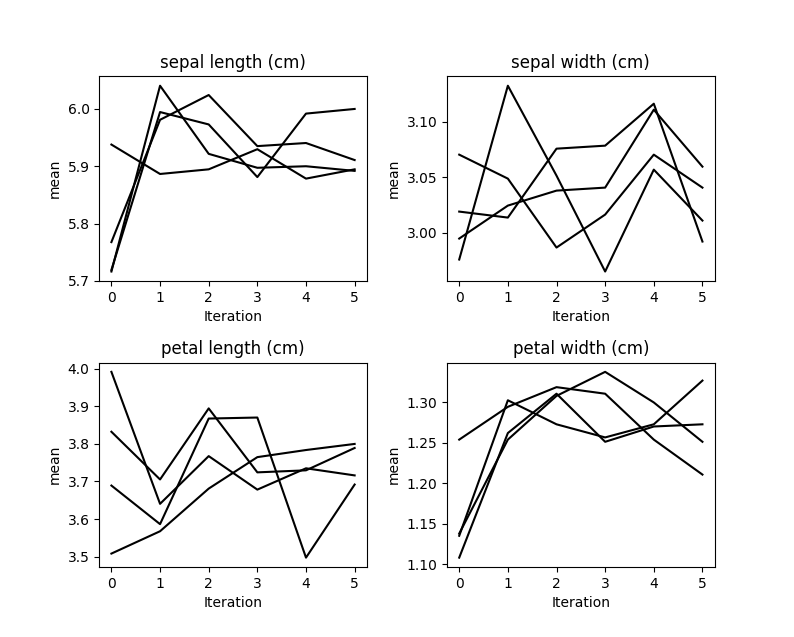
If our data is not missing completely at random, we may see that it takes a few iterations for our models to get the distribution of imputations right. We can plot the average value of our imputations to see if this is occurring:
kernel.plot_mean_convergence(wspace=0.3, hspace=0.4)Our data was missing completely at random, so we don’t see any convergence occurring here.
To return the imputed data simply use the complete_data method:
dataset_1 = kernel.complete_data(0)This will return a single specified dataset. Multiple datasets are typically created so that some measure of confidence around each prediction can be created.
Since we know what the original data looked like, we can cheat and see how well the imputations compare to the original data:
acclist = []
for iteration in range(kernel.iteration_count()+1):
target_na_count = kernel.na_counts['target']
compdat = kernel.complete_data(dataset=0,iteration=iteration)
# Record the accuract of the imputations of target.
acclist.append(
round(1-sum(compdat['target'] != iris['target'])/target_na_count,2)
)
# acclist shows the accuracy of the imputations
# over the iterations.
print(acclist)## [0.32, 0.76, 0.78, 0.81, 0.86, 0.86]
In this instance, we went from a ~32% accuracy (which is expected with
random sampling) to an accuracy of ~86%. We managed to replace the
missing target values with a pretty high degree of accuracy!
Multiple Imputation by Chained Equations ‘fills in’ (imputes) missing data in a dataset through an iterative series of predictive models. In each iteration, each specified variable in the dataset is imputed using the other variables in the dataset. These iterations should be run until it appears that convergence has been met.
This process is continued until all specified variables have been imputed. Additional iterations can be run if it appears that the average imputed values have not converged, although no more than 5 iterations are usually necessary.
MICE is particularly useful if missing values are associated with the target variable in a way that introduces leakage. For instance, let’s say you wanted to model customer retention at the time of sign up. A certain variable is collected at sign up or 1 month after sign up. The absence of that variable is a data leak, since it tells you that the customer did not retain for 1 month.
Information is often collected at different stages of a ‘funnel’. MICE can be used to make educated guesses about the characteristics of entities at different points in a funnel.
MICE can be used to impute missing values, however it is important to keep in mind that these imputed values are a prediction. Creating multiple datasets with different imputed values allows you to do two types of inference:
- Imputed Value Distribution: A profile can be built for each imputed value, allowing you to make statements about the likely distribution of that value.
- Model Prediction Distribution: With multiple datasets, you can build multiple models and create a distribution of predictions for each sample. Those samples with imputed values which were not able to be imputed with much confidence would have a larger variance in their predictions.
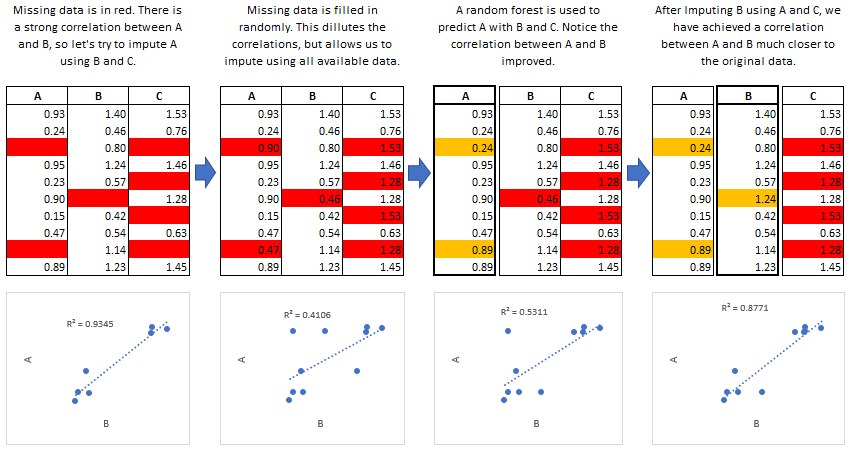
miceforest can make use of a procedure called predictive mean matching
(PMM) to select which values are imputed. PMM involves selecting a
datapoint from the original, nonmissing data which has a predicted value
close to the predicted value of the missing sample. The closest N
(mean_match_candidates parameter) values are chosen as candidates,
from which a value is chosen at random. This can be specified on a
column-by-column basis. Going into more detail from our example above,
we see how this works in practice:
This method is very useful if you have a variable which needs imputing which has any of the following characteristics:
- Multimodal
- Integer
- Skewed
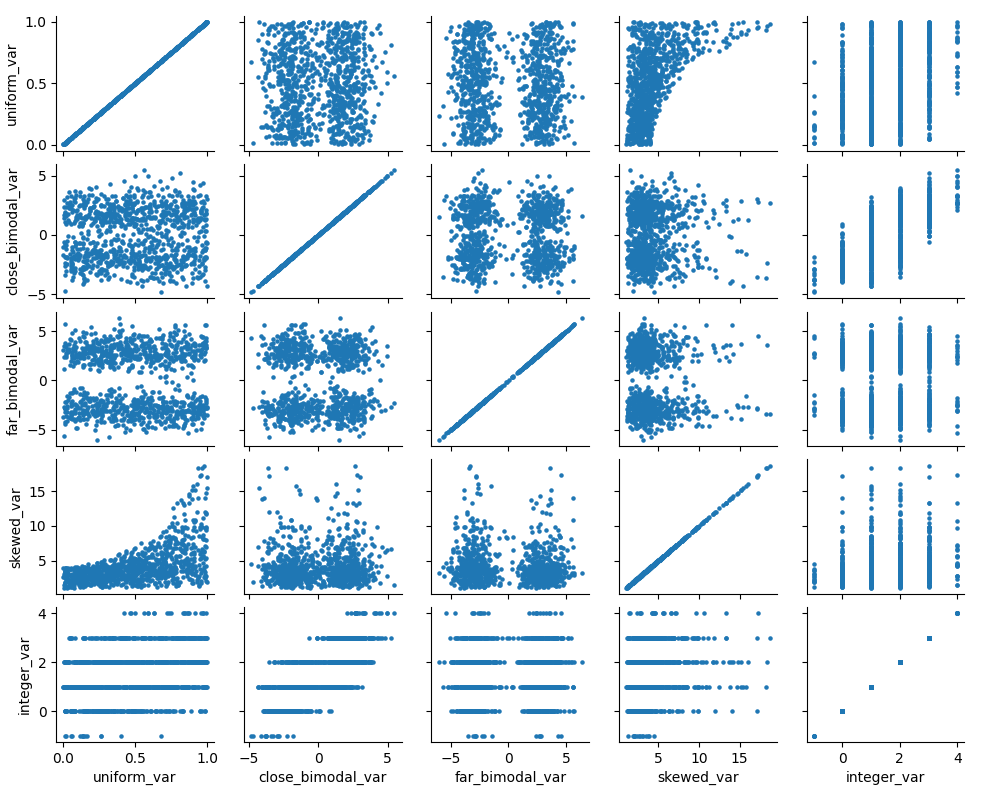
As an example, let’s construct a dataset with some of the above characteristics:
randst = np.random.RandomState(1991)
# random uniform variable
nrws = 1000
uniform_vec = randst.uniform(size=nrws)
def make_bimodal(mean1,mean2,size):
bimodal_1 = randst.normal(size=nrws, loc=mean1)
bimodal_2 = randst.normal(size=nrws, loc=mean2)
bimdvec = []
for i in range(size):
bimdvec.append(randst.choice([bimodal_1[i], bimodal_2[i]]))
return np.array(bimdvec)
# Make 2 Bimodal Variables
close_bimodal_vec = make_bimodal(2,-2,nrws)
far_bimodal_vec = make_bimodal(3,-3,nrws)
# Highly skewed variable correlated with Uniform_Variable
skewed_vec = np.exp(uniform_vec*randst.uniform(size=nrws)*3) + randst.uniform(size=nrws)*3
# Integer variable correlated with Close_Bimodal_Variable and Uniform_Variable
integer_vec = np.round(uniform_vec + close_bimodal_vec/3 + randst.uniform(size=nrws)*2)
# Make a DataFrame
dat = pd.DataFrame(
{
'uniform_var':uniform_vec,
'close_bimodal_var':close_bimodal_vec,
'far_bimodal_var':far_bimodal_vec,
'skewed_var':skewed_vec,
'integer_var':integer_vec
}
)
# Ampute the data.
ampdat = mf.ampute_data(dat,perc=0.25,random_state=randst)
# Plot the original data
import seaborn as sns
import matplotlib.pyplot as plt
g = sns.PairGrid(dat)
g.map(plt.scatter,s=5)kernelmeanmatch <- mf.MultipleImputedKernel(ampdat,mean_match_candidates=5)
kernelmodeloutput <- mf.MultipleImputedKernel(ampdat,mean_match_candidates=0)
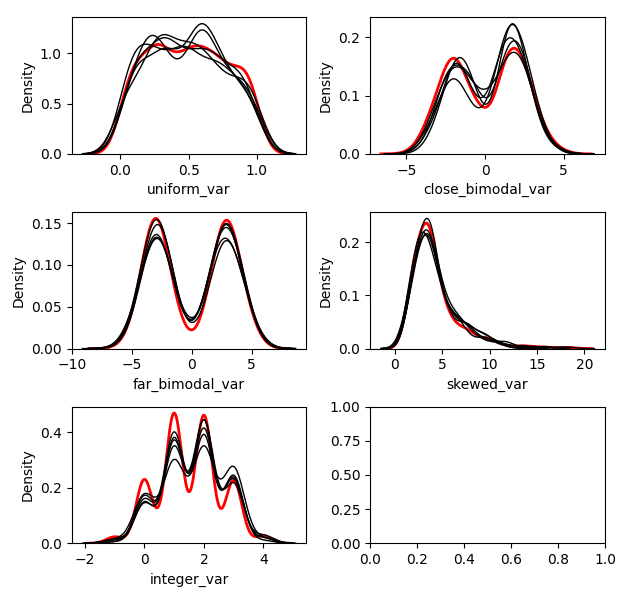
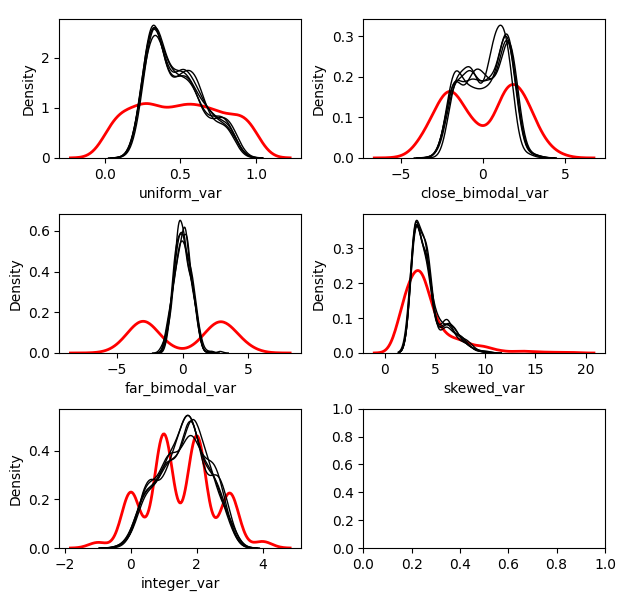
kernelmeanmatch.mice(5)
kernelmodeloutput.mice(5)Let’s look at the effect on the different variables.
kernelmeanmatch.plot_imputed_distributions(wspace=0.2,hspace=0.4)kernelmodeloutput.plot_imputed_distributions(wspace=0.2,hspace=0.4)You can see the effects that mean matching has, depending on the distribution of the data. Simply returning the value from the model prediction, while it may provide a better ‘fit’, will not provide imputations with a similair distribution to the original. This may be beneficial, depending on your goal.