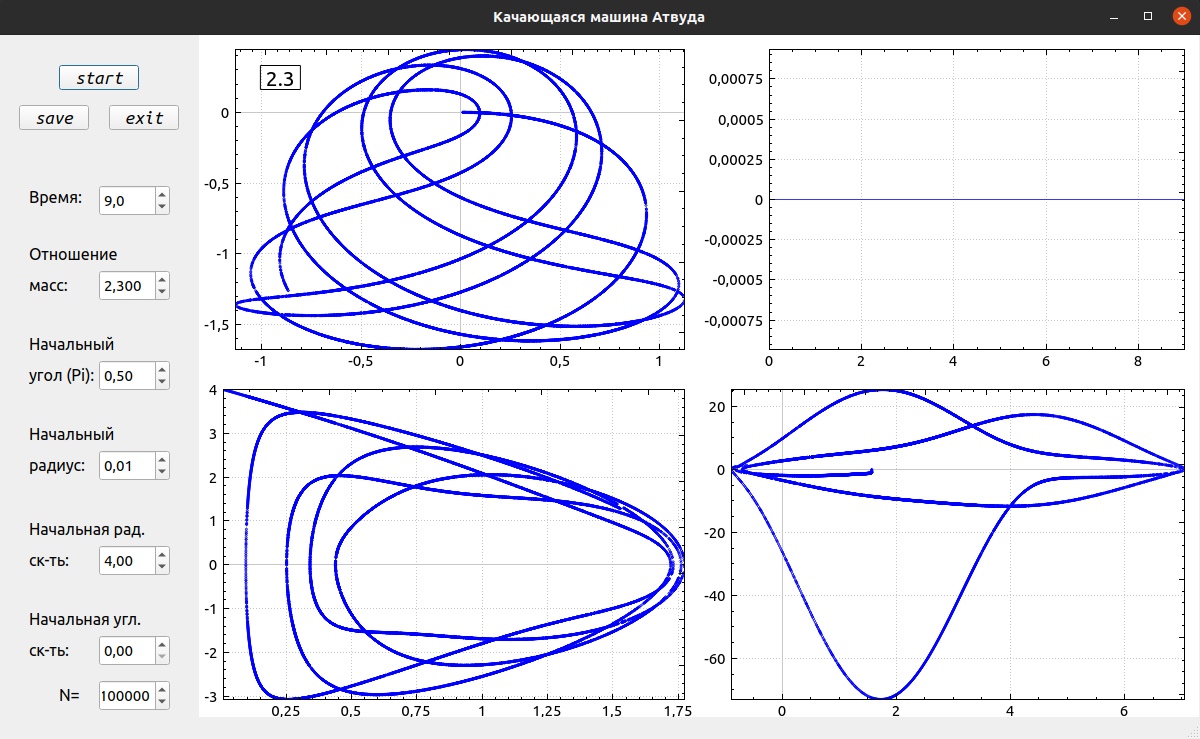
This project numerically solves the system of differential equations describing a swinging Atwood machine using the Runge-Kutta method of the 4th order. The program provides a graphical interface where you can set up the parameters and view the resulting trajectory path:
Parameters that can be set in the program menu:
- Number of steps;
- Simulation time;
- Mass ratio of the weights;
- Initial angle;
- Initial string length;
- Initial radial velocity;
- Initial angular velocity;
Graphs generated by the program:
- Trajectory of the weight (top left);
- Relative energy change
$\epsilon(t)=|100*\frac{E(t)-E(0)}{E(0)}|$ over time$t$ (top right); - Phase portrait #1: dependence of
$\dot r(t)$ on$r(t)$ (bottom left); - Phase portrait #2: dependence of
$\dot \theta (t)$ on$\theta (t)$ (bottom right);
- cpp_qt_project: Contains the C++ code for the Qt project.
- pictures: Contains the trajectory plots generated from the calculations. The filenames follow the format:
MassRatio_StartingAngle.png. - project_overview_RU.pdf: A detailed description of the project in PDF format (in Russian).
- atwood.nb: Additional code written in Wolfram Mathematica. This code solves the problem using the built-in
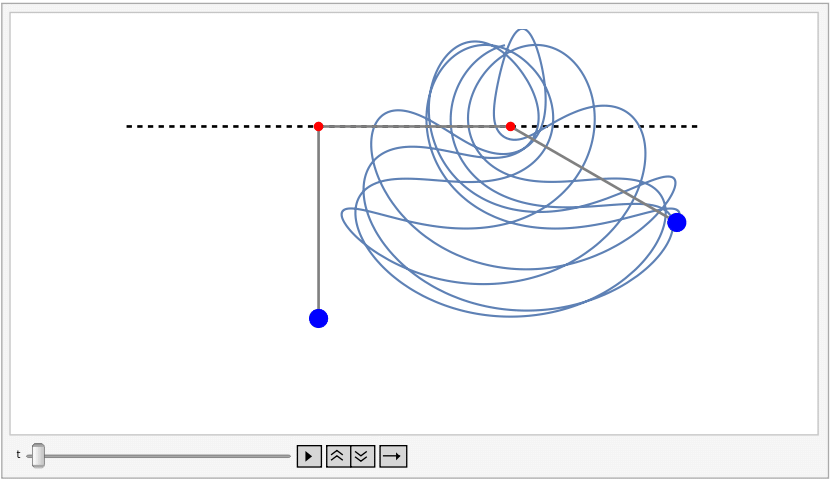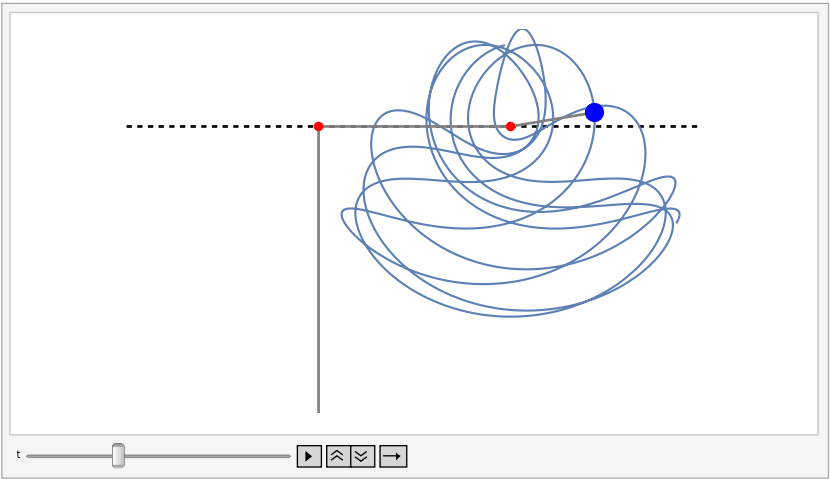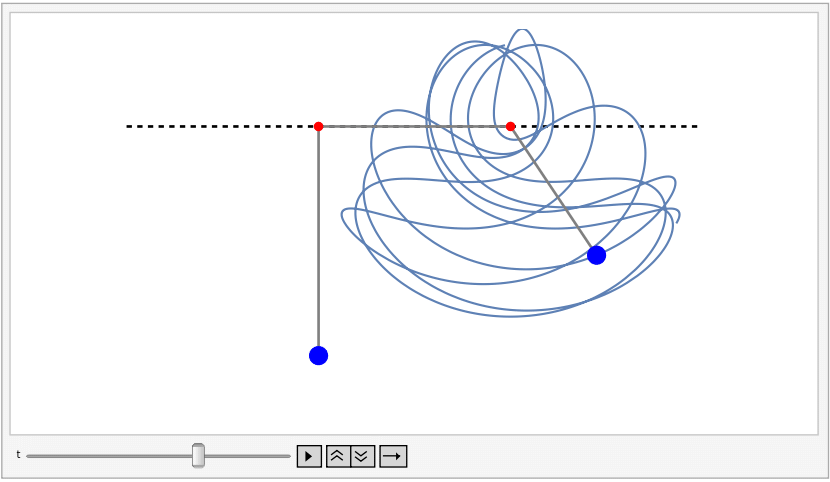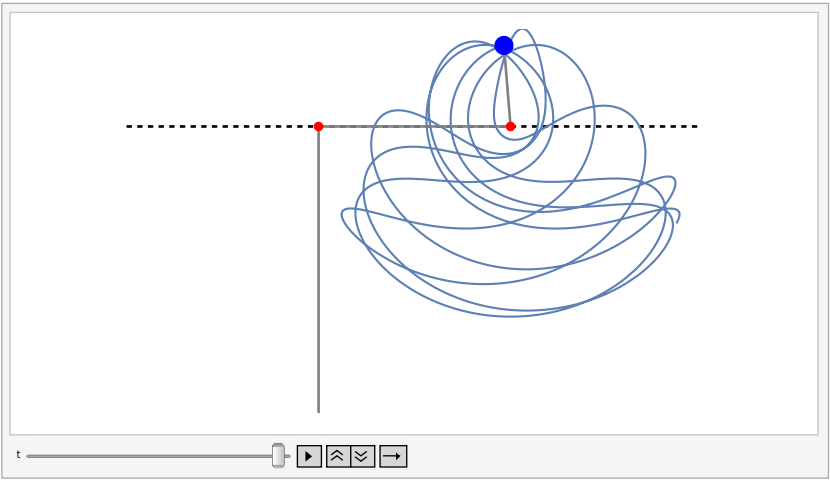
NDSolvemethod, allowing for result verification and the creation of cool animations like this one:
- B. Tuffilaro, A. Abbot, and J. Griffits. Atwood’s machine. American Journal of Physics, doi: 10.1119/1.13791, 1984. Link
- Л. Д. Ландау и Е. М Лифшиц. Теоретическая физика: Т.I Механика. Издательство Наука. 1988. --- 216 c.
- Нефедов Н.Н., Попов В.Ю., Волков В.Т. Обыкновенные дифференциальные уравнения. Курс лекций — М.: Физический факультет МГУ им. М.В. Ломоносова, 2016. — 200 с.