day1-basics

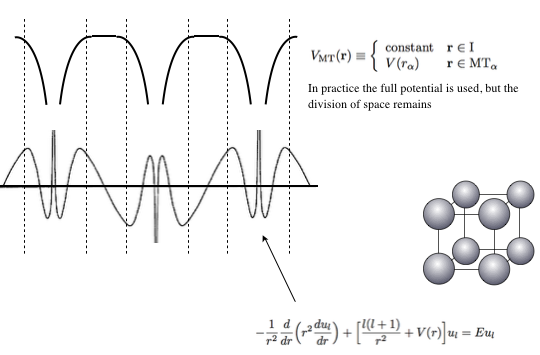
Introduction to RSPt and bcc Fe

Introduction

Manual

the manual of RSPt is stored in the documentation/manual/ folder in RSPt's repository. To obtain the manual in pdf format one needs to go to that directory and type:

latex manual.tex

three times.

RSPt's basis set

RSPt simulation files

To execute the rspt binary you need the following files:

data (compound specific info, what atoms, basic functions, etc...)
spts (information of the k-mesh)
atomdens (information of the overlapping atomic density, which is used as a starting guess)
symcof (Information about symmetries and basis)

An existing calculating also contains:

pot (the potential)
eparm (linearlization energies)

When setting up a calculation from scratch, one starts with one file called symt.inp. It contains the basic information such as lattice vectors, lattice parameter and atom positions. From this file many of the files needed to run a simulation is generated. Below follows a step-by-step description of how to setup a simulation of bcc Fe.

bcc Fe

0. Download tutorial from github

Download the tutorial from github by typing:

git clone https://github.com/RSPt-tutorials/day1-basics.git

This will download the following tutorial content:

This README.md file
symt.inp (RSPt input file for bcc Fe)
folder input (compare your input setup with this help folder)
folder lsda (compare your converged DFT calulations with this help folder)
folder lsda-dos (compare your DOS with the DOS in this help folder)
basis_set_visualization.png (figure schematically visualizing the basis functions in RSPt)

1. Preparations

Before using RSPt, make sure the same modules are loaded as when compiling RSPt. E.g. on Rackham, type:

module load intel/18.1 intelmpi/18.1

A convinient way is to load the module automatically at login by putting the command in the ~/.bashrc file.

2. Create simulation folder

To create a simulation from cratch one starts by creating and moving into a simulation folder, e.g.:

mkdir Fe
cd Fe

3. Create `symt.inp`

Create folder sym and move inside that folder:

mkdir sym
cd sym

The symt.inp should contain basic information about the system. For a complete overview of possible input parameters in symt.inp, check out documentation/manual. In our case a functioning symt.inp already exists which we can copy to our sym folder. The symt.inp works with free format, meaning keywords are used to categorize the information. The keywords in the provided symt.inp:

lengthscale (lattice parameters)
latticevectors (the latticevectors in column format)
spinpol (to tell RSPt that the simulation should be spin polarized)
mtradii (parameter to optimize Muffin-tin radius)
atoms (first number of atoms in the unitcell followed by (position, atomic number, coordinate keyword, identity-tag) of each atom. The coordinate keyword tells if the atomic position is expressed in lattice-vectors (using l) or in cartesian coordinates (using c). The identity-tag can be used to distinguish between otherwise equivalent atoms. This tag can also be used to generate spin-polarized atomic densities, by either using tag up or tag dn.)
lmax (how many spherical harmonics shall be used to express density and potential)

Once the symt.inp has the desired setup, type:

symt -all

Now many the folders atom, bin, bz, dta and some files should exist.

4. Generate atomic density

Starting from the main diretory:

cd atom
make

This will generate an atomic density which will be used as a starting point for the DFT calculations.

5. Generate k-mesh

Starting from the main diretory:

cd bz
cub

The user should now tell which symmetry-file to use when generating the k-mesh. Almost always, use the default option (read ../symcof) by pressing the enter key.

Then specify desired k-mesh, e.g. 12 12 12.

Input numerators for k-mesh shift vector, e.g. 0 0 0.

Input deminonators for k-mesh shift vector, e.g. 1 1 1.

Confirm the k-mesh by pressing the enter key.

Create tetrahedrons by pressing the enter key.

Finally type the enter key to quit the k-mesh generator.

One has to actually select which k-mesh rspt should use, in case many were created in the bz directory. To select the k-mesh generated by the commands above, type:

cd ..
link_spts 12_no

This generates symbolic links spts, tetra and kmap which point to the generated k-mesh in the bz directory.

6. `dta` folder settings

The dta folder contains many settings for the basis set. One has to copy two files:

cp dta/length_scale .
cp dta/strain_matrix .

There are two philosophies of how to edit the settings stored in the dta folder. Either one makes the wanted changes in the files in the dta folder or one leaves the dta folder unchanged and make the wanted changes at a later stage. In this tutorial we will do the latter.

7. Generate the `data` file

Generate the final input file, called data, by typing:

make data

Since we did no changes in the dta folder, we can instead make the wanted changes in the data file. (Note that it is the information in the data file which is being read by the rspt binary and not those in the dta folder.)

In this tutorial we want to use the LDA functional instead of the default PBE functional. We make this change by editing the data file. Instead of:

  lmax ntype  zval     . icorr     .  pmix   win   wmt f-rel sp-po     .
     8     1  16.0     8    34    1.  .500     t     t     f     t     1

Change the icorr value to 02, hence update to:

  lmax ntype  zval     . icorr     .  pmix   win   wmt f-rel sp-po     .
     8     1  16.0     8    02    1.  .500     t     t     f     t     1

The DFT mixing parameter pmix in the data file is .5 by default, which is usually too big. Let's change it to be .05 instead:

  lmax ntype  zval     . icorr     .  pmix   win   wmt f-rel sp-po     .
     8     1  16.0     8    02    1.  .050     t     t     f     t     1

There are differents methods for doing the integration in the reciprocal space. The default method uses tetrahedrons but we would like to change to a method which uses Fermi smearing. We achieve this by replacing the 1 on row 10 by a 0. We also change the temperature by editing the first value on row 13 to 0.0005. The rows 9-13 in the data file, about the k-integration, should now look like:

(i6)
     0
 (/ 2f12.0, i6)
       W(Ry)        dE/W     .
      0.0005          4.     0

We also want to modify the tail-energies so that all tail-energies are negative. (This gives more robust calculations it decreaces the condition number of the overlap matrix.) Change the first tail-energy from 0.3 to -0.1 on row 21 such that rows 20-23 look:

 (f12.0, f5.0, i1, i3, 3i2, l3, f6.0, i3, 6f12.0)
        -0.1   .01  0 1 0 1  f    .0  0          .0       
        -2.3   .01  0 1 0 1  f    .0  0          .0
        -1.5   .01  0 1 0 1  f    .0  0          .0

Finally the want to have a look at the linearization energies. The basis functions for Fe is described in the end of the data file:

    12 Bases
     0     1     1
     0     1     2
     0     1     3
     1     1     1
     1     1     2
     1     1     3
     2     1     1
     2     1     2
     0     2     1
     0     2     2
     1     2     1
     1     2     2
     4     4     3     4     5     6     7     8     9
     0     0     0     0     0     0     0     0     0
     4     4     3     4     5     6     7     8     9
     0     0     0     0     0     0     0     0     0
     3     3     3     4     5     6     7     8     9
     0     0     0     0     0     0     0     0     0
     3     3     3     4     5     6     7     8     9
     0     0     0     0     0     0     0     0     0

The first row (12 Bases) says that there are 12 l-projected basis functions. Then follows one row per basis function, where each row contains (l-quantum number, energy-set, tail-index). Thus, in the fist energy-set we have s, p and d basis funtions and in the second energy-set we only have s and p basis functions.

The last rows tells which principle quantum numbers and linearization flags the basis functions have. Since we do spin-polarized calculations there are four rows per energy-set (two rows for spin down and two for spin up). Let's focus on the first row:

     4     4     3     4     5     6     7     8     9

It says that the principle quantum numbers of the first energy-set, which we from above know has s, p and d functions, are: 4, 4, 3. Thus the basis functions of the first energy-set are: 4s, 4p and 3d.

The second energy-set has basis functions: 3s and 3p. Since the basis functions of the second energy set are lower in energy than the first energy-set it is common to change the linearlization flags of those basis functions to -1. We also change the linearlization flags in the first energy-set so that the 4s and 4p functions become orthogonal to 3s and 3p, respectively, by using 20 and 21. Finally we also change the linearization flag for the 3d functions to -1. Now, the information about the principle quantum numbers and the linearlization flags of the Fe basis functions should look like:

     4     4     3     4     5     6     7     8     9
    20    21    -1     0     0     0     0     0     0
     4     4     3     4     5     6     7     8     9
    20    21    -1     0     0     0     0     0     0
     3     3     3     4     5     6     7     8     9
    -1    -1     0     0     0     0     0     0     0
     3     3     3     4     5     6     7     8     9
    -1    -1     0     0     0     0     0     0     0

8. Execute the `rspt` binary

Now everything is ready and we want to execute the rspt binary. Either use an interactive session or submit a job.

To request an interactive session on the Rackham computer with 10 processors, type:

interactive -n 10 -t 00:15:00  --qos=short  -A g2018015

Once granted access, run RSPt by executing the rspt binary:

srun -n 10 rspt

This will run one DFT iteration and use 10 MPI ranks. To perform several iterations either use a bash-loop:

for ((i=1;i<=20;i++));do
  srun -n 10 rspt
done

or use the runs binary:

runs 'srun -n 10 rspt' 1e-8 20

The latter will run 20 DFT iterators or stop if the converge parameter fsq becomes smaller than 1e-8.

A submit jobscript should look something like:

#!/bin/bash -l
#SBATCH -A g2018015
#SBATCH -p core --qos=short
##SBATCH -p devel
#SBATCH -n 10
#SBATCH -t 00:15:00

echo "hello"
for ((i=1;i<=20;i++));do
  srun -n 10 rspt
done
echo "bye"

9. Analyze RSPt output

There are a few things to check to make sure the simulation is reliable:

The convergence parameter fsq is stored in the out file and as the first number in the convergence file. Its value should reach an acceptably small number before the simulation can be considered converged.
There should not be any star in the second column below the Energy parameters keyword.
The second number below the Fourier transform parameters keyword should be equal to 6.
The leakage value should be less than 0.1.
The muffin-tin value corresponding to the keyword 2S should be around 0.95.
The total energy is converged. To see how total energy and fsq have changed during the iterations type: grep 'e ' hist

10. Generate DOS

To generate density of states (DOS) and projected DOS (PDOS) for e.g. the 3d orbitals, one can provide a green.inp file. In our case its content can be:

matsubara
1024  60  60  10   ! nmats head body tail

convergency
1d-6 1d-5  0  0    ! ndelta sigma_acc maxiter maxsolveriter

energymesh
1001 -1.0 1.0 0.01

projection
1                  ! 1: MT, 2: ORT

spectrum
Dos Pdos

cluster
1 0              ! ntot udef [nsites]
1 2 1 1 0        ! t l e site basis[cubic harm] U J or F0 F2 F4 (F6)

Now just execute rspt once to obtain DOS and PDOS, stored in the following files:

dos.dat
pdos-0102010100-obs.dat To plot the Fe 3d PDOS in using gnuplot, type:

gnuplot

and then the gnuplot command:

p "pdos-0102010100-obs.dat" w l

To plot using Python, type:

ipython

and then the Python commands:

import matplotlib.pylab as plt 
import numpy as np
x = np.loadtxt("pdos-0102010100-obs.dat")
plt.plot(x[:,0],x[:,1])
plt.show()

dafer45/day1-basics