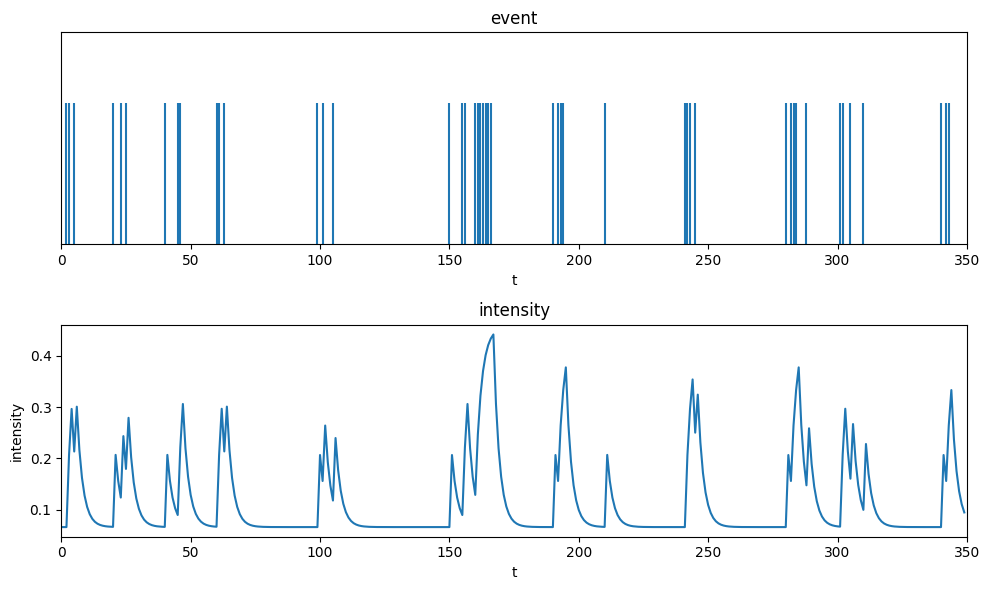
The probability density function of hawkes process for the observation period
$$ p_{[0,T]}(\boldsymbol{t}{n}) = \prod{i=1}^{n} \left[\mu + \sum_{j < i}g(t-t_j)\right] \times \exp\left[-\mu T - \sum_{i=1}^n\int_{t_i}^T g(s-t_i)ds \right] $$
where,
Assume the following for kernel functions
Maximum likelihood estimation of
The likelihood function
$$ \mathcal{L}(\boldsymbol{\theta}|\boldsymbol{t}n) = p{[0,T]}(\boldsymbol{t}_n | \boldsymbol{\theta}) $$
Estimate parameters by gradient descent method.
$$ \begin{aligned} \frac{\partial}{\partial\mu}\log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}n) &= \sum{i=1}^n \frac{1}{\lambda_i} - T \ \frac{\partial}{\partial a}\log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}n) &= \sum{i=1}^n \frac{1}{\lambda_i}\frac{\partial \lambda_i}{\partial a} - \sum_{i=1}^n [1 - \exp[-b(T-t_i)]] \ \frac{\partial}{\partial b}\log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}n) &= \sum{i=1}^n \frac{1}{\lambda_i}\frac{\partial \lambda_i}{\partial b} - \sum_{i=1}^n a(T-t_i) \exp[-b(T-t_i)] \end{aligned} $$ where, $$ \begin{aligned} \lambda_i &= \mu + \sum_{j<i}ab\exp[-b(t_i-t_j)] \ \frac{\partial \lambda_i}{\partial a} &= \sum_{j<i}b\exp[-b(t_i - t_j)] \ \frac{\partial \lambda_i}{\partial b} &= \sum_{j<i} a\exp[-b(t_i - t_j)][1-b(t_i-t_j)] \end{aligned} $$
Simple computation is
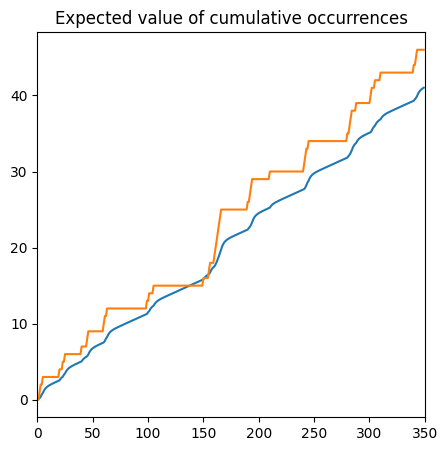
Introducing the above, we have the following asymptotic equation.
Using this, we can calculate
Start container
$ docker-compose up -d --build
Attach container
$ docker exec -it hawkes-process /bin/bash
Maximum likelihood estimation
$ python main.py