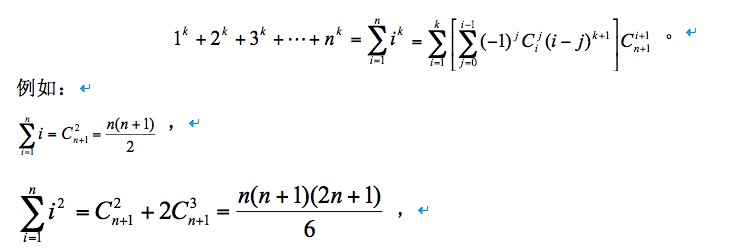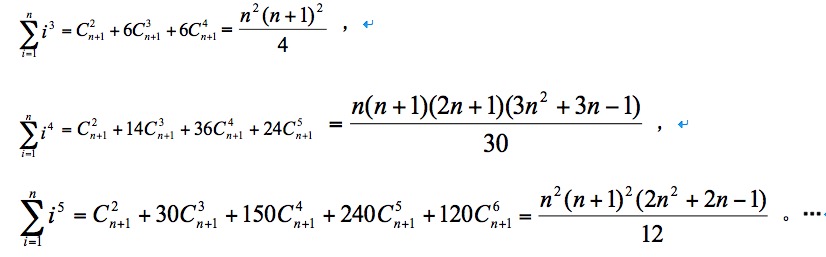acmer-qualification-code

1. printf

1.1 符号说明

      %a(%A)     浮点数、十六进制数字和p-(P-)记数法(C99)
      %c         字符
      %d         有符号十进制整数
      %f         浮点数(包括float和double)
      %e(%E)     浮点数指数输出[e-(E-)记数法]
      %g(%G)     浮点数不显无意义的零"0"
      %i         有符号十进制整数(与%d相同)
      %u         无符号十进制整数
      %o         八进制整数    e.g.     0123
      %x(%X)     十六进制整数0f(0F)   e.g.   0x1234
      %p         指针
      %s         字符串
      %%         "%"

1.2 对齐

      左对齐："-"   e.g.   "%-20s"
      右对齐："+"  e.g.   "%+20s"
      空格：若符号为正，则显示空格，负则显示"-"   e.g.   "%  6.2f"      
      #：对c,s,d,u类无影响；对o类，在输出时加前缀o；对x类，在输出时加前缀0x；对e,g,f 类当结果有小数时才给出小数点

1.3 格式化输出

 ［标志］［输出最少宽度］［．精度］［长度］类型
  "％-md" ：左对齐，若m比实际少时，按实际输出。
  "%m.ns"：输出m位，取字符串(左起)n位，左补空格，当n>m or m省略时m=n.
  						e.g. "%7.2s"	输入CHINA
                                       输出"     CH"
  "%m.nf"：输出浮点数，m为宽度，n为小数点右边数位
           				e.g. "%3.1f"   输入3852.99
                                        输出3853.0

2. 符号的英文读法

+  plus 加号；正号
-  minus 减号；负号
± plus or minus 正负号
× is multiplied by 乘号
÷ is divided by 除号
＝ is equal to 等于号
≠ is not equal to 不等于号
≡ is equivalent to 全等于号
≌ is equal to or approximately equal to 等于或约等于号
≈ is approximately equal to 约等于号
＜  is less than 小于号
＞ is greater than 大于号
≮ is not less than 不小于号
≯  is not more than 不大于号
≤ is less than or equal to 小于或等于号
≥ is more than or equal to 大于或等于号
%  per cent 百分之…
‰ per mill 千分之…
∞  infinity 无限大号
∝ varies as 与…成比例
√ (square) root 平方根
∵ since; because 因为
∴ hence 所以
∷ equals, as (proportion) 等于，成比例
∠ angle  角
⌒ semicircle 半圆
⊙ circle 圆
○ circumference 圆周
π pi 圆周率
△  triangle 三角形
⊥ perpendicular to 垂直于
∪ union of 并，合集
∩  intersection of 交，通集
∫ the integral of …的积分
∑ (sigma) summation of 总和
° degree 度
′ minute 分
″ second 秒
℃ Celsius system 摄氏度
{  open brace, open curly 左花括号
} close brace, close curly 右花括号
(  open parenthesis, open paren 左圆括号
) close parenthesis, close paren 右圆括号
() brakets/ parentheses 括号
[ open bracket 左方括号
]  close bracket 右方括号
[] square brackets 方括号
. period, dot 句号，点
|  vertical bar, vertical virgule 竖线
& ampersand, and, reference, ref 和，引用
* asterisk, multiply, star, pointer 星号，乘号，星，指针
/ slash, divide, oblique 斜线，斜杠，除号
// slash-slash, comment 双斜线，注释符
# pound 井 号
 backslash, sometimes escape 反斜线转义符，有时表示转义符或续行符
~ tilde 波浪符
.  full stop 句号
, comma 逗号
: colon 冒号
; semicolon 分号
?  question mark 问号
! exclamation mark (英式英语) exclamation point (美式英语)
‘  apostrophe 撇号
- hyphen 连字号
– dash 破折号
… dots/ ellipsis 省略号
”  single quotation marks 单引号
“” double quotation marks 双引号
‖ parallel 双线号
& ampersand = and
～ swung dash 代字号
§ section; division 分节号
→ arrow 箭号；参见号

3. C/C++头文件

///C
#include <assert.h>         //设定插入点
#include <ctype.h>          //字符处理
#include <errno.h>          //定义错误码
#include <float.h>          //浮点数处理
#include <limits.h>         //定义各种数据类型最值常量
#include <locale.h>         //定义本地化函数
#include <math.h>           //定义数学函数
#include <setjmp.h>         //非局部跳转
#include <signal.h>         //信号处理
#include <stdarg.h>         //变长变元表
#include <stddef.h>
#include <stdio.h>          //定义输入／输出函数
#include <stdlib.h>         //定义杂项函数及内存分配函数
#include <string.h>         //字符串处理
#include <time.h>           //定义关于时间的函数


///////////////////////////////////////////////////////////////////////////////
///标准 C++
///C语言部分略
#include <algorithm>        //STL 通用算法
#include <bitset>           //STL 位集容器
#include <complex>          //复数类
#include <deque>            //STL 双端队列容器
#include <exception>        //异常处理类
#include <fstream>          //文件输入/输出
#include <functional>       //STL 定义运算函数（代替运算符）
#include <limits>
#include <list>             //STL 线性列表容器
#include <map>              //STL 映射容器
#include <iomanip>
#include <ios>              //基本输入／输出支持
#include <iosfwd>           //输入／输出系统使用的前置声明
#include <iostream>
#include <istream>          //基本输入流
#include <ostream>          //基本输出流
#include <queue>            //STL 队列容器
#include <set>              //STL 集合容器
#include <sstream>          //基于字符串的流
#include <stack>            //STL 堆栈容器    
#include <stdexcept>        //标准异常类
#include <streambuf>        //底层输入／输出支持
#include <string>           //字符串类
#include <utility>          //STL 通用模板类
#include <vector>           //STL 动态数组容器
#include <cwchar>
#include <cwctype>
using namespace std;

///////////////////////////////////////////////////////////////////////
///C99 增加
#include <complex.h>        //复数处理
#include <fenv.h>           //浮点环境
#include <inttypes.h>       //整数格式转换
#include <stdbool.h>        //布尔环境
#include <stdint.h>         //整型环境
#include <tgmath.h>         //通用类型数学宏
///////////////////////////////////////////////////////////////////////

4. 注意事项

变量名count会和<algorithm>中的count冲突
cin和scanf不能同时使用，cout和printf不能同时使用
GCC/G++中，输出double应该使用printf("%f") 而不是lf
如果用scanf接收了一行数据，再用gets, gets会直接接收到空串！因为，scanf接受了一行数据以后换行符仍然在缓冲区中，gets()遇到换行符，接收会结束. 解决方法，scanf 后加一个getchar()
精度问题
2^31-1 =0x7fffffff
-2^31 =-0x7fffffff-1
精确的pi :double pi=acos(-1);

5. N次方求和

6. 字符串处理

/**
 *颠倒一个字符串的顺序 "abc\0" – "cba\0"
 *array	为需要颠倒顺序的字符串
 *length 为字符串array的长度
 */
int stringReverse(char *array,int length){
    int i = 0,j = length - 1;
    while(i < j){
        char cha = array[i];
        array[i] = array[j];
        array[j] = cha;i++;j--;
    }
    return 1;
}

7. 进制转换

/**
 *将任意进制数转换成整型范围内的十进制数
 *str   为base进制数
 *base  为str的进制
 *length为str的长度
 */
int myPow(int a,int b){
    int rs = 1;
    while(b--){rs *= a;}
    return rs;
}
int anyToDecimal(char *str,int base,int length){
	int decimal = 0,i;
	for(i = 0;i < length;i++){
		if(str[i] >= 65)/*为十六进制的时候*/{
			decimal += myPow(base,length-1 - i)*(str[i] - 'A' + 10);
		}
		else if(str[i] <= '9'){
			decimal += myPow(base,length-1 - i)*(str[i] - '0');
		}
	}
	return decimal;
}

8. 栈

/**
 *栈 C++
 *clear() push() top() empty() pop() size()
 *free()
 */
typedef int T;
struct myStack{
    int curr,size_limit;
    T *array;
    myStack(int s){//必须传入栈的大小
        curr = -1; size_limit = s;
        array = new T[s];
    }
    void clear(){curr = -1;}/*清空栈 重新使用*/
    void free(){delete array;clear();}/*释放栈 不能再使用*/
    T top(){
        if(curr > -1){return array[curr];}
        else return curr;}
    bool push(T v){
        if(curr+1 < size_limit){array[++curr] = v;return true;}
        return false;}
    bool empty(){
        if(curr < 0)return true;
        else return false;}
    void pop(){curr--;}
    int  size(){return curr+1;}
};

8. 表达式转换

/**
*自己定义操作符的优先级
*/
int priorityLevle(const char x){
}
/**
*自己定义操作符的结合性，左或者右
*/
int rightAssociative(const char x){
    switch(x){
        case '^':{ return 1;}
    }
    return 0;
}	
/**
*shunting_yard: infix expression to RPN
*中缀转换成后缀
*传入中缀表达式expression，RPN保存在result中
*/
void shunting_yard(char *result,const char *expression){
    stack<char> my;
    int len = strlen(expression), r = 0;
    for(int  i = 0;i < len;i++){
        if(expression[i] == ' ') continue;
        if(expression[i] >= '0' && expression[i] <= '9'){
            //是数字直接加到输出队列
            result[r++] = expression[i];
        }
        else{//操作符或者括号
            ///以下代码需要根据具体情况修改
            ///需要注意操作符的优先级和结合性
            if(r != 0 && result[r-1] != ' ') result[r++] = ' ';//数字之间必须要用空格隔开
            if(expression[i] == ')'){
                while(!my.empty() && my.top() != '('){
                    //遇到右括号的时候 要将括号里边的表达式看成一个整体
                    //将左括号之后的内容都弹出
                    result[r++] = my.top(); my.pop();
                }
                if(!my.empty()) my.pop();//弹出左括号
            }
            else{
                while(expression[i] != '('//左括号直接入栈
                    &&!my.empty()//栈为空的时候也直接入栈
                    ///如果是操作符 需要弹出栈里优先级比它高 或者 优先级相等但是是左结合的操作符
                    && my.top() != '('//遇到左括号相当于栈为空
                    && (
                        (priorityLevle(my.top()) > priorityLevle(expression[i]))
                  ||(priorityLevle(my.top())==priorityLevle(expression[i])&& !rightAssociative(my.top()))
                       )
                    ){
                    result[r++] = my.top(); my.pop();
                }
                my.push(expression[i]);//将这个操作符入栈
            }
        }
    }
    while(!my.empty()){
        result[r++] = my.top(); my.pop();
    }
    result[r] = '\0';
}

9. 搜索

/**
 *二分查找
 *如果找到flag为1 posi为所查找到的位置
 *如果没找到flag为0 posi为该值应该插入的位置
 *传入的区间为[left,right)
 */

struct node{
    int flag;//0表示不存在
    int posi;//返回插入或者删除的位置
};
struct node *binarySearch(int *array,int value,int left,int right){
    struct node *pointer = (struct node*)malloc(sizeof(struct node));
    pointer->flag = 0;pointer->posi = -1;
    if(right == 0){//left == -1 impossible
        pointer->flag = pointer->posi = 0;
        return pointer;
    }
    while(left <= right){
        int mid = ((left + right) >> 1);
        if(value == array[mid]){
            pointer->flag = 1;
            pointer->posi = mid;
            return pointer;
        }
        else{
			(value > array[mid])?(left=mid+1):(right=mid-1);
		}
	}
	pointer->posi = left;return pointer;
}

10. 排序

/**
 *二叉排序树模板
 *插入函数 插入之前应先申请一个要插入的pointer节点 然后传进去
 *查找函数 root为根节点 parent等于root value为要查找的值 flag为0返回查找到的节点的
 *父节点这样便于删除时使用  flag 为1返回查找到的节点的指针
 *删除函数 传入要删除的节点的父节点和要删除的节点 如果待删节点为父节点的左孩子flag=0
 *如果为右孩子 flag = 1
 *构造函数 将一个数组从start到end（不包括end）的范围构造为一个二叉排序树 root为根节
 *点
 */
struct node{
    int value;
    struct node *left,*right;
};	
int insertBST(struct node *root,struct node *pointer){
    if(root == NULL){
        root = pointer;//插入的节点的左右孩子的初始值一定要为NULL
    }
    else if(pointer->value < root->value){
        insertBST(root->left ,pointer);
    }
    else{
        insertBST(root->right,pointer);
    }
    return 1;
}
struct node *searchBST(struct node *root,struct node *parent,int value,int flag){
    if(root == NULL){
        return NULL;
    }
    else if(root->value == value){
        //返回的是要查找节点的父节点或者是要查找的节点
        //使用父节点是因为这样便于删除的时候使用父节点进行删除
        if(flag == 0){return parent;}
        else{return root;}
    }
    else if(value < root->value){
        return searchBST(root->left,root,value,flag);
    }
    else{
        return searchBST(root->right,root,value,flag);
    }
    return NULL;
}
int deleteBST(struct node *parent,struct node *pointer,int flag){
    if(pointer->left == NULL && pointer->right == NULL){
        if(flag == 0){
            //pointer 为parent的左子叶
            parent->left  = NULL;
        }
        else{
            //pointer 为parent的右子叶
            parent->right = NULL;
        }
        free(pointer);
    }
    else if(pointer->left == NULL){
        if(flag == 0){
            parent->left  = pointer->right;
        }
        else{
            parent->right = pointer->right;
        }
        free(pointer);
        //如果struct node中用一个数组保存left和right
        //就可以写成 parent->array[flag] = pointer->right;

    }
    else if(pointer->right == NULL){
        if(flag == 0){
            parent->left  = pointer->left;
        }
        else{
            parent->right = pointer->left;
        }
        free(pointer);
    }
    else{
        parent         = pointer;
        struct node *s = pointer->right;
        //找右子树中最左的节点 或者找左子树中最右的节点
        //然后和要删除的位置交换value
        //这里选择前者
        while(s->left != NULL){
            parent = s;
            s      = s->left;
        }
        pointer->value = s->value;
        parent->left   = s->right;
        //因为s肯定没有左子树 所以把右子树接在父节点的左指针上就行了
        free(s);
    }
    return 1;
}
int constructBST(struct node *root,int *array,int start,int end){
    struct node *pointer = (struct node*)malloc(sizeof(struct node));
    while(start < end){
        pointer->value = array[start];
        pointer->left  = NULL;
        pointer->right = NULL;
        insertBST(root,pointer);
        start++;
    }
    return 1;
}

/**
 *quickSort ,快速排序，传入要排序的数组和需要排序的范围[left,right]
 *从小到大
 */
void quickSort(int left,int right,int array[]){
    int i = left,j = right,x = array[(left+right)/2];
    do{
        while(array[i] < x)i++;
        while(array[j] > x)j--;//使左边的值都比右边的小
        if(i <= j) {std::swap(array[i++],array[j--]);}
    }while(i < j);//i >= j
    if(i < right)quickSort(i,right,array);
    if(j > left)quickSort(left,j,array);
}

/**
 *heapSort 堆排序模板 （大根堆）
 */
int mySwap(int *a,int *b){
if(a == b) return;
	(*a) = (*a) ^ (*b);
	(*b) = (*a) ^ (*b);
	(*a) = (*a) ^ (*b);
    return 1;
}	
int sift(int array[],int k,int m)//one-based
{
//把k到m范围内的值调整为大根堆
    int i = k,j = i<<1;//置i为要筛的节点 j 为i的左孩子
    while(j <= m){//仍然在范围之内
        if(j < m && array[j] < array[j+1]){//右孩子存在 且左孩子小于右孩子
            j++;//因为要建大根堆 所以选择孩子中较大者进行交换
        }
        if(array[i] > array[j]){
            break;//不需要再向下比较 因为之前也是调整过的大根堆
        }
        else{
            mySwap(&array[i],&array[j]);
            i = j;j = (i<<1);//被筛节点移动到j节点 计算左孩子
        }
    }
    return 1;
}
int heapSort(int array[],int n){// one-based 从1开始保存的 到n结束 left_child = 2*parent
    int i;
    for(i = n>>1;i >= 1;i--){
        sift(array,i,n);//初始建堆 从 最后一个非终端节点到 1
    }
    for(i  = 1;i < n;i++){//重复执行移走堆顶并重建堆的操作
        mySwap(&array[1],&array[n-i+1]);//从n到2 不断和堆顶交换 one-based
        sift(array,1,n - i);//重建堆
    }
    return 1;
}

11. 递归

/**
 *汉诺塔 递归实现
 */
int move(int n,char x,char y){
    printf("move %d from %c to %c\n",n,x,y);//输出移动过程
    return 1;
}
int hanoi(int n,char a,char b,char c){//将n个盘子借助b从a移动到c
    if(n==1){move(1,a,c);}
    else{
        hanoi(n-1,a,c,b);//把n-1个盘子借助c从a移动到b
        move(n,a,c);//把第n个盘子从a移动到c
        hanoi(n-1,b,a,c);//将n-1个盘子借助a从b移动到c
    }
    return 1;
}

12. 链表

/**
 *构建一个未赋值的循环单链表 至少有头和尾两个节点
 */
struct node{
    int 	value;
    struct node *next;
};
struct node *constructRecurrentSingleChain(int start,int end){
    struct node *head = (struct node*)malloc(sizeof(struct node));
    struct node *tail = (struct node*)malloc(sizeof(struct node));

    head->next = tail;
    tail->next = head;
    //head->value= -1;
    //tail->value= -1;
    while(start != end){
        struct node *new_node = (struct node*)malloc(sizeof(struct node));
        //new_node->value     = start;根据具体情况进行赋值
        new_node->next        = head;
        tail->next            = new_node;
        tail                  = new_node;
        start++;
    }
    return head;
}

/**
 *构建未赋值的循环双链表 至少有头和尾两个节点
 */
struct node{
    int value;
    struct node *prev;
    struct node *next;
};
struct node *constructRecurrentDoubleChain(int start,int end){
    struct node *head = (struct node*)malloc(sizeof(struct node));
    struct node *tail = (struct node*)malloc(sizeof(struct node));

    head->prev = tail;
    head->next = tail;
    tail->next = head;
    tail->prev = head;
    //head->value= -1;
    //tail->value= -1;
    while(start != end){
        struct node *new_node = (struct node*)malloc(sizeof(struct node));
        //new_node->value       = start;
        tail->next            = new_node;
        head->prev            = new_node;
        new_node->prev        = tail;
        new_node->next        = head;
        tail                  = new_node;
        start++;
    }
    return head;
}

13. 大数

/**
 *大数的加法 乘法运算
 *效率很低 不能用于算大数阶乘
 */
 class BigInteger
 {
public:
     BigInteger();
     BigInteger(int);
     BigInteger(string);
     bool Display();
     friend BigInteger operator +(const BigInteger&,const BigInteger&);
     friend BigInteger operator *(const BigInteger&,const BigInteger&);
     friend ostream&   operator<<(std::ostream&,BigInteger&);
private:
     static const int max_len = 100000;
 public:
     int len;
     int array[max_len];
 };
 BigInteger::BigInteger(){
     memset(array,0,sizeof(array));
     //或者将sizeof(array) 换成 max_len*4
     len = 0;
 }
 BigInteger::BigInteger(string digit){
     memset(array,0,sizeof(array));
     len = digit.size();
     for(int i = 0;i < len;i++){
         array[i] = digit[len - i - 1] - '0';
     }
 }
 BigInteger::BigInteger(int digit){
     memset(array,0,sizeof(array));
     if(digit == 0)len = 1;
     else		len = 0;
     while(digit != 0){
         array[len++] = digit % 10;
         digit        = digit / 10;
     }
 }
 bool BigInteger::Display(){
     for(int i = len - 1;i >= 0;i--) cout << array[i];
     return true;
 }
 std::ostream& operator<<(ostream &out,BigInteger &digit){
     digit.Display(); return out;
 }
 BigInteger operator +(const BigInteger &augend,const BigInteger &addend){
     BigInteger result;
     result.len = max(augend.len,addend.len);
     for(int i = 0;i < result.len;i++)
         result.array[i] = augend.array[i] + addend.array[i];
     for(int i= 0;i < result.len;i++){
         if(result.array[i] >= 10){
             result.array[i] -= 10;
             result.array[i+1]++;
         }
     }
     if(result.array[result.len] > 0){result.len++;}
     return result;
 }
 BigInteger operator *(const BigInteger &multiplicand,const BigInteger &multiplier)
 {
     BigInteger result;
     result.len = multiplicand.len + multiplier.len - 1;
     for(int i = 0;i < multiplicand.len;i++){
         for(int j = 0;j < multiplier.len;j++)
             result.array[i + j] += multiplicand.array[i]*multiplier.array[j];
     }
     for(int i = 0;i < result.len;i++){
         if(result.array[i] > 9){
             result.array[i+1] += result.array[i] / 10;
             result.array[i]   %= 10;
         }
     }
     if(result.array[result.len] > 0) result.len++;
     while(result.len > 1 && result.array[result.len-1] == 0)
         result.len--;//为0的时候不用去掉第一位的0
     return result;
 }

/**
 *n的阶乘 结果为大数，保存在array数组中
 *end - 1 到 0为结果 (end-1)在前,为高位
 */
int factorial(int *array,int n){
    int end = 1; array[0] = 1;
    for(int i = 2;i <= n;i++){
        int r = 0;
        for(int j = 0;j < end;j++){
            //乘以每一位
            int t = array[j]*i+r;
            array[j] = t%10;
            r = t/10;
        }
        while(r){
            array[end++] = r % 10;
            r /= 10;
        }
    }
    return end;
}

/**
 *大数模板(浙大)
 *注意这里的int可能会超 void div(bignum_t a,const int b,int& c)
 */
#define DIGIT 	3//千进制
#define DEPTH	1000//千进制
#define MAX     1000//位数
typedef int bignum_t[MAX+1];

int read(bignum_t a,istream& is=cin){
	char buf[MAX*DIGIT+1],ch;
	int i,j;
	memset((void*)a,0,sizeof(bignum_t));
	if (!(is>>buf))	return 0;
	for (a[0]=strlen(buf),i=a[0]/2-1;i>=0;i--)
		ch=buf[i],buf[i]=buf[a[0]-1-i],buf[a[0]-1-i]=ch;
	for (a[0]=(a[0]+DIGIT-1)/DIGIT,j=strlen(buf);j<a[0]*DIGIT;buf[j++]='0');
	for (i=1;i<=a[0];i++)
		for (a[i]=0,j=0;j<DIGIT;j++)
			a[i]=a[i]*10+buf[i*DIGIT-1-j]-'0';
	for (;!a[a[0]]&&a[0]>1;a[0]--);
	return 1;
}

void write(const bignum_t a,ostream& os=cout){
	int i,j;
	for (os<<a[i=a[0]],i--;i;i--)
		for (j=DEPTH/10;j;j/=10)
			os<<a[i]/j%10;
}

int comp(const bignum_t a,const bignum_t b){
	int i;
	if (a[0]!=b[0])
		return a[0]-b[0];
	for (i=a[0];i;i--)
		if (a[i]!=b[i])
			return a[i]-b[i];
	return 0;
}

int comp(const bignum_t a,const int b){
	int c[12]={1};
	for (c[1]=b;c[c[0]]>=DEPTH;c[c[0]+1]=c[c[0]]/DEPTH,c[c[0]]%=DEPTH,c[0]++);
	return comp(a,c);
}

int comp(const bignum_t a,const int c,const int d,const bignum_t b){
	int i,t=0,O=-DEPTH*2;
	if (b[0]-a[0]<d&&c)
		return 1;
	for (i=b[0];i>d;i--){
		t=t*DEPTH+a[i-d]*c-b[i];
		if (t>0) return 1;
		if (t<O) return 0;
	}
	for (i=d;i;i--){
		t=t*DEPTH-b[i];
		if (t>0) return 1;
		if (t<O) return 0;
	}
	return t>0;
}

void add(bignum_t a,const bignum_t b){
	int i;
	for (i=1;i<=b[0];i++)
		if ((a[i]+=b[i])>=DEPTH)
			a[i]-=DEPTH,a[i+1]++;
	if (b[0]>=a[0])
		a[0]=b[0];
	else
		for (;a[i]>=DEPTH&&i<a[0];a[i]-=DEPTH,i++,a[i]++);
	a[0]+=(a[a[0]+1]>0);
}

void add(bignum_t a,const int b){
	int i=1;
	for (a[1]+=b;a[i]>=DEPTH&&i<a[0];a[i+1]+=a[i]/DEPTH,a[i]%=DEPTH,i++);
	for (;a[a[0]]>=DEPTH;a[a[0]+1]=a[a[0]]/DEPTH,a[a[0]]%=DEPTH,a[0]++);
}

void sub(bignum_t a,const bignum_t b){
	int i;
	for (i=1;i<=b[0];i++)
		if ((a[i]-=b[i])<0)
			a[i+1]--,a[i]+=DEPTH;
	for (;a[i]<0;a[i]+=DEPTH,i++,a[i]--);
	for (;!a[a[0]]&&a[0]>1;a[0]--);
}

void sub(bignum_t a,const int b){
	int i=1;
	for (a[1]-=b;a[i]<0;a[i+1]+=(a[i]-DEPTH+1)/DEPTH,a[i]-=(a[i]-DEPTH+1)/DEPTH*DEPTH,i++);
	for (;!a[a[0]]&&a[0]>1;a[0]--);
}

void sub(bignum_t a,const bignum_t b,const int c,const int d){
	int i,O=b[0]+d;
	for (i=1+d;i<=O;i++)
		if ((a[i]-=b[i-d]*c)<0)
			a[i+1]+=(a[i]-DEPTH+1)/DEPTH,a[i]-=(a[i]-DEPTH+1)/DEPTH*DEPTH;
	for (;a[i]<0;a[i+1]+=(a[i]-DEPTH+1)/DEPTH,a[i]-=(a[i]-DEPTH+1)/DEPTH*DEPTH,i++);
	for (;!a[a[0]]&&a[0]>1;a[0]--);
}

void mul(bignum_t c,const bignum_t a,const bignum_t b){
	int i,j;
	memset((void*)c,0,sizeof(bignum_t));
	for (c[0]=a[0]+b[0]-1,i=1;i<=a[0];i++)
		for (j=1;j<=b[0];j++)
			if ((c[i+j-1]+=a[i]*b[j])>=DEPTH)
				c[i+j]+=c[i+j-1]/DEPTH,c[i+j-1]%=DEPTH;
	for (c[0]+=(c[c[0]+1]>0);!c[c[0]]&&c[0]>1;c[0]--);
}

void mul(bignum_t a,const int b){
	int i;
	for (a[1]*=b,i=2;i<=a[0];i++){
		a[i]*=b;
		if (a[i-1]>=DEPTH)
			a[i]+=a[i-1]/DEPTH,a[i-1]%=DEPTH;
	}
	for (;a[a[0]]>=DEPTH;a[a[0]+1]=a[a[0]]/DEPTH,a[a[0]]%=DEPTH,a[0]++);
	for (;!a[a[0]]&&a[0]>1;a[0]--);
}

void mul(bignum_t b,const bignum_t a,const int c,const int d){
	int i;
	memset((void*)b,0,sizeof(bignum_t));
	for (b[0]=a[0]+d,i=d+1;i<=b[0];i++)
		if ((b[i]+=a[i-d]*c)>=DEPTH)
			b[i+1]+=b[i]/DEPTH,b[i]%=DEPTH;
	for (;b[b[0]+1];b[0]++,b[b[0]+1]=b[b[0]]/DEPTH,b[b[0]]%=DEPTH);
	for (;!b[b[0]]&&b[0]>1;b[0]--);
}

void div(bignum_t c,bignum_t a,const bignum_t b){
	int h,l,m,i;
	memset((void*)c,0,sizeof(bignum_t));
	c[0]=(b[0]<a[0]+1)?(a[0]-b[0]+2):1;
	for (i=c[0];i;sub(a,b,c[i]=m,i-1),i--)
		for (h=DEPTH-1,l=0,m=(h+l+1)>>1;h>l;m=(h+l+1)>>1)
			if (comp(b,m,i-1,a)) h=m-1;
			else l=m;
	for (;!c[c[0]]&&c[0]>1;c[0]--);
	c[0]=c[0]>1?c[0]:1;
}

void div(bignum_t a,const int b,long long & c){
	int i;
	for (c=0,i=a[0];i;c=c*DEPTH+a[i],a[i]=c/b,c%=b,i--);
	for (;!a[a[0]]&&a[0]>1;a[0]--);
}

void sqrt(bignum_t b,bignum_t a){
	int h,l,m,i;
	memset((void*)b,0,sizeof(bignum_t));
	for (i=b[0]=(a[0]+1)>>1;i;sub(a,b,m,i-1),b[i]+=m,i--)
		for (h=DEPTH-1,l=0,b[i]=m=(h+l+1)>>1;h>l;b[i]=m=(h+l+1)>>1)
			if (comp(b,m,i-1,a)) h=m-1;
			else l=m;
	for (;!b[b[0]]&&b[0]>1;b[0]--);
	for (i=1;i<=b[0];b[i++]>>=1);
}

int length(const bignum_t a){
	int t,ret;
	for (ret=(a[0]-1)*DIGIT,t=a[a[0]];t;t/=10,ret++);
	return ret>0?ret:1;
}

int digit(const bignum_t a,const int b){
	int i,ret;
	for (ret=a[(b-1)/DIGIT+1],i=(b-1)%DIGIT;i;ret/=10,i--);
	return ret%10;
}

int zeronum(const bignum_t a){
	int ret,t;
	for (ret=0;!a[ret+1];ret++);
	for (t=a[ret+1],ret*=DIGIT;!(t%10);t/=10,ret++);
	return ret;
}

void comp(int* a,const int l,const int h,const int d){
	int i,j,t;
	for (i=l;i<=h;i++)
		for (t=i,j=2;t>1;j++)
			while (!(t%j))
				a[j]+=d,t/=j;
}

void convert(int* a,const int h,bignum_t b){
	int i,j,t=1;
	memset(b,0,sizeof(bignum_t));
	for (b[0]=b[1]=1,i=2;i<=h;i++)
		if (a[i])
			for (j=a[i];j;t*=i,j--)
				if (t*i>DEPTH)
					mul(b,t),t=1;
	mul(b,t);
}

void combination(bignum_t a,int m,int n){
	int* t=new int[m+1];
	memset((void*)t,0,sizeof(int)*(m+1));
	comp(t,n+1,m,1);
	comp(t,2,m-n,-1);
	convert(t,m,a);
	delete []t;
}

void permutation(bignum_t a,int m,int n){
	int i,t=1;
	memset(a,0,sizeof(bignum_t));
	a[0]=a[1]=1;
	for (i=m-n+1;i<=m;t*=i++)
		if (t*i>DEPTH)
			mul(a,t),t=1;
	mul(a,t);
}

14. 并查集

int father[15];
void makeSet(){
    for(inti = 0;i <= n;i++){
        father[i] = i;
    }
}
int findSet(int x){
    if(x != father[x]){
        father[x] = findSet(father[x]);
    }
    returnfather[x];
}
void unionSet(int x,int y){
    x = findSet(x);
    y = findSet(y);
    father[x] = y;
}

15. 状态压缩

/**
 *状态压缩法求阶乘，虽然可以求但这只是状态压缩恰好的一个性质 它主要用在动态规划中
 *注释里的是f[13] = f[12] + f[5] + f[9] 的工作过程，t -= t & -t 就是将最开始的t的每位1取出来，取      
 *出来的那位1和原来的值t异或就把那位1变成0了，有点别扭 :( 
 */	
long long f[1<<20] = {};
f[0] = 1;//f[2^0 - 1] = f[0] = 1 (0的阶乘为1)
for(int i = 1;i < (1<<n);i++){// 1 到 2^n - 1
    for(int t = i; t > 0; t -= (t & -t)){
        //f(01101) = f(00101) + f(01001) + f(01100)
        //1 t = 13
        //2 13 -= 1
        //3 12 -= 4
        //4 8  -= 8
        f[i] += f[i ^ (t & -t)];//将某些位变为0 计算和
        //1 f[(01101) ^ (01101 & 10011)] = f[01100]
        //2 f[(01101) ^ (01100 & 10100)] = f[01001]
        //3 f[(01101) ^ (01000 & 11000)] = f[00101]
    }
}
// n! = f[(1<<n)-1]

16. 树状数组

/**
 *一维树状数组,树状数组C[],输入的数组A[]
 *A[] C[]都是从1开始的 在build之前C[]初始化为0
 */

int lowbit(int x){
    return x & (x^(x-1));//这一步是把x的二进制表示中的最低位1取出来
    //x   = ***100
    //x-1 = ***011
    //x ^ (x-1) = 000111
    //x & (x ^ (x-1)) = 000100

    //return x&(-x);//另一种写法
    //x  = ***100
    //-x = ---011 + 1 = ---100;
    //x&-x = 000100;
}
void add(int i,int v,int upper){//对A[i]进行加v操作 同时更新C
    //对A[i]的更新直接不要放在这里 因为build也要调用该函数
    while(i <= upper){
        C[i] += v; i += lowbit(i);
    }
}
void build(int begin,int end){//根据A[begin]到A[end]构建树状数组
    while(begin <= end){
        add(begin,A[begin],end);
    }
}
int sum(int i){//求前n项和
    int sum = 0;
    while(i >= 1){
        sum += C[i]; i -= lowbit(i);
    }
    return sum;
}

/**
 *二维树状数组
 *二维树状数组和一维几乎一样
 */

int lowbit(int x){
    return x & (x^(x-1));
}
void add(int i,int j,int v,int upper){//增加
    int t_i,t_j;
    for(t_i = i;t_i <= upper;t_i += lowbit(t_i)){
        for(t_j = j;t_j <= upper;t_j += lowbit(t_j)){
            C[t_i][t_j] += v;
        }
    }
}
int query(int i,int j){//查询
    int sum = 0,t_i,t_j;
    for(t_i = i;t_i > 0;t_i -= lowbit(t_i)){
        for(t_j = j;t_j > 0;t_j -= lowbit(t_j)){
            sum += C[t_i][t_j];
        }
    }
    return sum;
}

17. 线段树

/**
 *树状数组是前序和，应用范围要窄，线段树可以求区间和、区间最大值等等
 *下面是求线段树求区间和的示例，可以根据具体情况修改
 */
#define MAX 100000
struct node{
    int left,right;
    long long sum,weight;
}tree[MAX];
int A[MAX];//MAX_n
void build(int i,int a,int b){//构建线段树 i为层数 初始为1 ，传入区间[a,b]
    //tree[i].left tree[i].right为节点i的左右边界
    if(a != b){
        tree[i].left = a;tree[i].right= b;
        build(i<<1,a,(a+b)>>1);//递归构造左子树
        build((i<<1)+1,((a+b)>>1)+1,b);//递归构造右子树
        tree[i].sum  = tree[i<<1].sum + tree[(i<<1)+1].sum;//回溯 左右子树的和等于父节点
    }
    else{
        tree[i].left = tree[i].right = a;
        tree[i].sum  = A[a];//A[]为输入的数组
        return;
    }
    tree[i].weight = 0;
}
int add(int i,int a,int b,int v){//将某个区间的所有值加上v
    if(tree[i].left == a && tree[i].right == b){
        //恰好是这个区间
        tree[i].weight += v;//将这个值保存而不是直接累加
	   //查询的时候再进行更新 节省时间开销
        return 1;
    }
    else{
        //不是该区间但是属于该区间
        tree[i].sum += v*(b - a + 1);
    }
    int mid = (tree[i].left+tree[i].right) >> 1;
    if(a <= mid && b > mid){
        add(i<<1,a,mid,v);
        add((i<<1)+1,mid+1,b,v);
    }
    else{
        add((i<<1)+(b<=mid?0:1),a,b,v);
    }
    return 1;
}
long long query(int i,int a,int b){//查询某个区间的所有值的和
    int mid = (tree[i].left+tree[i].right) >> 1;
    if(tree[i].left == a && tree[i].right == b){
        return tree[i].sum + (tree[i].right - tree[i].left + 1)*tree[i].weight;
    }
    else if(tree[i].weight != 0){
        tree[i].sum            += (tree[i].right - tree[i].left + 1)*tree[i].weight;//首先更新自己
        tree[i<<1].weight      += tree[i].weight;//然后传递给左右子树
        tree[(i<<1)+1].weight  += tree[i].weight;
        tree[i].weight = 0;//自身清零
    }
    if(a <= mid && b > mid){
        return query(i<<1,a,mid) + query((i<<1)+1,mid+1,b);
    }
    return query((i<<1) + (b<=mid?0:1),a,b);
}

/**
 *二维线段树
 *调用add,query,build时注意传参时的大小顺序，左小于右
 *二维线段树的x维度和y维度表示的意义不一定是一样的
 *下面是求平面上的矩形面积和(去掉重复区域后的面积和)，可以根据具体情况修改
 */
#define MAX 1500
vector<double> x;
vector<double> y;//用于离散化
struct y_node{
    int left,right;
    double len;//被覆盖的区间长度
};	
struct x_node{
    int left,right;
    double area;//被覆盖的面积
    struct y_node sub[MAX];
}tree[MAX];

void buildSub(int i,int j,int yl,int yr){
    tree[i].sub[j].left  = yl;
    tree[i].sub[j].right = yr;
    tree[i].sub[j].len = 0;
    if(yr - yl == 1){
        return;
    }
    buildSub(i,j<<1,yl,(yl+yr)>>1);
    buildSub(i,(j<<1)+1,((yl+yr)>>1),yr);//最小元是个线段所以不加1
}
void build(int i,int xl,int xr,int ylm,int yrm){
    tree[i].left = xl;tree[i].right= xr;tree[i].area = 0;
    if(xr - xl == 1){
        buildSub(i,1,ylm,yrm);//建立子树 只对叶子节点建立子树
        return;
    }
    build(i<<1,xl,(xl+xr)>>1,ylm,yrm);
    build((i<<1)+1,((xl+xr)>>1),xr,ylm,yrm);
}
void addSub(int i,int j,int yl,int yr){
    if(tree[i].sub[j].left == yl && tree[i].sub[j].right == yr){
        tree[i].sub[j].len = y[tree[i].sub[j].right] - y[tree[i].sub[j].left];
        return;
    }
    int mid = (tree[i].sub[j].left + tree[i].sub[j].right)>>1;
    if(yl < mid && yr > mid){
        addSub(i,(j<<1),yl,mid);
        addSub(i,(j<<1)+1,mid,yr);
    }
    else{
        addSub(i,(j<<1)+((yl >= mid)?1:0),yl,yr);
    }
    tree[i].sub[j].len = mymax(tree[i].sub[j].len,tree[i].sub[(j<<1)].len + tree[i].sub[(j<<1)+1].len);
}
void add(int i,int xl,int xr,int yl,int yr){//

    if(tree[i].right - tree[i].left == 1){//元区间
        addSub(i,1,yl,yr);//对y坐标加边 并计算长度
        tree[i].area = tree[i].sub[1].len*(x[xr]-x[xl]);//计算面积
        return;
    }
    int mid = (tree[i].left + tree[i].right)>>1;
    if(xl < mid && xr > mid){
        add((i<<1),xl,mid,yl,yr);
        add((i<<1)+1,mid,xr,yl,yr);
    }
    else{
        add((i<<1)+((xl >= mid)?1:0),xl,xr,yl,yr);
    }
    //更新面积
    tree[i].area = tree[(i<<1)].area + tree[(i<<1)+1].area;
}
double querySub(int i,int j,int ya,int yb){
    if(tree[i].sub[j].left == ya && tree[i].sub[j].right == yb){
        return tree[i].sub[j].len;
    }
    else{
        //不是目标区间但包含目标区间
        //do something
    }
    int mid = (ya+yb)>>1;
    if(ya <= mid && yb > mid){
        return querySub(i,j<<1,ya,mid) + querySub(i,(j<<1)+1,mid,yb);
    }
    else return querySub(i,(j<<1)+(yb<=mid?0:1),ya,yb);
}
double query(int i,int xa,int xb,int ya,int yb){
    if(tree[i].left == xa && tree[i].right == xb){
        return tree[i].area;
    }
    else{
        //do something
    }
    int mid = (xa+xb)>>1;
    if(xa <= mid && xb > mid){
        return query(i<<1,xa,mid,ya,yb) + query((i<<1)+1,mid,xb,ya,yb);
    }
    else return query((i<<1)+(xb<=mid?0:1),xa,xb,ya,yb);
}
//main中的离散化代码
sort(x.begin(),x.end());
sort(y.begin(),y.end());//排序之后去重
x.resize(unique(x.begin(),x.end()) - x.begin());
y.resize(unique(y.begin(),y.end()) - y.begin());

18. Trie树

/**
 *trie树，hash的方式，用空间换时间 注意别忘了创建根节点
 */
#define MAX 256 //每个节点可能有多少个孩子
struct node{
    ///数据域
    int used;//标记是否有对应的字母
    struct node *next[MAX];
};
void create(struct node *t){
    for(int i = 0;i < MAX;i++){
        t->next[i] = new struct node;
        ///initialize
    }
}	
void trieInsert(struct node *curr,const char *str,const int len){
    for(int i = 0;i < len;i++){
        //在当前节点的孩子中找
        int index = (int)str[i];
        if(curr->next[index]->used == 0){//没有这个字母
            curr->next[index]->used = 1;
            create(curr->next[index]);//创建它的孩子
        }
        curr = curr->next[index];
    }
    ///do something
}

19. 矩阵

/**
 *矩阵快速幂(2行2列)
 */
typedef double dataType;
struct matrix{
    dataType mat[2][2];
    matrix(){memset(mat,0,sizeof(mat));}//初始化为0
    matrix(double v1,double v2,double v3,double v4){mat[0][0] = v1;mat[0][1] = v2;mat[1][0] = v3;mat[1][1]=v4;}
    matrix operator*(const matrix &b){
        matrix rs;
        for(int i = 0;i < 2;i++){
            for(int k = 0;k < 2;k++){
                for(int j = 0;j < 2;j++){
                    rs.mat[i][j] += mat[i][k]*b.mat[k][j];
                }
            }
        }
        return rs;
    }
};	
matrix fastPower(matrix a,int po){
    //a^po
    matrix rs(1,0,0,1);//初始化为1
    while(po){
        if(po&1){rs = rs*a;}
        a = a*a;po = (po>>1);
    }
    return rs;
}

20. 精度处理

/**
 *返回0表示x==0，-1表示x < 0, 1表示x大于0
 *complf(a-b) == 0, a == b 或者 fabs(a-b) < eps
 *complf(a-b) != 0, a != b 或者 fabs(a-b) > eps
 *complf(a-b) <  0, a <  b 或者 a - b < -eps
 *complf(a-b) >  0, a >  b 或者 a - b > eps
 *complf(a-b) <= 0, a <= b 或者 a - b < eps
 *complf(a-b) >= 0, a >= b 或者 a - b > -eps
 */	
#define eps 1e-8
int complf(double x){ return x < -eps?-1:((x < eps)?0:1);}

21. 动态规划

/**
 *0-1 背包 （二维实现，可以优化到一维）
 *注释中所说的对象可以为一个物体，也可以为一种方案，视题目而定
 */

dp[n+1][v+1];
memset(dp[0],0,sizeof(int)*(v+1));//不放任何对象时，不管背包容量多少的价值都是0
for(i = 1;i <= n;i++){//从第一个对象开始
    //处理第i 个对象，在当前背包容量为j的时候选还是不选这个对象
    for(j = 0;j <= v;j++){//枚举每个容量
        if(volume[i] > j){//这个对象肯定是不能放在容量为j的背包里的
            //如果j < volume[i]，相减之后就小于0了
            dp[i][j] = dp[i-1][j];
        }
        else{//如果体积刚好等于剩余的容量也不一定会被放进去
             //因为可能有其它几个对象组合之后的价值比这个单个对象的高
            dp[i][j] = mymax(dp[i-1][j],dp[i-1][j-volume[i]]+weight[i]);
        }
    }
}//结果保存在 dp[n][v]中，即对前n个对象做出取舍后的最优解

22. 素数生成

/**
 *筛法求素数 筛法求素数，找到[1,MAXL]的所有素数
 */
#define MAXL 100000
#define MAXC 50000
bool not_prime[MAXL+1];//用于判断是否被筛掉 2的倍数都会被筛掉，但是没有标记
int primeTable[MAXC];//保存素数
long long getPrime(){
    long long i,j,step,prime_num = 1;
    not_prime[0] = not_prime[1] = true;
    primeTable[0] = 2;//第一个素数是2
    for(i = 3;i <= MAXL;i+=2){
        if(not_prime[i] == false){
            primeTable[prime_num++] = i;
            for(j = i*i,step = 2*i;j <= MAXL;j += step){not_prime[j] = true;}
        }
    }
    return prime_num;
}

23. 素数测试

/**
 *Miller-Rabin 素数测试
 *随机选取s个基 出错的概率至多为 1/(2^s)，50已经足够了
 *RAND_MAX包含在stdlib中，不同的库会有不同，但都至少为32767
 */

/**
 *快速幂取模 返回 a^n mod m
 */
long long exp_mod(long long a,long long n,long long m){
    //x*y mod m = ((x%m) * (y%m))%m
    if(n == 1)
        return a % m;
    else if(n == 0)
        return 1;
    if(n&1){//奇数 a^n = (a^(n-1))*a
        return ((a%m)*exp_mod(a,n-1,m)) % m;
    }
    else{//偶数 a^n = (a^(n>>1))^2
        long long t = exp_mod(a,n>>1,m) % m;
        return t*t%m;
    }
}

int witness(int a,int n){
    //a^(n-1) = 1 (mod n)
    int t = 0,u = n-1;
    while(!(u&1)){t++; u = (u>>1);}// n - 1 = u*(2^t)
    long long x[2]; x[0] = x[1] = exp_mod(a,u,n);
    for(int i = 1;i <= t;i++){
        x[1] = x[0]*x[0]%n;
        if(x[1] == 1 && x[0] != 1 && x[0] != (n-1)){
            return 1;//检测到一个非平凡平方根
        }
        x[0] = x[1];
    }
    if(x[1] != 1) return 1;
    return 0;
}
int millerRabin(int n,int s = 50){
    if(n == 2) return 1;
    else if(!(n&1)) return 0;
    for(int i = 0;i < s;i++){
        int a = (int)((rand()*1.0/RAND_MAX)*(n-2)) + 1;
        if(witness(a,n)){
            //a^(n-1) = 1 (mod n) 如果n为素数，那么对于a(1<=a<=n-1)都满足这个等式
            return 0;//基数a是n为合数的证据
        }
    }
    return 1;//几乎可以确定n是个素数
}

24. 最大公约数/最小公倍数

/**
 *最大公约数 gcd
 *最小公倍数 lcm = a*b/gcd(a,b)
 */
int gcd(int a,int b){
	return b ? gcd( b,a % b ) : a;
}	
int lcm(int a,int b){
	return a/gcd(a,b)*b;
}

/**
 *二进制欧几里得辗转相除法求gcd
 *传参的时候注意a >= b
 */
typedef long long int64;
int64 binaryGcd(int64 a,int64 b){
    if(a == b) return a;
    if((a&1) && (b&1)){
        return binaryGcd(a-b,b);
    }	
    else if((a&1) == 0 && (b&1) == 0){
        return 2*binaryGcd(a>>1,b>>1);
    }
    else if((a&1)){
        return binaryGcd(a,b>>1);
    }
    return binaryGcd(mymax(a>>1,b),mymin(a>>1,b));
}

25. 欧拉 phi 函数

/**
 *欧拉phi函数  返回小于x且与x互质的数的个数
 */
int euler_phi(int x){
    int a = ceill(sqrt(x)),i,rs = x;
    for(i = 2;i <= a;i++){
        if(x % i == 0){
            rs -= rs/i;//减去 在这rs个元素中有i因子的 数 的个数
            while(x % i == 0){x /= i;}//将x中含有i因子的数去掉
            if(x == 1)break;//x已经到1了
        }
    }
    if(x != 1) {rs -= (rs / x);}
    return rs;
}

26. 快速幂取模

/**
 *快速幂取模 返回 a^n mod m
 */
int exp_mod(int a,int n,int m){
    //x*y mod m = ((x%m) * (y%m))%m
    if(n == 1)
        return a % m;
    else if(n == 0)
        return 1 % m;
    if(n&1){//奇数 a^n = (a^(n-1))*a
        return ((a%m)*exp_mod(a,n-1,m)) % m;
    }
    else{//偶数 a^n = (a^(n>>1))^2
        long long t = exp_mod(a,n>>1,m) % m;
        return t*t%m;
    }
}

27. 扩展欧几里得

/**
 *扩展欧几里德 ax+by = gcd(a,b) 解出x,y
 */
long long extendedEuclid(long long a,long long b,long long &x,long long &y){
    if(b == 0){
        x = 1; y = 0; return a;
    }
    else{
        long long gcd,x1,y1;
        gcd = extendedEuclid(b,a%b,x1,y1);
        x = y1; y = x1 - (a/b)*y1;
        return gcd;
    }
}

28. 梅森素数

/**
 *扩展欧几里德 ax+by = gcd(a,b) 解出x,y
 */
long long extendedEuclid(long long a,long long b,long long &x,long long &y){
    if(b == 0){
        x = 1; y = 0; return a;
    }
    else{
        long long gcd,x1,y1;
        gcd = extenedEuclid(b,a%b,x1,y1);
        x = y1; y = x1 - (a/b)*y1;
        return gcd;
    }
}

29. 最大流

/**
 *最大流 传入源点 汇点和顶点数
 *graph[u][v]为u到v的剩余流量 （residual flow）
 *初始的流量根据具体情况而定，如果没有边相连流量为0
 *graph[v][u]为流过e(u,v)的流量
 */
#define INF 1000000000
#define MAX 100
int Edmonds_Karp(int source, int sink, int vertex_num){
    int maxFlow = 0;
    while(true) {
        int head, tail, pre_of[MAX], my_queue[MAX];
        head = tail = 0;//初始化队列
        my_queue[tail++] = source;//放入源点
        memset(pre_of, -1, sizeof(pre_of));////(pre_of[v],v) 代表边(u,v)
        while(head < tail){
            int u = my_queue[head++];
            for(int v = 1; v <= vertex_num; v ++) {//也可以从0开始
                if(pre_of[v] == -1 && graph[u][v] > 0){
                    my_queue[tail++] = v;/*入队*/
                    pre_of[v] = u;/*保存这条边*/
                    if(u == sink)   break;
                }
            }
            if(pre_of[sink] != -1) break; //找到增广路径
        }
        if(pre_of[sink] == -1) break;//没有增广路径
        int min_flow = INF;
        for(int v = sink; v != source; v = pre_of[v]) {
            min_flow = mymin(min_flow, graph[pre_of[v]][v]);
            //对pre保存的路径进行回溯找到最小的流(最大可流通流量)
        }
        maxFlow += min_flow;
        for(int v = sink; v != source; v = pre_of[v]) {//更新流网络
            graph[pre_of[v]][v] -= min_flow;
            graph[v][pre_of[v]] += min_flow;
        }
    }
    return maxFlow;
}

/**
 *ISAP求最大流
 */
typedef  struct {
	int v, next, val;
} edge;
const int MAXN = 20010;
const int MAXM = 500010;

edge e[MAXM];
int p[MAXN], eid;

inline void init() {
	memset(p, -1, sizeof(p));
	eid = 0;
}

//有向
inline void insert1(int from, int to, int val) {
	e[eid].v = to;
	e[eid].val = val;
	e[eid].next = p[from];
	p[from] = eid++;

	swap(from, to);

	e[eid].v = to;
	e[eid].val = 0;
	e[eid].next = p[from];
	p[from] = eid++;
}

//无向
inline void insert2(int from, int to, int val) {
	e[eid].v = to;
	e[eid].val = val;
	e[eid].next = p[from];
	p[from] = eid++;

	swap(from, to);

	e[eid].v = to;
	e[eid].val = val;
	e[eid].next = p[from];
	p[from] = eid++;
}

int n, m; //n为点数 m为边数
int h[MAXN];
int gap[MAXN];

int source, sink;
inline int dfs(int pos, int cost) {
	if (pos == sink) {
		return cost;
	}
	int j, minh = n - 1, lv = cost, d;

	for (j = p[pos]; j != -1; j = e[j].next) {
		int v = e[j].v, val = e[j].val;

		if(val > 0) {
			if (h[v] + 1 == h[pos]) {
				if (lv < e[j].val) {
					d = lv;
				} else {
					d = e[j].val;
				}

				d = dfs(v, d);
				e[j].val -= d;
				e[j ^ 1].val += d;
				lv -= d;

				if (h[source] >= n) {
					return cost - lv;
				}

				if (lv == 0) {
					break;
				}
			}

			if (h[v] < minh)	{
				minh = h[v];
			}
		}
	}

	if (lv == cost) {
		--gap[h[pos]];

		if (gap[h[pos]] == 0) {
			h[source] = n;
		}

		h[pos] = minh + 1;
		++gap[h[pos]];
	}

	return cost - lv;
}

int sap(int st, int ed) {
	source = st;
	sink = ed;
	int ret = 0;
	memset(gap, 0, sizeof(gap));
	memset(h, 0, sizeof(h));

	//gap[st] = n;
	gap[0] = n;
	while (h[st] < n) {
		ret += dfs(st, INT_MAX);
	}
	return ret;
}

30. 最短路

/**
 *SPFA可以用来求单源最短路径和求解差分约束
 *可以处理负边和负权回路
 */	
#define INF 1000000000
#define MAX 50010//最大的点数，根据题目
struct node{int u,v,weight,next;}edge[10*MAX];//边数一般比点数多
int head[MAX];int count = 0;
void add(int u,int v,int c){//邻接表的加边操作
    edge[count].u = u;edge[count].v = v;edge[count].weight = c;
    edge[count].next = head[u];head[u] = count++;
}
int SPFA(int  ll,int rr){
//根据具体情况对i点到起点的长度进行初始化
    int d[MAX];for(int i = ll;i <= rr;i++){d[i] = -INF;}d[ll] = 0;
    queue<int> my_queue;my_queue.push(ll);//放入起点
    bool in_queue[MAX] = {};//用于判断某点当前是否在队列中
    while(!my_queue.empty()){
        int start = my_queue.front();my_queue.pop();
        in_queue[start] = false;//拿出来了 所以不在队列中了
        for(int  i = head[start]; i != -1; i = edge[i].next){
            int u = edge[i].u,v = edge[i].v,weight_of_uv = edge[i].weight;
            if(d[v] < d[u] + weight_of_uv){
                d[v] = d[u] + weight_of_uv;
                if(!in_queue[v]){
                    //可以入队且不在队列中
                    //可能会继续松弛表示可以入队
                    my_queue.push(v);
                    in_queue[v] = true;//标记为在队列中
                }
            }
        }
    }
    return d[rr];//根据具体情况返回一个结果
}

/**
 *dijkstra求最短路，用优先队列优化
 *传入源点和顶点个数(注意顶点是从0还是1开始)
 *如果只计算源点到单个目的点的最短路，需将flag标记为1 并传入目的点
 *注意head,countt等初始化
 */
#define MAX 1100
#define INF 1000000000
struct node{
    int u,v,w,next;//顶点结构体
}edge[100100];
int head[MAX],countt=0;//每次都要初始化
void add(int u,int v,int w){//加边
    edge[countt].u = u;
    edge[countt].v = v;
    edge[countt].w = w;
    edge[countt].next = head[u];head[u] = countt++;
}
struct node2{
    int ver,dist; //顶点和dist[ver]
    node2(int v,int d){ver = v;dist = d;}
};	
bool operator > (const node2 &a,const node2 &b){
    //重载优先队列的 > 运算符
    if(a.dist > b.dist)return true;
    return false;
}
bool operator < (const node2 &a,const node2 &b){
    //重载优先队列的 < 运算符
    if(a.dist < b.dist)return true;
    return false;
}
int dijkstra(int source,int vertex_num,int end=-1,int flag=0){
    int dist[MAX];
    //优先队列(小根,top为最小值)
    priority_queue<node2,vector<node2>,greater<node2> > my;
    for(int i = 1;i <= vertex_num;i++){
        dist[i] = INF;
    }dist[source] = 0;
    my.push(node2(source,0));//放入源点
    int pre_of[MAX]; memset(pre_of,-1,sizeof(pre_of));
    while(!my.empty()){
        node2 u = my.top();my.pop();
        if(flag && u.ver == end){return dist[u.ver];}
        if(dist[u.ver] == INF) break;//肯定没有更小的
        for(int i = head[u.ver];i != -1;i = edge[i].next){
            int v = edge[i].v,w = edge[i].w;
            if(dist[v] > dist[u.ver] + w){
                dist[v] = dist[u.ver] + w;
                pre_of[v] = u.ver;//保存路径
                my.push(node2(v,dist[v]));
            }
        }
    }
    ///dist[i]保存的是源点到所有i点的最短距离
    return 1;
}

31. 最小生成树

/**
 *kruskal求最小生成树
 */
#define MAX 1000
struct node{int u,v,cost;}array[MAX*MAX];
int edge_count;//边的数量
int father[MAX];
void makeSet(int n){
    for(int i = 1;i <= n;i++){
        //根据具体条件对并查集初始化
        father[i] = i;
    }
}
int find(int x){
    if(father[x] != x){
        return father[x] = find(father[x]);
    }
    return father[x];
}
void unionSet(int x,int y){
    //将x所在的集合合并到y所在的集合
    father[find(x)] = find(y);
}
int kruskal(){
    int total_cost = 0;//总花费
    //对边排序
    pseudocode: sort(array,array+edge_count);
    for(int i = 0;i < edge_count;i++){
        if(find(array[i].u)==find(array[i].v)){
            //端点在同一个集合的不能添加进去
            //因为会构成回路
            continue;
        }
        total_cost += array[i].cost;
        unionSet(array[i].u,array[i].v);
    }
    return total_cost;
}

31. 有向图的强连通分量

/**
 *Tarjan algorithm for strongly connected component
 *求强连通分量的tarjan算法,邻接表表示
 *注意数组的初始化
 */
int dfs_order[MAX], lowest[MAX];
int my_stack[MAX],visited[MAX],in_stack[MAX];
int mark_num,top;
struct node{
    int u,v,next;
}edge[MAX*5];
void tarjan_scc(int u){
    dfs_order[u] = lowest[u] = mark_num++;
    my_stack[top++] = u;visited[u] = 1;in_stack[u] = 1;
    for(int i = head[u];i != -1;i = edge[i].next){
        int v = edge[i].v;
        if(!visited[v]){
            tarjan_scc(v);
            lowest[u] = mymin(lowest[u],lowest[v]);
        }
        else if(in_stack[v]){
            lowest[u] = mymin(lowest[u],dfs_order[v]);
        }
    }
    if(dfs_order[u] == lowest[u]){
        int p;
        do{
            p = my_stack[--top];in_stack[p] = 0;
            ///这里出栈的是当前的一个强连通分量
            ///根据具体情况处理
        }while(u != p);
    }
}

32. 无向图的双连通分量

/**
 *Tarjan algorithm for strongly connected component
 *求强连通分量的tarjan算法,邻接表表示
 *注意数组的初始化
 */
int dfs_order[MAX], lowest[MAX];
int my_stack[MAX],visited[MAX],in_stack[MAX];
int mark_num,top;
struct node{
    int u,v,next;
}edge[MAX*5];
void tarjan_scc(int u){
    dfs_order[u] = lowest[u] = mark_num++;
    my_stack[top++] = u;visited[u] = 1;in_stack[u] = 1;
    for(int i = head[u];i != -1;i = edge[i].next){
        int v = edge[i].v;
        if(!visited[v]){
            tarjan_scc(v);
            lowest[u] = mymin(lowest[u],lowest[v]);
        }
        else if(in_stack[v]){
            lowest[u] = mymin(lowest[u],dfs_order[v]);
        }
    }
    if(dfs_order[u] == lowest[u]){
        int p;
        do{
            p = my_stack[--top];in_stack[p] = 0;
            ///这里出栈的是当前的一个强连通分量
            ///根据具体情况处理
        }while(u != p);
    }
}

33. 二分图的最大匹配

/**
 *二分图的最大匹配（邻接矩阵），交大模板
 *graph初始化为0，返回最大匹配数
 *注意要给nx ny赋值
 */
#define MAX 510
int nx,ny,graph[MAX][MAX],sy[MAX],cx[MAX],cy[MAX];
int path(int u){
    for(int v = 1; v <= ny;v++){
        if(graph[u][v] && !sy[v]){
            sy[v] = 1;
            if(!cy[v] || path(cy[v])){
                cx[u] = v; cy[v] = u;
                return 1;
            }
        }
    }
    return 0;
}
int maximumMatch(){
    int i,ret = 0;
    memset(cx,0,sizeof(cx));
    memset(cy,0,sizeof(cy));
    for(i = 1;i <= nx;i++){
        if(!cx[i]){//
            memset(sy,0,sizeof(sy));
            ret += path(i);
        }
    }
    return ret;
}

34. 叉积/点与线段/线段与线段

struct point{double x,y;};
struct segment{point a,b;};
/**
 *cross product
 *(p2-p1) X (q2-q1) -> aXb
 *(p2.x-p1.x,p2.y-p1.y) X (q2.x-q1.x,q2.y - q1.y)
 *结果大于0说明 b到a为顺时针 等于0说明a b共线 小于0说明b到a为逆时针
 */
double crossProduct(const point &p1, const point &p2,const point &q1,const point &q2){
    return (p2.x-p1.x)*(q2.y-q1.y) - (p2.y-p1.y)*(q2.x-q1.x);
}


/**
 *判断点p是否在线段（q1,q2）上
 *判断点p是否在线段s上
 */
int onSegment(const point &p, const point &q1, const point &q2){
    double rs = crossProduct(q1,p,q2,p);
    if(complf(rs) == 0){
        //共线
        if(p.x <= mymax(q1.x,q2.x) && p.x >= mymin(q1.x,q2.x)
        && p.y <= mymax(q1.y,q2.y) && p.y >= mymin(q1.y,q2.y)){
            return 1;
        }
    }
    return 0;
}
int onSegment(const point &p,const segment &s){
    double rs  = crossProduct(s.a,p,s.b,p);
    if(rs >= 0 && rs < eps){
        if(p.x <= mymax(s.a.x,s.b.x) && p.x >= mymin(s.a.x,s.b.x)
        && p.y <= mymax(s.a.y,s.b.y) && p.y >= mymin(s.a.y,s.b.y)){
            return 1;
        }
    }
    return 0;
}


/**
 *判断两线段是否相交
 */
int intersect(const segment &s1, const segment &s2){
    //先判断一条线段的端点是否在另外一条线段上
    if(onSegment(s1.a,s2)
    || onSegment(s1.b,s2)
    || onSegment(s2.a,s1)
    || onSegment(s2.b,s1)){
        //
        return 1;
    }
    //再判断线段的两个端点是否在另外一条线段的两侧
    if(crossProduct(s1.a,s1.b,s1.a,s2.a)*crossProduct(s1.a,s1.b,s1.a,s2.b) < 0
    && crossProduct(s2.a,s2.b,s2.a,s1.a)*crossProduct(s2.a,s2.b,s2.a,s1.b) < 0){
        return 1;
    }
    return 0;

35. 组合

/**
 *组合 从a个数中选b个的选法C(a,b)
 */
long long combination( long long a,long long b )
{
    long long i,sum = 1;
    if( a-b < b ) b = a-b;
    for( i = 0; i < b; i++ ){
        sum *= ( a - i ); sum/=i+1;
    }
    return sum;
}

36. Catalan Number

/**
 *网上找的模板 验证过前一百的catalan数
 */
#include<iostream>
#include<string>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<algorithm>
using namespace std;

#define MAXN 9999
#define DLEN 4

class BigNum{
private:
   int a[300];//DLEN digs for a position
   int len;
public:
   BigNum(){len = 1;memset(a,0,sizeof(a));}
   BigNum(const int b);
   BigNum(const BigNum & T);

   bool     Bigger(const BigNum &) const;
   BigNum & operator=(const BigNum &);
   BigNum & Add(const BigNum &);
   BigNum & Sub(const BigNum &);
   BigNum operator+(const BigNum &) const;
   BigNum operator-(const BigNum &) const;
   BigNum operator*(const BigNum &) const;
   BigNum operator/(const int   &) const;
   void Print();
};
BigNum::BigNum(const int b)
{
   int c,d = b; len = 0;
   memset(a,0,sizeof(a));
   while(d > MAXN){
      c = d - d / (MAXN + 1) * (MAXN + 1);
      d = d / (MAXN + 1);
      a[len++] = c;
   }a[len++] = d;

}
BigNum::BigNum(const BigNum & T) : len(T.len)
{
   int i; memset(a,0,sizeof(a));
   for(i = 0 ; i < len ; i++) a[i] = T.a[i];
}
bool  BigNum::Bigger(const BigNum & T) const
{
   int ln;
   if(len > T.len) return true;
   else if(len == T.len){
      ln = len - 1;
      while(a[ln] == T.a[ln] && ln >= 0) ln--;
      if(ln >= 0 && a[ln] > T.a[ln]) return true;
      else return false;
   }
   else return false;
}
BigNum & BigNum::operator=(const BigNum & n)
{
   len = n.len; memset(a,0,sizeof(a));
   for(int i = 0 ; i < len ; i++)
      a[i] = n.a[i];
   return *this;
}
BigNum & BigNum::Add(const BigNum & T)
{
   int i,big;
   big = T.len > len ? T.len : len;
   for(i = 0 ; i < big ; i++){

      a[i] = a[i] + T.a[i];
      if(a[i] > MAXN){
         a[i + 1]++;
         a[i] = a[i] - MAXN - 1;
      }
   }
   if(a[big] != 0) len = big + 1;
   else len = big;
   return *this;
}
BigNum & BigNum::Sub(const BigNum & T)
{
   int i,j,big;
   big = T.len > len ? T.len : len;
   for(i = 0 ; i < big ; i++){
      if(a[i] < T.a[i]){
         j = i + 1;
         while(a[j] == 0) j++;
         a[j--]--;
         while(j > i) a[j--] += MAXN;
         a[i] = a[i] + MAXN + 1 - T.a[i];
      }
      else a[i] -= T.a[i];
   }
   len = big;
   while(a[len - 1] == 0 && len > 1) len--;
   return *this;
}
BigNum BigNum::operator+(const BigNum & n) const
{
   BigNum a = *this; a.Add(n);

   return a;
}
BigNum BigNum::operator-(const BigNum & T) const
{
   BigNum b = *this;b.Sub(T);
   return b;
}
BigNum BigNum::operator*(const BigNum & T) const
{
   BigNum ret;
   int i,j,up;
   int temp,temp1;

   for(i = 0 ; i < len ; i++){
      up = 0;
      for(j = 0 ; j < T.len ; j++){
         temp = a[i] * T.a[j] + ret.a[i + j] + up;
         if(temp > MAXN){
            temp1 = temp - temp / (MAXN + 1) * (MAXN + 1);
            up = temp / (MAXN + 1);
            ret.a[i + j] = temp1;
         }
         else {
            up = 0;
            ret.a[i + j] = temp;
         }
      }
      if(up != 0)
         ret.a[i + j] = up;
   }
   ret.len = i + j;
   while(ret.a[ret.len - 1] == 0 && ret.len > 1) ret.len--;
   return ret;
}
BigNum BigNum::operator/(const int & b) const
{
   BigNum ret;
   int i,down = 0;

   for(i = len - 1 ; i >= 0 ; i--){
      ret.a[i] = (a[i] + down * (MAXN + 1)) / b;
      down = a[i] + down * (MAXN + 1) - ret.a[i] * b;
   }
   ret.len = len;
   while(ret.a[ret.len - 1] == 0) ret.len--;
   return ret;
}
void BigNum::Print()
{
   int i;
   cout << a[len - 1];
   for(i = len - 2 ; i >= 0 ; i--){
      cout.width(DLEN);
      cout.fill('0');
      cout << a[i];
   }cout << endl;
   //输出的时候注意这里的换行,注意C++的输出不能和C和输出混用

}

int main(){
     int i;
     BigNum s[101]; s[1]=1;
     for(i=1;i<100;i++){
      s[i+1]=BigNum(4*i+2)*(s[i])/(i+2);
     }
     while(scanf("%d",&i) && i != -1){
         s[i].Print();
     }
    return 0;
}

37. 通项公式

//F[n]=a*F[n-1]+b*F[n-2]的通项公式的求解
//此类方程的特征方程为 x^2 - a^x - b*1 = 0;
//假设方程的解为q1,q2 ; F[n]=c1 * q1^n + c2 * q2^n
//将f[0] ,f[1]等已知的结果代入，就可求得c1,c2

daishanxiang/acmer-qualification-code

acmer-qualification-code

1. printf

1.1 符号说明

1.2 对齐

1.3 格式化输出

2. 符号的英文读法

3. C/C++头文件

4. 注意事项

5. N次方求和

6. 字符串处理

7. 进制转换

8. 栈

8. 表达式转换

9. 搜索

10. 排序

11. 递归

12. 链表

13. 大数

14. 并查集

15. 状态压缩

16. 树状数组

17. 线段树

18. Trie树

19. 矩阵

20. 精度处理

21. 动态规划

22. 素数生成

23. 素数测试

24. 最大公约数/最小公倍数

25. 欧拉 phi 函数

26. 快速幂取模

27. 扩展欧几里得

28. 梅森素数

29. 最大流

30. 最短路

31. 最小生成树

31. 有向图的强连通分量

32. 无向图的双连通分量

33. 二分图的最大匹配

34. 叉积/点与线段/线段与线段

35. 组合

36. Catalan Number

37. 通项公式