RECE: Reduced Cross-Entropy Loss for Large-Catalogue Sequential Recommenders

Danil Gusak*, Gleb Mezentsev*, Ivan Oseledets, Evgeny Frolov

[Paper] [BibTeX]

Scalability is a major challenge in modern recommender systems. In sequential recommendations, full Cross-Entropy (CE) loss achieves state-of-the-art recommendation quality but consumes excessive GPU memory with large item catalogs, limiting its practicality. Using a GPU-efficient locality-sensitive hashing-like algorithm for approximating large tensor of logits, this paper introduces a novel RECE (REduced Cross-Entropy) loss. RECE significantly reduces memory consumption while allowing one to enjoy the state-of-the-art performance of full CE loss. Experimental results on various datasets show that RECE cuts training peak memory usage by up to 12 times compared to existing methods while retaining or exceeding performance metrics of CE loss. The approach also opens up new possibilities for large-scale applications in other domains.

Requirements Installation

To install all the necessary packages, simply run

conda env create -f environment.yml
conda activate rce

Experiments Reproduction

When running the code for the experiments, you can pass a +project_name={PNAME} +task_name{TNAME} option, in which case the intermediate validation metrics and the final test metrics will be reported to a ClearML server and could be later viewed in a web interface, otherwise only the final test metrics will be printed to the terminal.

Impact of different components on peak GPU memory when training SASRec with Cross-Entropy loss

To generate the data used for the corresponding plot, you should run the following command with the required parameter values:

python measure_ce_memory.py --bs={BS} --catalog={CATALOG_SIZE}

Model Performance Under Memory Constraints & Evaluating SASRec-RECE Against Contemprorary Models

To reproduce the best results from the paper (in terms of NDCG@10) for each model ($RECE$, $BCE$, $gBCE$, $CE^-$, $CE$), you should run the following command

python train.py --config-path={CONFIG_PATH} --config-name={CONFIG_NAME} data_path={DATA_PATH}

For example, to reproduce the best results of the $CE$ model on the Yelp dataset with temporal train/test splitting, you should run

python train.py --config-path=configs/temporal/gowalla --config-name='ce' data_path=data/gowalla.csv

For the $RECE$ model on Gowalla there are both configs for the best NDCG@10 performance (rece_max_ndcg.yaml) and for the same performance as the second best model but with a reduced memory consumption (rece_same_ndcg.yaml).

To reproduce the result for non-optimal configurations (other points on the corresponding figure) and to reproduce more accurate results for optimal configurations (using several random seeds), you should perform the grid search on relevant hyperparameters for each model and modify the configs accordingly. The grid used is shown below:

{
    "ce": 
        {"trainer_params.seed": [1235, 37, 2451],
         "dataloader.batch_size": [4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096]},
    "bce": 
        {"trainer_params.seed": [1235, 37, 2451],
         "dataloader.batch_size": [4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096],
         "dataloader.n_neg_samples": [1, 4, 16, 64, 256, 1024, 4096]},
    "dross(CE^-)": 
        {"trainer_params.seed": [1235, 37, 2451],
         "dataloader.batch_size": [4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096],
         "dataloader.n_neg_samples": [1, 4, 16, 64, 256, 1024, 4096]},
    "gbce": 
        {"trainer_params.seed": [1235, 37, 2451],
         "dataloader.batch_size": [4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096],
         "dataloader.n_neg_samples": [1, 4, 16, 64, 256, 1024, 4096],
         "model_params.gbce_t": [0.75, 0.9]},
    "rece": 
        {"trainer_params.seed": [1235, 37, 2451],
         "dataloader.batch_size": [4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096],
         "model_params.n_buckets": "int((4. * (1 + 2 * model_params.n_extra_chunks) * min(catalog_size, dataloader.batch_size * interactions_per_user)) ** 0.5)",
         "model_params.n_extra_chunks": [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
         "model_params.rounds": [1, 2, 4, 8, 16, 32, 64, 128]},
}

The parameters of the underlying transformer are selected accoring to the original SASRec work, were the same in all the experiments (except the leave_one_out split experiments) and could be seen in any of the config files.

Optimal bucket size

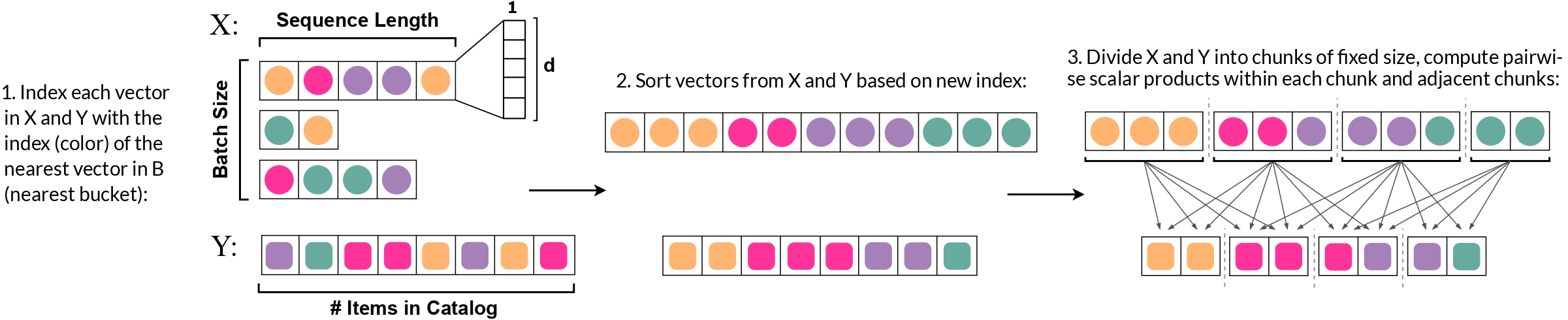
For all experiments presented in the paper an optimal in the following sense bucket size was selected. There are three possible memory bottlenecks of our algorithm, depending on data and model parameters. The first two bottlenecks are storing the projections of $X$ and $Y$ onto $B$, which are later used for bucket assigment.

 with torch.no_grad():
    x_bucket = buckets @ x.T # (rounds, n_b, hd) x (hd, bs) -> (rounds, n_buckets, bs)
    x_ind = torch.argsort(torch.argmax(x_bucket, dim=1)) # (rounds, bs)
    del x_bucket

    y_bucket = buckets @ w.T # (rounds, n_b, hd) x (hd, ds) -> (rounds, n_buckets, ds)
    y_ind = torch.argsort(torch.argmax(y_bucket, dim=1)) # (rounds, ds)
    del y_bucket, buckets

As they are calculated in "no_grad" mode and deleted right after the assignment indices are calculated, the peak memory usage of our loss function at the moment after index assignment is $max(r \cdot n_b \cdot s \cdot l, r \cdot n_b \cdot C)$, where $s$ is a batch size, $l$ is a sequence length, $C$ is a catalog size, $r$ is a number of rounds and $n_b$ is a number of buckets.

The third potential bottleneck is calculating the number of duplicate pairs within chunks over rounds.

catalog = torch.take_along_dim(catalog, y_ind.view(-1), 0) \
    .view(self.rounds, n_chunks, chunk_size_y) # is needed for accounting for duplicates when rounds > 1
catalog = F.pad(catalog, 
                (0, 0, self.n_extra_chunks, self.n_extra_chunks),
                'constant', self.pad_token) # (rounds, n_chunks+n_extra_chunks*2, chunk_size_y)
catalog = catalog.unfold(1, n_chunks, 1) \
                    .permute(0, 3, 1, 2) \
                    .view(self.rounds, n_chunks, -1) # (rounds, n_chunks, (1+2*n_extra_chunks) * chunk_size_y)
catalog_ = \
    catalog[:, :, None, :] \
        .expand(-1, -1, chunk_size_x, -1) \
        .reshape(catalog.shape[0], -1, catalog.shape[-1]) 
        # (rounds, n_chunks * chunk_size_x, (1+2*n_extra_chunks) * chunk_size_y)
catalog = torch.zeros_like(catalog_) \
                .scatter_(1, x_ind[:, :, None] \
                .expand_as(catalog_), catalog_) 
                # same shape, but now ordered as originally, before it was ordered according to chunks
catalog = catalog.permute(1, 0, 2) \
                    .reshape(catalog.shape[1], -1) 
                    # (n_chunks * chunk_size_x, rounds * (1+2*n_extra_chunks) * chunk_size_y))
catalog_sorted = torch.sort(catalog)[0]
catalog_counts = torch.searchsorted(catalog_sorted, catalog, side='right', out_int32=True)
catalog_counts2 = torch.searchsorted(catalog_sorted, catalog, side='left', out_int32=True)
del catalog_sorted
catalog_counts -= catalog_counts2

We utilized torch.seachsorted function for duplicates calculation, which results in storing 4 tensors of the same size (catalog, catalog_sorted, catalog_counts, catalog_counts2) right before the duplicates are counted. The total size of the occupied memory for these tensors is $4\cdot r \cdot n_c \cdot c_x \cdot c_y \cdot (1+2n_{ec})$, where $n_c$ is the number of chunks, $c_x$ is the number of elements from the input sequence in chunk, $c_y$ is the number of elements from the catalog in chunk and $n_{ec}$ is the number of neighboring chunks we look into. If we take into account that $c_x=(s\cdot l) / n_c$, $c_y = C / n_c$ and $n_c = n_b / \alpha_{bc}$, then the peak memory is $(4 \cdot r \cdot s \cdot l \cdot C \cdot (1+2n_{ec}) \cdot \alpha_{bc}) / n_b$.

As the number of buckets grow, the reduction in memory required to store the logits tensor (as well as duplicate counts tensor), increases, as the logits are only caclulated only inside buckets, and more buckets mean smaller buckets. However, if the number of buckets is too large, then calculating and storing projections of $X$ and $Y$ becomes more expensive than the calculation of the logits itself.

So we want to balance these contributions, by finding the corresponding value of $n_b$.

$$n_b^* \cdot r \cdot max(\cdot s \cdot l, C) = (4 \cdot r \cdot s \cdot l \cdot C \cdot (1+2n_{ec}) \cdot \alpha_{bc}) / n_b^*$$

$$n_b^* = \sqrt{4\cdot \alpha_{bc} \cdot min(s\cdot l, C) \cdot (1+2n_{ec})}$$

Then, the total memory complexity is $2 r\sqrt{\alpha_{bc} (1+2 n_{ec}) \cdot \min(C, s\cdot l)} \cdot \max(C, s\cdot l)$.

Citing RECE

Please use the following BibTeX entry:

@article{gusak2024rece,
  title={RECE: Reduced Cross-Entropy Loss for Large-Catalogue Sequential Recommenders},
  author={Gusak, Danil and Mezentsev, Gleb and Oseledets, Ivan and Frolov, Evgeny},
  journal={arXiv preprint arXiv:2408.02354},
  year={2024}
}