This repository contains a OpenFHE-based project that implements an encrypted version of the ResNet20 model, used to classify encrypted CIFAR-10 images.
The reference paper for this work is Encrypted Image Classification with Low Memory Footprint using Fully Homomorphic Encryption.
The key idea behind this work is to propose a solution to run a CNN in relative small time (
De Castro et al. [6] showed that memory is currently the main bottleneck to be addressed in FHE circuits, although most of the works do not consider it as a metric when building FHE solutions.
Existing works use a lot of memory ([4]:
The circuit is based on the RNS-CKKS implementation [1] in OpenFHE [2]. We propose an approach to convolutions called Optimized Vector Encoding, which enabled to evaluate a convolution using only five Automorphism Keys, needed to rotate the values of the ciphertext. These are the heaviest objects in memory, therefore by minimizing the use of these keys, it is possible to reduce the memory footprint of the application.
Experiments show that it is possible to evaluate the circuit in less than 5 minutes (in [3] it requires more than 6 minutes) and by using a small amount of RAM, from 10GB to 15GB, depending on the desired precision and speed.
The program simulates a server-client interaction in which the server is assumed to be honest-but-curious.
Both client and server agree on a pair public-secrey key that is based on Ring Learning With Errors (RLWE) [3]: a post-quantum hard problem defined as follows:
Given a polynomial ring
- Secret key:
$s \gets \chi$ is a polynomial with random coefficients in$\mathcal{R}$ - Public key:
$(a, b)$ , where$a$ is a random polynomial in$\mathcal{R}$ , and$b = a \cdot s + e$ , with$e \gets \chi$
The idea is to use
- The client encrypts the image using the public key.
- The server performs computations on it (following the definition of Fully Homomorphic Encryption)
- The server returns an encrypted vector containing the output of the last fully connected layer. The client is able to decrypt it and see the result
- The client finds the index of the maximum value and, using a dictionary, find the classified label
Linux or Mac operative system, with at least 16GB of RAM.
In order to run the program, you need to install:
cmakeg++orclangOpenFHE(how to install OpenFHE)
Setup the project using this command:
mkdir build
cmake -B "build" -S LowMemoryFHEResNet20
Then build it using
cmake --build "build" --target
After building, go to the created build folder:
cd build
and run it with the following command:
./LowMemoryFHEResNet20
generate_keys, typeint, a value in[1, 2, 3, 4]load_keys, type:inta value in[1, 2, 3, 4]input, type:string, the filename of a custom image. MUST be a three channel RGB 32x32 image either in.jpgor in.pngformatverbosea value in[-1, 0, 1, 2], the first shows no information, the last shows a lot of messagesplain: added when the user wants the plain result too. Note: enabling this option means that a Python script will be executed after the encrypted inference. This script requires the following modules:torch,torchvision,PIL,numpy.
The first execution should be launched with the generate_keys argument, using the preferred set of parameters. Check the paper to see the differences between them. For instance, we choose the set of parameters defined in the first experiment:
./LowMemoryFHEResNet20 generate_keys 1
This command create the required keys and stores them in a new folder called keys_exp1, in the root folder of the project.
The default command creates a new context and classifies the default image in inputs/luis.png. We can, however, use custom arguments.
We can use a set of serialized context and keys with the argument load_keys as follows:
./LowMemoryFHEResNet20 load_keys 1
This command loads context and keys from the folder keys_exp1, located in the root folder of the project, and runs an inference on the default image.
Then, in order to load a custom image, we use the argument input as follows:
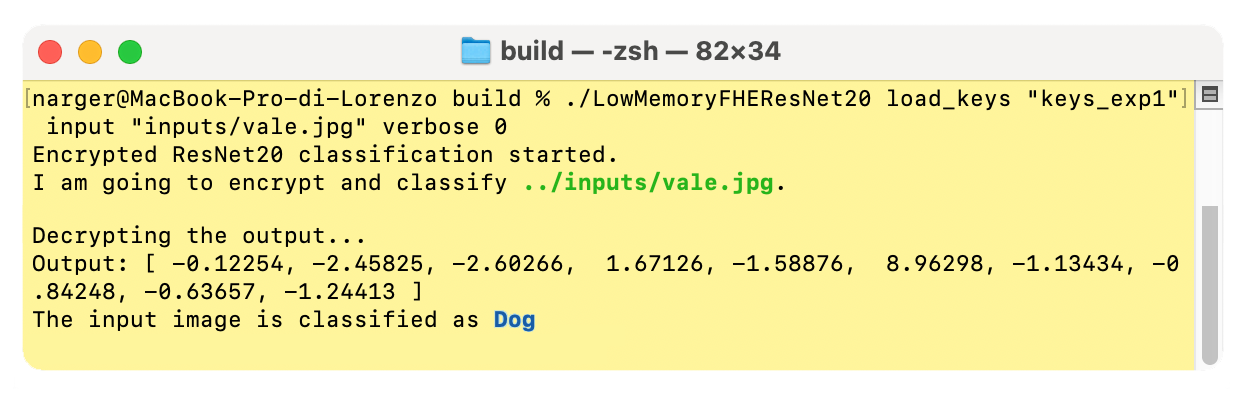
./LowMemoryFHEResNet20 load_keys 1 input "inputs/vale.jpg"
Even for this argument, the starting position will be the root of the project.
We can also compare the result with the plain version of the model, using the plain keyword:
./LowMemoryFHEResNet20 load_keys 1 input "inputs/vale.jpg" plain
This command will launch a Python script at the end of the encrypted comptations, giving the plain output (which will differ from the encrypted one according to the parameters, check the paper for the precision values of each set of parameters).
Notice that plain requires a few things in order to be used:
python3torchtorchvisionPILnumpy
The output of the encrypted model is a vector consisting of 10 elements. In order to interpret it, it is enough to find the index of the maximum element. A sample output could be:
output = [-2.633, -1.091, 6.063, -4.093, -0.5967, 7.252, -2.156, -1.085, -0.9119, -0.7291]
In this case, the maximum value is at position 5. Just translate it using the following dictionary (from ResNet20 pretrained on CIFAR-10):
| Index of max | Class |
|---|---|
| 0 | Airplane |
| 1 | Automobile |
| 2 | Bird |
| 3 | Cat |
| 4 | Deer |
| 5 | Dog |
| 6 | Frog |
| 7 | Horse |
| 8 | Ship |
| 9 | Truck |
In the sample output, the input image was my dog Vale:
Another output could be
output = [-0.719, -4.19, -0.252, 12.04, -4.979, 4.413, -0.5173, -1.038, -2.229, -2.504]
In this case, the index of max is 3, which is nice, since the input image was Luis, my brother's cat:
So it was correct!
In the notebook folder, it is possible to find different useful notebooks that can be used in order to compute the precision of a computation, with respect to the plain model, in details for each layer.
- Lorenzo Rovida (
lorenzo.rovida@unimib.it) - Alberto Leporati (
alberto.leporati@unimib.it)
Made with <3 at Bicocca Security Lab, at University of Milan-Bicocca.
This is a proof of concept and, even though parameters are created with
[1] Kim, A., Papadimitriou, A., & Polyakov, Y. (2022). Approximate Homomorphic Encryption with Reduced Approximation Error*. In: Galbraith, S.D. (eds) Topics in Cryptology – CT-RSA 2022. CT-RSA 2022. Lecture Notes in Computer Science, vol 13161. Springer, Cham.
[2] Al Badawi, A., Bates, J., Bergamaschi, F., Cousins, D. B., Erabelli, S., Genise, N., Halevi, S., Hunt, H., Kim, A., Lee, Y., Liu, Z., Micciancio, D., Quah, I., Polyakov, Y., R.V., S., Rohloff, K., Saylor, J., Suponitsky, D., Triplett, M., Zucca, V. (2022). OpenFHE: Open-Source Fully Homomorphic Encryption Library. Proceedings of the 10th Workshop on Encrypted Computing & Applied Homomorphic Cryptography, 53–63.
[3] Lyubashevsky, V., Peikert, C., & Regev, O. (2010). On Ideal Lattices and Learning with Errors over Rings. In: Gilbert, H. (eds) Advances in Cryptology – EUROCRYPT 2010. EUROCRYPT 2010. Lecture Notes in Computer Science, vol 6110. Springer, Berlin, Heidelberg.
[4] Kim, D., & Guyot, C. (2023). Optimized Privacy-Preserving CNN Inference With Fully Homomorphic Encryption. In IEEE Transactions on Information Forensics and Security, vol. 18, pp. 2175-2187.
[5] Lee, E., Lee, J. W., Lee, J., Kim, Y. S., Kim, Y., No, J. S., & Choi, W. (2022, June). Low-complexity deep convolutional neural networks on fully homomorphic encryption using multiplexed parallel convolutions. In International Conference on Machine Learning (pp. 12403-12422). PMLR.
[6] De Castro, L., Agrawal, R., Yazicigil, R., Chandrakasan, A., Vaikuntanathan, V., Juvekar, C., & Joshi, A. (2021). Does Fully Homomorphic Encryption Need Compute Acceleration?