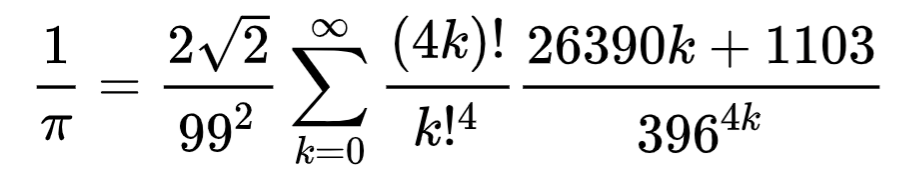Computing π w/ Ramanujan-Sato

Introduction

Srinivasa Ramanujan (1887-1920) is one of history’s most gifted Mathematicians, sadly departing before he was even 33 years of age.

In 1917 Srinivasa discovered several formulas for π. The one below is known as the “Ramanujan-Sato Series”:

The incredible thing about this formula is its exponential speed of convergence (the tree large terms simplify to O((99^(-4k)*k^(-3/2)) for large k). In turn, the ratios must be at least the precision we would like to approximate π with. Below we show the growth of the three large terms in the series, and the exponent of their product, for k=1 to 5:

k	t1=(4k)!	t2=(k!)^4	t3=396^(4k)	O[t1/(t2*t3)]
1	2.400000e+01	1	2.459126e+10	-9
2	4.032000e+04	16	6.047300e+20	-17
3	4.790016e+08	1296	1.487107e+31	-26
4	2.092279e+13	331776	3.656983e+41	-34
5	2.432902e+18	207360000	8.992982e+51	-42

Notice that for small k, (396^(4k)) grows fastest, though above a certain k factorials will take over, k! ~ O(k^k).

53-bit doubles in R are limited to 22 significant digits. So for k>2, this term will be truncated. Take k=4 as an example:

print(396^(4*4),digits=22)
#> [1] 3.6569832807775449e+41

Via the arbitrary-precision Rmpfr package (using 120 bits), we can see the above with its full 42 digits:

Rmpfr::mpfr(396, 120)^(4*4)
#> 1 'mpfr' number of precision  120   bits 
#> [1] 365698328077754498546241794891999342493696

Total integer precision is imperative in the series computation, so we start by loading the arbitrary-precision library.

Load the arbitrary-precision library

We will be using 240 bits of precision:

library(dplyr) # to use "%>%" and "tibble"
library(Rmpfr) # use this for arbitrary-precision floats
bits <- 240

One term of the R-S series and its front coefficient:

sqrt2 <- sqrt(mpfr("2", bits))
rs_coeff <- 9801L/(2L*sqrt2)

rs_term <- function(k) {
  num <- factorial(4L*k)*(26390L*k+1103L)
  den <- (factorial(k)*(396L^k))^4L
  num/den
}

Computes π w/ kmax iterations of the R-S formula (reciprocal of original formula):

rs_series <- function(kmax) {
  terms <- rs_term(mpfr(0:(kmax-1),bits))
  (rs_coeff/cumsum(terms))
}

Calculate π

Only 5 iterations and we’re pretty close:

rs_series(5)
#> 5 'mpfr' numbers of precision  240   bits 
#> [1] 3.141592730013305660313996189025215518599581607110033559656536290128551455
#> [2]   3.1415926535897938779989058263060130942166450293228488791739637915057844
#> [3] 3.141592653589793238462649065702758898156677480462334781168399595644739792
#> [4] 3.141592653589793238462643383279555273159974210420379911216703896006945788
#> [5] 3.141592653589793238462643383279502884197663818133030623976165590998553105

Obtains high-precision π computed internally by mpfr package:

piMpfr <- Const("pi",bits)
piMpfr
#> 1 'mpfr' number of precision  240   bits 
#> [1] 3.141592653589793238462643383279502884197169399375105820974944592307816407

Order of error vs iteration, notice we are expanding the accuracy by 8 digits per iteration:

iter	error	newDigits
1	-7	NA
2	-15	8
3	-23	8
4	-31	8
5	-39	8

Mind-blowing convergence to the value of π afforded by the Ramanujan-Sato series! 😄

References:

N. Baruah, B. Berndt, H. Chan, “Ramanujan’s Series for 1/π: A Survey”, Mathematical Association of America, Aug-Sept 2009. pdf
Wikipedia, “Srinivasa Ramanujan”
M. Mächler, “Arbitrarily Accurate Computation with R: The Rmpfr Package”, ETH Zurich, 2019. pdf

dan-reznik/Ramanujan-Sato

Computing π w/ Ramanujan-Sato

Introduction

Load the arbitrary-precision library

Calculate π

References: