ConvexPolygon Calculator is an application to operate with convex polygons.
ConvexPolygon Calculator is an interactive application whose objective is to give the user a tool to operate with polygons in an easy and visual way, since this application includes a polygon plotter. The code of the calculator is open, so you can add new utilities to the application in order to make it more useful for you objectives.
In order to install the ConvexPolygon Calculator, you have to do the following, depending on which Operative System you are using:
- For Linux and iOS:
-
Install the PngWriter library, in order to be able to draw your polygons. More info about the download in it's github repository: https://github.com/pngwriter/pngwriter
-
Download the folder with all it's containing files and execute the command make in your command line executer.
- For Windows : ⋅⋅⋅It is not supported, although it might work making some small modifications.
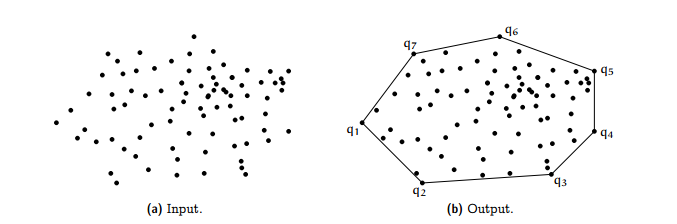
A convex polygon is a simple polygon in which all its interior angles are strictly less than 180°, as you can see in the following example.
A polygon has n vertices and n edges and is said to be regular when all edges have the same length.
In our application, the convex polygons are implemented through the ConvexPolygon class., which defines a convex polygon as a vector of points, and these are represented by the Cartesian Coordinates (x,y).
Now, we are going to define some utilities that can be done with Convex Polygons, including operations between them, and usefull information we can ask about.
- Convex Hull: Given a set of points, we can calculate the smallest convex polygon that contains the set.
- Convex Union: Given two convex polygons, the convex union is the smallest convex polygon that contains both polygons. Equivalently, it is the convex hull of both polygons.
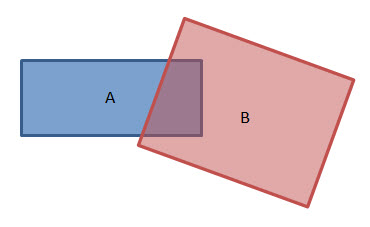
- Intersection: The intersection of two convex polygons is a convex polygon.
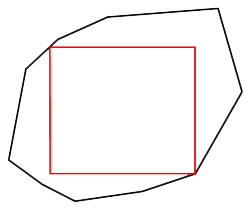
- Bounding Box: Given a set of convex polygons, find the smallest bounding box that encloses all polygons.
- Inside: We can check whether a convex polygon is inside another convex polygon.
- Number of vertices and edges
- Length of the perimeter
- Area
- Coordinates of the centroid
For convenience, we will consider some particular cases of polygons (not always recognized as polygons by mathematicians):
- Empty polygon: a polygon with zero vertices.
- Monogon: a polygon with one vertex (a point).
- Digon: a polygon with two vertices (a segment).
The calculator consists on a command line reader which will play the following commands, some of which results have been explained in the previous sections. Each command produces a line of output.
Using the iostream library, the program must read and write in the console like in the following example.
Given a example.txt text file which contains:
pentagon1 9 35 31 35 38 14 20 1 2 14
triangle1 2 14 38 14 19 35
The output(right column), from the left input should look like this:
|# Example test for ConvexPolygon Calculator |# |
|# Now we create a square |# |
|# and we explore its properties |# |
|polygon p1 0 0 2 0 2 2 0 2 |ok |
|vertices p1 |4 |
|perimeter p1 |8.000 |
|area p1 |4.000 |
|centroid p1 |1.000 1.000 |
|print p1 |p1 0.000 0.000 2.000 0.000 2.000 2.000 0.000 2.000 |
|# now we load from the file example_test.txt|# |
|load example_test.txt |ok |
|list |p1 pentagon1 triangle1 |
|inside pentagon1 triangle1 |no |
|inside triangle1 pentagon1 |yes |
|bbox p3 pentagon1 triangle1 |ok |
|print p3 |p3 2.000 1.000 38.000 1.000 38.000 35.000 2.000 35.000|
|setcol triangle1 0 0 1 |ok |
|setcol pentagon1 1 0 0 |ok |
|draw image.png pentagon1 triangle1 |ok |
|save polygons_data.txt |ok |
|--------------------------------------------|------------------------------------------------------|
, where the resulting image.png should look like the following one:
and the polygons_data.txt should be like this:
p3 2.000 14.000 2.000 14.000 9.000 35.000 31.000 35.000 38.000 14.000 20.000 1.000
pentagon1 9.000 35.000 31.000 35.000 38.000 14.000 20.000 1.000 2.000 14.000
triangle1 2.000 14.000 38.000 14.000 19.000 35.000
Points in the commands are given by two pairs of real numbers, in standard notation, to denote the X and Y coordinates. For instance, 0 0 or 3.14 -5.5. When printed, all real numbers must be formatted with three digits after the decimal dot.
All commands include polygon identifiers. These are made by words, such as p, p1, p2, or pol_gr.
Lines starting with a hash sign (#) are comments. Their output is just a hash sign.
Colors in the commands are given by three real numbers in [0,1], in standard notation, to denote the RGB color. For instance, 0 0 0 denotes black, 1 0 0 denotes red, and 1 0.64 0 denotes orange.
Filenames in the commands are made up of words, such as f, pol.txt or some_file_name.pol.
The polygon command associates an identifier with a convex polygon made by a set of zero or more points. If the polygon identifier is new, it will create it. If it already existed, it will overwrite the previous polygon. New polygons are black.
print command prints the name and the vertices of a vertices of a given polygon. The output must only contain the vertices in the convex hull of the polygon, in clockwise order, starting from the vertex will lower X (and the vertex with lower Y in case of ties). They must be printed in a single line, with one space separating each value.
The area command prints the area of the given polygon.
The perimeter command prints the perimeter of the given polygon.
The vertices command prints the number of vertices of the convex hull of the given polygon.
The centroid command prints the centroid of the given polygon.
The list command lists all polygon identifiers, lexycographically sorted.
The save command saves the given polygons in a file, overwriting it if it already existed. The contents of the file must be the same as in the print command, with a polygon per line.
The load command loads the polygons stored in a file, in the same way as polygon, but retrieving the vertices and identifiers from the file.
The setcol command associates a color to the given polygon.
The draw command draws a list of polygons in a PNG file, each one with its associated color. The image should be of 500x500 pixels, with white background and the coordinates of the vertices should be scaled to fit in the 498x498 central part of the image, while preserving the original aspect ratio.
This command may receive two or three parameters:
-
When receiving two parameters p1and
p2,p1should be updated to the intersection of the originalp1andp2. -
When receiving three parameters
p1,p2andp3,p1should be updated to the intersection ofp2andp3.
Take into account that identifiers may be repeated.
Just as the intersection command, but with the convex union of polygons.
Given two polygons, the inside command prints yes or no to tell whether the first is inside the second or not.
The bbox command creates a new polygon with the four vertices corresponding to the bounding box of the given polygons.
As seen in the examples, some commands do not really produce an answer. In this case ok must be printed, unless there was some error.