Hyperparameter tuning relates to how we sample candidate model architectures from the space of all possible hyperparameter values. This is often referred to as searching the hyperparameter space for the optimum values. In this lesson we'll look at some of the key hyper parameters for Decision Trees and how they affect the learning and prediction processes.
- Understand and explain the role of hyperparameter optimization in machine learning
- Identify the role of pruning while training a decision tree
- Understand and explain key pruning parameters that can affect the predictive performance of decision trees
In machine learning, a hyperparameter is a parameter whose value is set before the learning process begins.
By contrast, the values of model parameters are derived via training as we have seen previously. Different model training algorithms require different hyperparameters, some simple algorithms (such as ordinary least squares regression) require none. Given these hyperparameters, the training algorithm learns the parameters from the data. For instance, LASSO is an algorithm that adds a regularization hyperparameter to ordinary least squares regression, which has to be set before estimating the parameters through the training algorithm.
In this lesson we shall look at such optimizations in context of decision trees and see how these can effect the predictive performance as well the computational complexity of the tree.
Now that we know how to grow a decision tree using python and scikit learn, let's move on and practice with the idea of Optimization of the classifer. This means that we have some options available with decision trees that we can tweak before the actual learning takes place.
A decision tree , grown beyond a certain level of complexity leads to over-fitting. If we grow our tree and carry on using poor predictors which dont have any impact on the accuracy will eventually a) slow down the learning, and b) cause overfitting.
This process of trimming decision trees to optimize the learning process is called "Tree Pruning".
We can prune our trees using the following parameters:
Maximum Depth
Reduce the depth of the tree to build a generalized tree. Set the depth of the tree to 3, 5, 10 depending after verification on test data
Minimum Samples Leaf with Split
Restrict the size of sample leaf
Minimum Leaf Sample Size
Size in terminal nodes can be fixed to 30, 100, 300 or 5% of total
Maximum Leaf Nodes
Reduce the number of leaf nodes
Maximum Features
Maximum number of features to consider when splitting a node
Below we shall look at a selected hyper parameters and learn about their impact of the classifier performance.
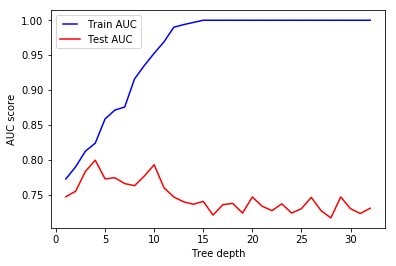
The parameter for decision trees that we normally tune first is max_depth. This parameter indicates how deep we want our tree to be. IF the tree is too deep, it means we are creating a large number of splits in the parameter space and capturing more information about underlying data. This may result as overfitting as we are learning granular information from given data , we make it difficult for our model to generalize for unseen data. This will result as a low training error but a large testing error.
If, on the other hand, the tree is too shallow, we may run into underfitting, i.e. we are not learning enough information about the data and the accuracy of model stays low for both test and training samples . We fit a decision tree with depths ranging from 1 to 32 and plot the training and test auc scores.
In above example, we see that as the tree depth increases, our validation/test accuracy starts to go down after a depth of around 4. But with even greater depths, the training accuracy keeps on rising , as the classifer learns more information from the data , but this can not be mapped onto unseen examples, hence the validation accuracy falls down constantly. Finding the sweet spot (e.g. depth=4) in this case would be the first hyper parameter that we need to tune.
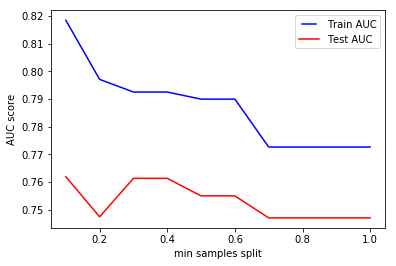
The hyper parameter min_samples_split is used to set the minimum number of samples required to split an internal node. This can vary between two extremes i.e. considering only one sample at each node vs. considering all of the samples at each node - for a given attribute.
When we increase this parameter value, the tree becomes more constrained as it has to consider more samples at each node. Here we will vary the parameter from 10% to 100% of the samples.
In the above plot, we see that the training and testing accuracy stabilize at certain min. sample split size , and stays the same even if we carry on increasing the size of the split. This means that we will have a complex model, with similar accuracy that a much simpler model could potentially exhibit. Therefore, it is imperative that we try to identify the optimal sample size during the training phase.
max_dapth and min_samples+splt are also both related to the computational cost involved with growing the tree. nLarge values for these parameters can create a complex, dense and long tree and with large datasets, it may become extremely time consuming to use default values.
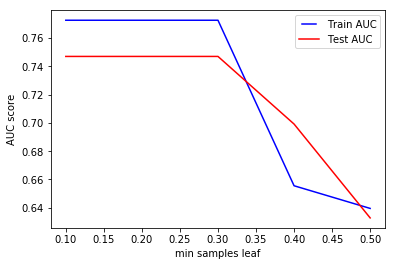
This hyper parameter is used to identify the minimum number of samples that we want a leaf node to contain. When this minimum size is achieved at a node, it does not get split any further. This parameter is similar to min_samples_splits, however, this describe the minimum number of samples of samples at the leafs, the base of the tree.
Above shows the impact of this parameter on the accuracy of the classifier. We see that increasing this parameter value after an optimal point results as a drop in accuracy. That is due to under-fitting again, as keeping too many samples in our leaf nodes mean that there is still a high level of uncertainty in the data.
The main difference between the two is that min_samples_leaf guarantees a minimum number of samples in a leaf, while min_samples_split can create arbitrary small leaves, though min_samples_split is more common in practice. These two hyper parameters make the distinction between a leaf (terminal/external node) and an internal node. An internal node will have further splits (also called children), while a leaf is by definition a node without any children (without any further splits).
For instance, if min_samples_split = 5, and there are 7 samples at an internal node, then the split is allowed. But let's say the split results in two leaves, one with 1 sample, and another with 6 samples. If min_samples_leaf = 2, then the split won't be allowed (even if the internal node has 7 samples) because one of the leaves resulted will have less then the minimum number of samples required to be at a leaf node.
In addition of above, Scikit Learn offers a number of other parameters for further fine tuning the learning process. Consult the official doc to look at these parameters in detail. The parameters mentioned here are directly related to the complexity which may arise in decision trees and are normally tuned when growing trees. We shall shortly see this in action with a real dataset.
In this lesson, we looked at the idea of hyper parameters optimization and how pruning plays an important role in restricting the growth of a decision tree , for our predictions to be accurate. We looked at a few hyper parameters which directly impact the potential over-fitting/underfitting in trees. Next we shall see these in prctice using scikit learn and python.