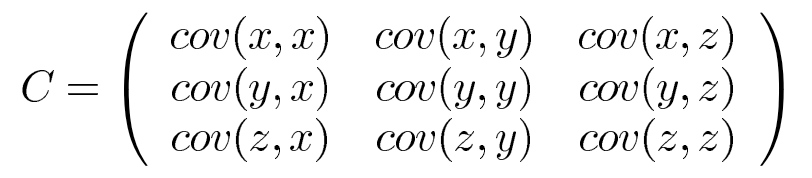In this lesson, we shall look at some background concepts required to understand how PCA works, with required mathematical formulas and python implementation. We shall look at covariance matrix, Eigen decomposition and will work with required numpy functions.
You will be able to:
- Understand covariance matrix calculation with implementation in numpy
- Understand and explain Eigendecomspoistion with its basic characteristics
- Explain the role of eigenvectors and eigenvalues in eigendecomposition
- Decompose and re-construct a matrix using eigendecomposition
We have looked into correlation and covariance as measures to calculate how one random variable changes with respect to another. Covariance is always measured between 2 dimensions (variables).
If we calculate the covariance between a dimension and itself, we get the variance.
So, if we a 3-dimensional data set (x, y, z), then we can measure the covariance between the x and y dimensions, the y and z dimensions, and the x and z dimensions. Measuring the covariance between x and x, or y and y, or z and z would give us the variance of the x, y and z dimensions respectively.
The formula for covariance is give as:
We know that covariance is always measured between 2 dimensions only. If we have a data set with more than 2 dimensions, there is more than one covariance measurement that can be calculated. For example, from a 3 dimensional data set (x, y, z) you could calculate cov(x,y), cov(x,z), and cov(y,z).
For an -dimensional data set, we can calculate $ \frac{n!}{(n-2)! * 2}$different covariance values.
A useful way to get all the possible covariance values between all the different dimensions is to calculate them all and put them in a matrix. The covariance matrix for a set of data with n dimensions would be:
where
So if we have an n-dimensional data set, then the matrix has n rows and n columns (square matrix) and each entry in the matrix is the result of calculating the covariance between two separate dimensions as shown below:
-
Down the main diagonal, we can see that the covariance value is between one of the dimensions and itself. These are the variances for that dimension.
-
Since
$cov(a,b) = cov(b,a)$ , the matrix is symmetrical about the main diagonal.
In numpy, we can calculate the covariance of a given matrix using np.cov() function, as shown below:
# Covariance Matrix
import numpy as np
X = np.array([ [0.1, 0.3, 0.4, 0.8, 0.9],
[3.2, 2.4, 2.4, 0.1, 5.5],
[10., 8.2, 4.3, 2.6, 0.9]
])
print( np.cov(X) )# Code here [[ 0.115 0.0575 -1.2325]
[ 0.0575 3.757 -0.8775]
[-1.2325 -0.8775 14.525 ]]
The diagonal elements,
print(np.var(X, axis=1, ddof=1))# Code here [ 0.115 3.757 14.525]
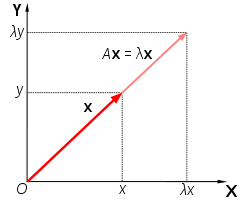
The eigendecomposition is one form of matrix decomposition. Decomposing a matrix means that we want to find a product of matrices that is equal to the initial matrix. In the case of the eigendecomposition, we decompose the initial matrix into the product of its eigenvectors and eigenvalues.
A vector
Here, lambda (
A matrix can have one eigenvector and eigenvalue for each dimension of the parent matrix.
Also , remember that not all square matrices can be decomposed into eigenvectors and eigenvalues, and some can only be decomposed in a way that requires complex numbers. The parent matrix can be shown to be a product of the eigenvectors and eigenvalues.
A decomposition operation breaks down a matrix into constituent parts to make certain operations on the matrix easier to perform. Eigendecomposition is used as an element to simplify the calculation of other more complex matrix operations.
Eigenvectors are unit vectors, with length or magnitude is equal to 1.0. They are often referred as right vectors, which simply means a column vector (as opposed to a row vector or a left vector). Imagine a transformation matrix that, when multiplied on the left, reflected vectors in the line
Eigenvalues are coefficients applied to eigenvectors that give the vectors their length or magnitude. For example, a negative eigenvalue may reverse the direction of the eigenvector as part of scaling it. Eigenvalues are closely related to eigenvectors.
A matrix that has only positive eigenvalues is referred to as a positive definite matrix, whereas if the eigenvalues are all negative, it is referred to as a negative definite matrix.
Decomposing a matrix in terms of its eigenvalues and its eigenvectors gives valuable insights into the properties of the matrix. Certain matrix calculations, like computing the power of the matrix, become much easier when we use the eigendecomposition of the matrix. The eigendecomposition can be calculated in NumPy using the eig() function.
The example below first defines a 3×3 square matrix. The eigendecomposition is calculated on the matrix returning the eigenvalues and eigenvectors using eig() method.
# eigendecomposition
from numpy import array
from numpy.linalg import eig
# define matrix
A = array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(A)
# calculate eigendecomposition
values, vectors = eig(A)
print(values)
print(vectors)# Code here [[1 2 3]
[4 5 6]
[7 8 9]]
[ 1.61168440e+01 -1.11684397e+00 -9.75918483e-16]
[[-0.23197069 -0.78583024 0.40824829]
[-0.52532209 -0.08675134 -0.81649658]
[-0.8186735 0.61232756 0.40824829]]
Above, The eigenvectors are returned as a matrix with the same dimensions as the parent matrix (3x3), where each column is an eigenvector, e.g. the first eigenvector is vectors[:,0]. Eigenvalues are returned as a list, where value indices in the returned array are paired with eigenvectors by column index, e.g. the first eigenvalue at values[0] is paired with the first eigenvector at vectors[: 0].
We will now test whether the first vector and value are in fact an eigenvalue and eigenvector for the matrix. We know they are, but it is a good exercise.
# confirm first eigenvector
B = A.dot(vectors[:, 0])
print(B)
C = vectors[:, 0] * values[0]
print(C)# Code here [ -3.73863537 -8.46653421 -13.19443305]
[ -3.73863537 -8.46653421 -13.19443305]
We can reverse the process and reconstruct the original matrix given only the eigenvectors and eigenvalues.
First, the list of eigenvectors must be converted into a matrix, where each vector becomes a row. The eigenvalues need to be arranged into a diagonal matrix. The NumPy diag() function can be used for this. Next, we need to calculate the inverse of the eigenvector matrix, which we can achieve with the inv() function. Finally, these elements need to be multiplied together with the dot() function.
from numpy.linalg import inv
# create matrix from eigenvectors
Q = vectors
# create inverse of eigenvectors matrix
R = inv(Q)
# create diagonal matrix from eigenvalues
L = np.diag(values)
# reconstruct the original matrix
B = Q.dot(L).dot(R)
print(B)# Code here [[1. 2. 3.]
[4. 5. 6.]
[7. 8. 9.]]
Above description provides an overview of eigendecomposition and covariance matrix. You are encouraged to visit following resources to get a deep dive into underlying mathematics for above equations.
The Eigen-Decomposition: Eigenvalues and Eigenvectors
Eigen Decomposition Visually Explained
## Summary
In this lesson, we looked at calculating covariance matrix for a given matrix. We also looked at Eigen decomposition and its implementation in python. We can now go ahead and use these skills to apply principle component analysis for a given multidimensional dataset using these skills.