This repository contains MATLAB code for estimating parameters for phase space reconstruction of multivariate data. The functions provided in this repository are described in the article:
Wallot & Mønster (2018) Calculation of average mutual information (AMI) and false-nearest neighbors (FNN) for the estimation of embedding parameters of multidimensional time-series in MATLAB Frontiers in Psychology, 9: 1679 DOI:10.3389/fpsyg.2018.01679
The functions in this repository can be used if you place the files containing them in a directory that is in your MATLAB Path. You can simply download mdDelay.m, autoMI.m and mdFnn.m or you can clone the whole repository to get all the files and examples:
git clone https://github.com/danm0nster/mdembedding.git mdembedding
If you want your cloned copy in a different directory you can change the last parameter to something else, e.g. mde-copy.
To embed time series data using the time-delayed embedding method two parameters are needed: the time delay and the embeddding dimension. We provide two functions to estimate these parameters: mdDelay() and mdFnn().
This is a short example of how to use the functions using the well-known Lorenz attractor. The data have been pre-generated and the MATLAB code for generating the plots can be found in this repository under docs/Lorenz, and you can also view the full output of the MATLAB notebook. Here, we will just show the basic commands used to produce plots and other outputs.
We start by loading the data generated by a numerical solution to the Lorenz equations
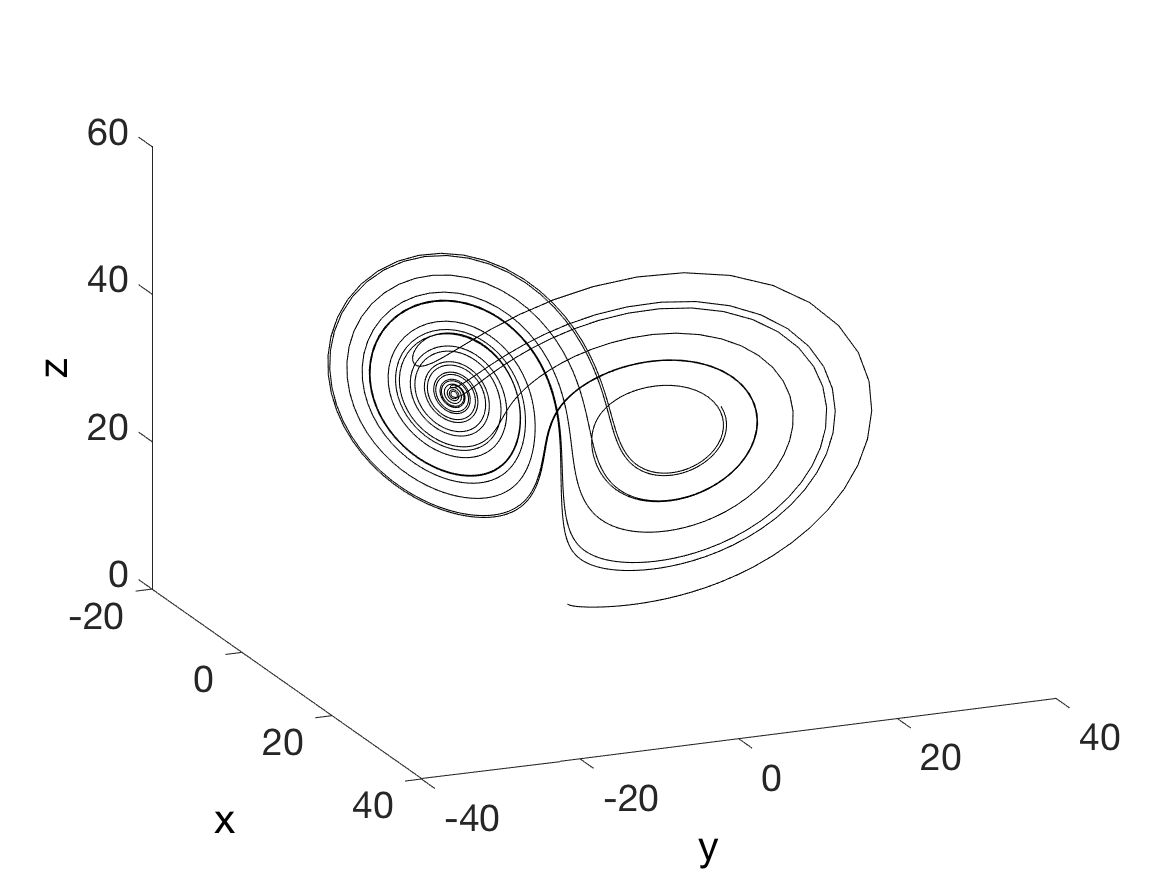
data = load('lorenz_3d_timeseries.txt');The data can be visualized by plotting the three variables x, y and z.
plot3(data(:,1), data(:,2), data(:,3), 'k')To estimate the proper time delay for embedding the data we use the function mdDelay.
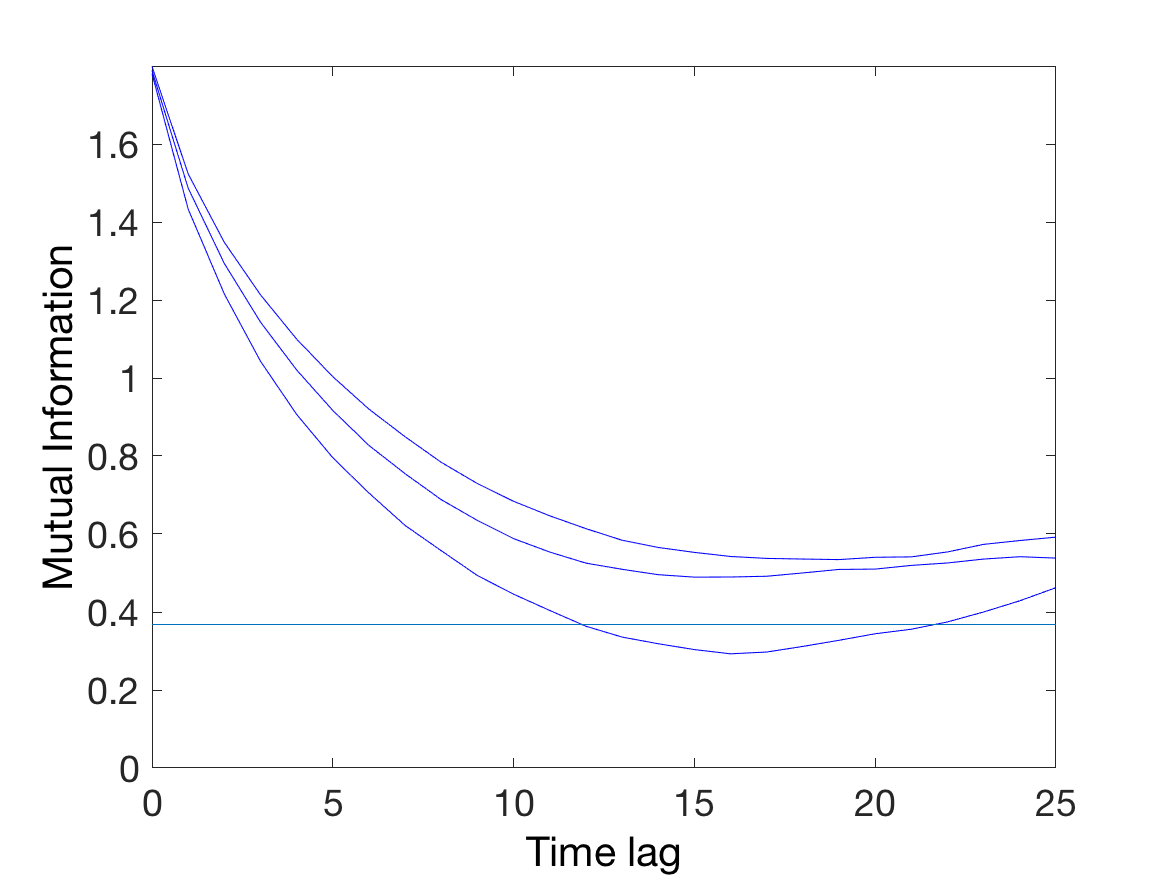
tau = mdDelay(data, 'maxLag', 25, 'plottype', 'all');This gives a value of tau that rounds to 15. A visual inspection of the plot of mutual information indicates that this is a reasonable value, since all three curves have minima close to that value. Alternatively we can get mdDelay() to plot the mean mutual information, by setting the plot type to "mean".
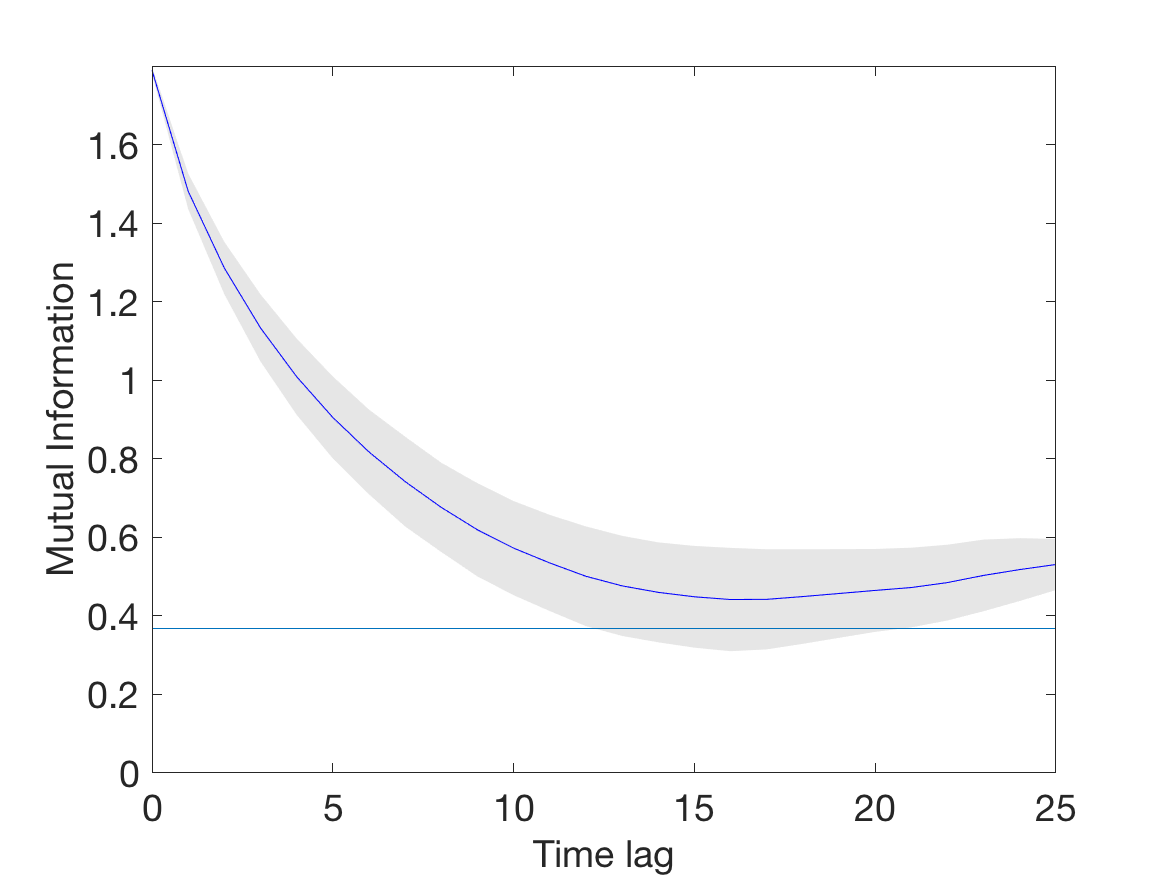
tau = mdDelay(data, 'maxLag', 25, 'plottype', 'mean');The optimal embedding dimension is estimated using the method of false nearest neighbors (FNN), which is implemented in the function mdFnn(). We call this function with the value of tau found above rounded to nearest integer (in this case 15). The function returns a vector with the percent of FNN and another vector with the corresponding embedding dimensions.
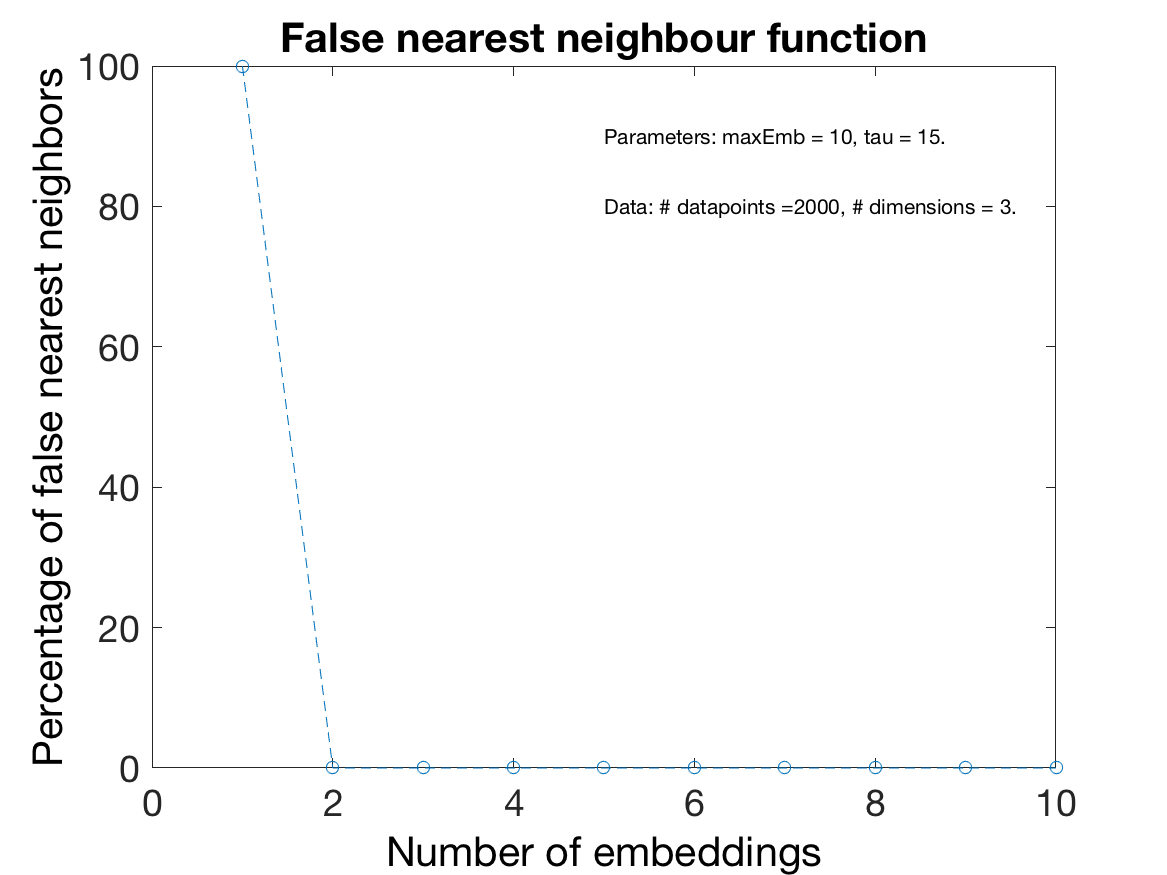
[fnnPercent, embeddingDimension] = mdFnn(data, round(tau));Since the number of false nearest neighbors drops to zero already at 2 embeddings we see that it is enough to embed the data in the three dimensions already present in the data, which is not surprising because we have sampled all the variables in the dynamical system.
You can run a short test suite for the functions by typing the following command in the MATLAB command window.
runtests('tests/mdDelayTest.m')If the test is successful you should see something like the output below.
Running mdDelayTest
No value below threshold found. Will use first local minimum instead
.No value below threshold found. Will use first local minimum instead
No value below threshold found. Will use first local minimum instead
.No value below threshold found. Will use first local minimum instead
No value below threshold found. Will use first local minimum instead
No value below threshold found. Will use first local minimum instead
No value below threshold found. Will use first local minimum instead
No value below threshold found. Will use first local minimum instead
.Teardown called. No action taken here.
Done mdDelayTest
__________
ans =
1×3 TestResult array with properties:
Name
Passed
Failed
Incomplete
Duration
Details
Totals:
3 Passed, 0 Failed, 0 Incomplete.
0.097622 seconds testing time.
If you find these functions useful and publish results where you have used them, please cite our paper:
Wallot & Mønster (2018) Calculation of average mutual information (AMI) and false-nearest neighbors (FNN) for the estimation of embedding parameters of multidimensional time-series in MATLAB Frontiers in Psychology, 9: 1679 DOI:10.3389/fpsyg.2018.01679