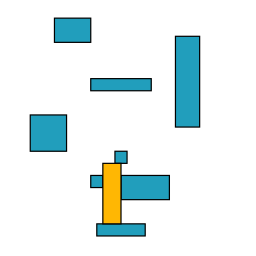This code generates generates all maximal empty rectangles (MERs) given a set of axis-aligned rectangular defects (or obstacles). A rectangle is empty if it does not contain any defect and is maximal if there is no other empty rectangle containing it. Perhaps more intuitively, a maximal empty rectangle is an empty rectangle that is delimited by defects.

For example, given the following defects:

we want to generate the following maximal empty rectangles:

Overview

The library can be installed directly from this repository using pip, as follows:

pip install git+https://git@github.com:danoneata/maximal-empty-rectangles.git

Here is how the maximal empty rectangles can be extracted:

from mer import get_maximal_empty_rectangles
board = Rectangle(left=0, top=0, right=2, bottom=2)
defects = [
    (0.45, 0.15, 0.30, 0.20),
    (0.75, 0.65, 0.50, 0.10),
    (1.45, 0.30, 0.20, 0.75),
    (0.25, 0.95, 0.30, 0.30),
    (0.95, 1.25, 0.10, 0.10),
    (0.75, 1.45, 0.10, 0.10),
    (1.00, 1.45, 0.40, 0.20),
    (0.80, 1.85, 0.40, 0.10),
]
defects = [Rectangle.from_corner_and_size(*d) for d in defects]
mers = get_maximal_empty_rectangles(board, defects)

Note that the get_maximal_empty_rectangles function assumes that the defects are placed in an enclosing rectangle (board), so it will generate additional MERs that are delimited by the defects and the board limits.

Explanation of the approach

Our approach is a sweep line algorithm and it was inspired by the following paper

Naamad, Amnon, D. T. Lee, and W-L. Hsu. "On the maximum empty rectangle problem." Discrete Applied Mathematics 8.3 (1984): 267-277. pdf

The main advantage of this implementation is that it scales quadratically in the number of defects, hence it is much more efficient than a naive approach. The naive approach has a complexity of O(n⁵), as it generates all possible rectangles (constructed from edges corresponding to any four defects) and picks only those that are maximal and empty. This latter method is implemented by the get_maximal_empty_rectangles_naive function and we use it primarily for testing (to ensure that the both approach yield the same set of MERs).

As an overview, the sweep line search starts from a given horizontal line corresponding to the bottom of a defect (and representing the top of a possible MER) and moves down, stopping at the top of all other defects (representing the bottom of a possible MER).

More precisely, the code consists of two nested loops. The first loop (outer loop) iterates through all defects' bottom lines (bot_line in code). These horizontal lines will represent the starting lines for the sweep line algorithm.

The code corresponding to this loop is:

list(concat(go(hline) for hline in bot_lines))

The second loop (inner loop) stops at the defects' top lines (top_lines in code).

The corresponding code is:

def go(hline: float) -> List[Rectangle]:
    state_init = State([], bot_to_defects[hline], P.closed(-P.inf, P.inf))
    state_final = reduce(iteration, top_lines, state_init)
    return state_final.candidates

The iteration step accumulates the information into a State data structure:

class State(NamedTuple):
    defects_top: List[Rectangle]
    candidates: List[Rectangle]
    limits_vertical: Any

The three fields of the State data structure are:

defects_top, which are the defects whose bottom line will determine the top of the candidates. These defects are fixed throughout the inner loop and are used in the process of refining the vertical limits of the candidates.
candidates, which are the maximal empty rectangles that are generated at each step. The candidates will be delimited horizontally by the top and bottom lines (top_line and bot_line), and vertically by the intervals in limits_vertical.
limits_vertical, which represent how much we can extend an MER from left to right. These limits are shortened as we encounter more defects.

Below we show a visual illustration of the iteration process for a given starting line. The initial point is the defect highlighted in dark blue, which will represent the top defect.

The gray area indicates the vertical limits (initially unconstrained) as well as the top horizontal limit (the bottom of the top defect).

We now sweep the line from top bottom (the inner loop), building candidates along the way. We take "snapshots" at the top of each defect, shown in light blue.

The first defect is above the top defect and outside the gray region; as such, it doesn't impact the state of the iteration.

The second defect is side-by-side with the top defect, and will limit the vertical limits of the candidates: as we cannot have an MER whose right margin goes beyond the light blue defect.

The third defect will limit the vertical limits by restricting the left margin of the potential candidates.

The next defect yields the first candidate and splits the regions of potential candidates into two:

The next line has two defects which will produce two candidates. Moreover, the defect on the right will block the vertical limits on the right.

Finally, the defect on the bottom will yield one more candidate:

As a final note, if we want to find the MERs within a rectangle, we can simply add the rectangle's borders as infinite rectangles:

defects_borders = [
    Rectangle(-P.inf, -P.inf, board.left, P.inf),
    Rectangle(-P.inf, -P.inf, P.inf, board.top),
    Rectangle(board.right, -P.inf, P.inf, P.inf),
    Rectangle(-P.inf, board.bottom, P.inf, P.inf),
]

Contributing

Testing:

pytest test