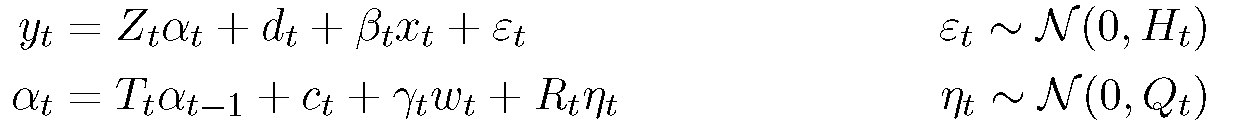MFSS - Mixed-Frequency State Space Modeling

Estimation and inference on state space models that allow for mixed-frequency time series data.

For an introduction to mixed-frequency state space modeling see "A Practitioner's Guide and Matlab Toolbox for Mixed Frequency State Space Models" by Scott Brave, Andrew Butters, and David Kelley.

Installation

The easiest way to use MFSS is to install it via the toolbox (MFSS.mltbx) by dragging it into the Matlab command window. It should install as an Add-On and be available on your path whenever using Matlab.

MFSS requires the following Matlab toolboxes:

Optimization Toolbox
Statistics and Machine Learning Toolbox

Further functionality is available through the use of additional toolboxes:

Global Optimization Toolbox
Symbolic Math Toolbox
Parallel Computing Toolbox

Some examples and tests additionally use the Econometrics Toolbox.

Compatibility

MFSS has been tested on Matlab 2017b-2018b.

It is incompatible with Octave (through at least 4.4.1).

Getting Started

State space models take the form

For more information on how to put models into this form, see the examples in /examples.

Mixed-frequency data

To handle mixed-frequency data, first set up the model (see below) as if the data were all observed at the highest (base) frequency. Then, create an Accumulator to augment the system to make sure it obeys the temporal properties of the data. Two methods of creating an Accumulator exist.

For regularly spaced data (where the number of high-frequency periods in each low-frequency period is fixed for each series), the properties of the timing can be inferred from the data itself. Provide the type (sum or average) and period for each series:

accum = Accumulator.GenerateRegular(y, {'sum', 'avg', 'avg', ''}, [3 1 3 0]);

For series with irregularly spaced observations (for example, monthly data observed from a weekly model), the calendar and horizon of the accumulator must be specified explicitly:

accum = Accumulator(accumulatorIndexes, calendar, horizon);

With the accumulators defined, we can "augment" a StateSpace or StateSpaceEstimation to ensure it obeys the timing we observe:

ssA = accum.augmentStateSpace(ss);
ssEA = accum.augmentStateSpaceEstimation(ssE);

For more information on how to specify and use accumulators, see the User Guide.

Working with known parameters

With the matrices Z, d, β, H, T, c, γ, R, Q known, we can create a StateSpace object:

ss = StateSpace(Z, H, T, Q);
ss = StateSpace(Z, H, T, Q, 'd', d, 'beta', beta, 'c', c, 'gamma', gamma, R', R);

With a StateSpace object, we can get the filtered or smoothed estimates of the latent state:

a = ss.filter(y);
a = ss.filter(y, x, w);
alpha = ss.smooth(y);
alpha = ss.smooth(y, x, w);

We can also get the decomposition of the smoothed or filtered estimates according to the source of the inference on the state:

[yContribution, parameterContribution] = ss.decomposed_smoothed(y);
[yContribution, parameterContribution, xContribution, wContribution] = ss.decomposed_smoothed(y, x, w);

Estimating Parameters

To estimate parameters, set elements of the system matrices to nan or symbolic variables, then create a StateSpaceEstimation:

ssE = StateSpaceEstimation(Z, H, T, Q);
ssE = StateSpaceEstimation(Z, H, T, Q, 'd', d, 'beta', beta, 'c', c, 'gamma', gamma, R', R);

Before estimating, set parameters for estimation including choice of optimization, tolerance, and parallel computing preferences (among others):

ssE.solver = 'sa'; % Simulated annealing
ssE.solveTol = 1e-6;
ssE.parallel = true;

With the estimation set up, create a StateSpace by estimating the unknown parameters:

ss = ssE.estimate(y);
ss = ssE.estimate(y, x, w);

VAR Estimation

Since vector autoregressions tend to have many more parameters than other models, an expectation-maximization (EM) algorithm is available for estimation. To create a model object, specify the data, the number of lags, and the accumulator, then estimate it on the data:

varMdl = MFVAR(y, 2, accum);
ssEstimated = varMdl.estimate();

Building the mex files

Substantial performance improvements are possible through using compiled versions of the Kalman filter/smoother functions.

To build, a mex C/C++ compiler is required. The required library (Armadillo) is included in the mex directory. A complete build of the mex files should be done by running mex/make.m.

Before running make.m, set up the mex compiler by following the instructions here.

Building the Toolbox

To build the toolbox (MFSS.mltbx), run build/make_toolbox.m. This process is sensitive to the paths available when running this file since they will be included when creating the package. Refer to make_toolbox.m for more instructions on how to build the toolbox.

Using the make_toolbox.m script will update the minor version number of the toolbox. It will produce a toolbox file which can be installed in other copies of Matlab by dragging it to the command window.

When updating the installed version of the toolbox, previous versions should be uninstalled first through the Matlab Add-On Manager to avoid name conflicts.

Credits

This library uses Armadillo.

If you use this toolbox in preparing a publication, please cite

Scott A. Brave, R. Andrew Butters, David Kelley (2022). A Practitioner's Guide and MATLAB Toolbox for Mixed Frequency State Space Models, Journal of Statistical Software, 104(10). doi:10.18637/jss.v104.i10

For details on any references in the code, see this publication.

davidakelley/MFSS