An algorithm for calculating the phase of the moon between 1970 and 2149 is presented below.
This algorithm actually calculates the fraction of the moon's disk that is illuminated by the sun as seen from the earth. This is equal to the fraction of the moon's diameter illuminated by the sun along every chord perpendicular to the axis of the phase.
#include <math.h>
/**
* @arg sec the number of seconds since 1970 Jan 1 00:00:00 UTC
* @arg is_waxing if not null, then will contain true if the moon
* is waxing
* @return the illuminated fraction of the moon's disk as seen from earth,
* accurate to 0.3% during the entire period 1970 - 2149
*
* @author github.com/deirdreobyrne
*/
double getPhase(double sec, int *is_waxing) {
double d = fmod(4.847408287988257 + sec/406074.7465115577, 2.0*M_PI);
double m = fmod(6.245333801867877 + sec/5022682.784840698, 2.0*M_PI);
double l = fmod(4.456038755040014 + sec/378902.2499653011, 2.0*M_PI);
double i = fmod(d
+1.089809730923715e-01 * sin(l)
-3.614132757006379e-02 * sin(m)
+2.228248661252023e-02 * sin(2.0*d-l)
+1.353592753655652e-02 * sin(2.0*d)
+4.238560208195022e-03 * sin(2.0*l)
+1.961408105275610e-03 * sin(d)
,2.0*M_PI);
if (is_waxing) {
*is_waxing = (i <= M_PI);
}
return (1.0 - cos(i))/2.0;
}The argument is the number of seconds since 1970 Jan 1 00:00:00 UTC. The return result is the fraction of the moon's disk illuminated by the sun as seen from the earth. The accuracy is to within 0.003 during the entire period 1970-2149.
If you cut off some of the terms in the equation for double i in getPhase(...) you can increase the speed and reduce the footprint of the algorithm in a trade-off with accuracy. This could be useful, for instance, in a smartwatch which has only a small screen anyway in which to display the moon's phase, and which has limited resources which need to be managed.
This table gives the maximum error in the period 1970 - 2149 when some terms are omitted.
| Omit starting from | Accuracy |
|---|---|
| ... sin(l) | 0.085961 |
| ... sin(m) | 0.036612 |
| ... sin(2.0*d-l) | 0.020229 |
| ... sin(2.0*d) | 0.010333 |
| ... sin(2.0*l) | 0.004811 |
| ... sin(d) | 0.003269 |
| nothing | 0.002875 |
In other words, if an accuracy of 9% is sufficient for your application, you can use double i = fmod(d, 2*M_PI); and get rid of the calculations for double m = ... and double l = ....
The formula presented is of the same form as given in Jean Meeus' excellent 1991 book Astronomical Algorithms page 346. Meeus' formula is truncated, and has a maximum error of 0.003443 in the period 1970 - 2149.
Astronomical predictions can only be made in a timescale that is uniform. In most cases, that means a timescale known as "TDT". Civil time is based on a different timescale, called "UTC", which is kept to within 0.9 seconds of yet another timescale called "UT1". UT1 keeps track of the Earth's rotation so that it is generally around noon when the sun is at its highest in Greenwich. But the Earth's rotation is not uniform - things like earthquakes affect it. So, the difference between the TDT and UT1 (imaginatively called ΔT) is not constant and not predictable. I adopted a very simple and reasonably accurate formula (for historical times, anyway) for ΔT —
where d is the number of days elapsed since 1970 Jan 1 00:00:00 UTC.
My first step was to get a dataset. I decided on the period from 1970 Jan 1 00:00:00 using a step size of 3 hours for 219 steps (524,288 steps), making 2149 Jun 6 21:00:00 the last entry in the dataset.
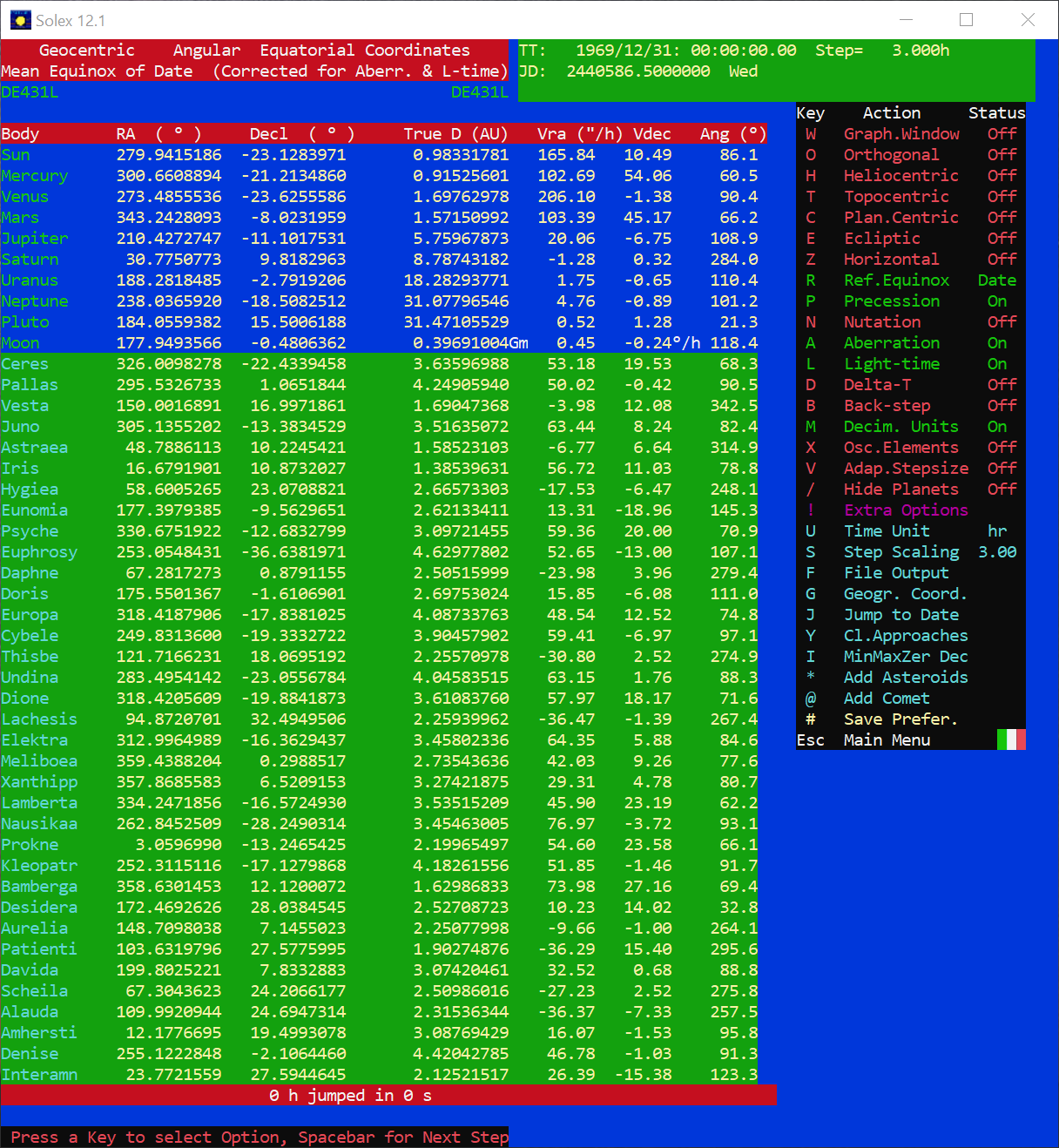
My first step was to get a dataset of phases of the moon. To that end, I used the excellent Solex program using the settings below
I ran for 525,000 steps, so that I would cover the period of interest, and created SUN.OUT and MOON.OUT files. After some vim magic, I was left with two csv files - one for the sun and another for the moon - containing the julian date, the right ascension, declination, and distance.
Using GNU Octave, I passed those csv files through octave/create_phase_csv.m to create phase.csv
After much trial and error, it was discovered that the best method of quickly calculating the moon's phase to good accuracy was to use ecliptic coordinates, and to ignore the ecliptic latitude of both the sun and the moon. Hence I switched Solex over to Ecliptic coordinates and performed another run.
This time I passed the SUN.OUT and MOON.OUT files through a simple Perl script to generate dlambda.csv - a csv file containing the difference in ecliptic longitudes of the moon and sun.
A quick check shows that using this simplified method of calculating the phase of the moon has a maximum error potential of about 0.2%. However, I suspect including a sin(D) term in the final formula helps with accuracy, as it would be the first-order term in a correction for the parallax of the moon's orbit as seen from the sun.
Creating the formula involved a few steps of using FFTs to find which terms should be included. In the end, however, I used the form in Jean Meeus' excellent 1991 book Astronomical Algorithms page 346.
The final Octave fitting script is below -
pkg load optim;
format long;
data = csvread("phase.csv");
n=524288;
t = data([1:n],1);
phase = data([1:n],2);
args = [
4.060747465115577e+05
4.847408287988257e+00
5.022682784840698e+06
6.245333801867877e+00
3.789022499653011e+05
4.456038755040014e+00
1.089809730923715e-01
-3.614132757006379e-02
2.228248661252023e-02
1.353592753655652e-02
1.961408105275610e-03
4.238560208195022e-03
];
dargs = [
1e-6
1e-3
1e-6
1e-3
1e-6
1e-3
1e-3
1e-3
1e-3
1e-3
1e-3
1e-3
];
D = @(t,p) polyval([1/p(1),p(2)],t);
M = @(t,p) polyval([1/p(3),p(4)],t);
L = @(t,p) polyval([1/p(5),p(6)],t);
func = @(t,p) (1-cos(D(t,p) + p(7)*sin(L(t,p)) + p(8)*sin(M(t,p)) ...
+ p(9)*sin(2*D(t,p)-L(t,p)) + p(10)*sin(2*D(t,p)) ...
+ p(11)*sin(D(t,p)) + p(12)*sin(2*L(t,p))))/2;
max(abs(phase-func(t,args)))
[myphase,newargs,cvg,iter]=leasqr(t, phase, args, func, 0.0000001, 20, ones(size(t)), dargs);
cvg
iter
newargs - args
newargs
max(abs(phase-myphase))