mglasso: An R repository from desanou

Method

This repository provides an implementation of the MGLasso (Multiscale Graphical Lasso) algorithm: an approach for estimating sparse Gaussian Graphical Models with the addition of a group-fused Lasso penalty.

MGLasso is described in the paper Inference of Multiscale Gaussian Graphical Model. MGLasso has these contributions:

We simultaneously infer a network and estimate a clustering structure by combining the neighborhood selection approach (Meinshausen and Bühlman, 2006) and convex clustering (Hocking et al. 2011).
We use a continuation with Nesterov smoothing in a shrinkage-thresholding algorithm (CONESTA, Hadj-Selem et al. 2018) to solve the optimization problem.

To solve the MGLasso problem, we seek the regression vectors $\beta^i$ that minimize

$J_{\lambda_1, \lambda_2}(\boldsymbol{\beta}; \mathbf{X} ) = \frac{1}{2} \sum_{i=1}^p \left \lVert \mathbf{X}^i - \mathbf{X}^{\setminus i} \boldsymbol{\beta}^i \right \rVert_2 ^2 + \lambda_1 \sum_{i = 1}^p \left \lVert \boldsymbol{\beta}^i \right \rVert_1 + \lambda_2 \sum_{i < j} \left \lVert \boldsymbol{\beta}^i - \tau_{ij}(\boldsymbol{\beta}^j) \right \rVert_2.$

MGLasso package is based on the python implementation of the solver CONESTA available in pylearn-parsimony library.

Package requirements and installation

Install the reticulate package and Miniconda if no conda distribution available on the OS.

install.packages('reticulate')
reticulate::install_miniconda()

Install MGLasso, its python dependencies and configure the conda environment rmglasso.

# install.packages('mglasso')
remotes::install_github("desanou/mglasso")

library(mglasso)
install_pylearn_parsimony(envname = "rmglasso", method = "conda")
#> + "C:/Users/doedm/AppData/Local/r-miniconda/condabin/conda.bat" "install" "--yes" "--name" "rmglasso" "python=3.8"
reticulate::use_condaenv("rmglasso", required = TRUE)
reticulate::py_config()
#> python:         C:/Users/doedm/AppData/Local/r-miniconda/envs/rmglasso/python.exe
#> libpython:      C:/Users/doedm/AppData/Local/r-miniconda/envs/rmglasso/python38.dll
#> pythonhome:     C:/Users/doedm/AppData/Local/r-miniconda/envs/rmglasso
#> version:        3.8.13 (default, Mar 28 2022, 06:59:08) [MSC v.1916 64 bit (AMD64)]
#> Architecture:   64bit
#> numpy:          C:/Users/doedm/AppData/Local/r-miniconda/envs/rmglasso/Lib/site-packages/numpy
#> numpy_version:  1.22.4
#> conesta_solver: [NOT FOUND]
#> 
#> NOTE: Python version was forced by use_python function

The conesta_solver is delay loaded. See reticulate::import_from_path for details.

An example of use is given below.

Illustration on a simple model

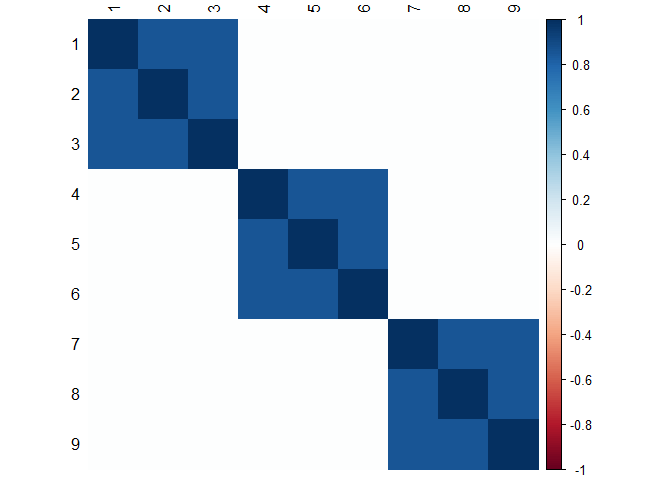
Simulate a block diagonal model

We simulate a -block diagonal model where each block contains variables. The intra-block correlation level is set to while the correlations outside the blocks are kept to .

library(Matrix)
n = 50
K = 3
p = 9
rho = 0.85
blocs <- list()

for (j in 1:K) {
  bloc <- matrix(rho, nrow = p/K, ncol = p/K)
  for(i in 1:(p/K)) { bloc[i,i] <- 1 }
  blocs[[j]] <- bloc
}

mat.correlation <- Matrix::bdiag(blocs)
corrplot::corrplot(as.matrix(mat.correlation), method = "color", tl.col="black")

Simulate gaussian data from the covariance matrix

set.seed(11)
X <- mvtnorm::rmvnorm(n, mean = rep(0,p), sigma = as.matrix(mat.correlation))
colnames(X) <- LETTERS[1:9]

Run `mglasso()`

We set the sparsity level $\lambda_1$ to and rescaled it with the size of the sample.

X <- scale(X)    
res <- mglasso(X, lambda1 = 0.2*n, lambda2_start = 0.1, fuse_thresh = 1e-3, verbose = FALSE)

To launch a unique run of the objective function call the conesta function.

temp <- mglasso::conesta(X, lam1 = 0.2*n, lam2 = 0.1)

Estimated clustering path

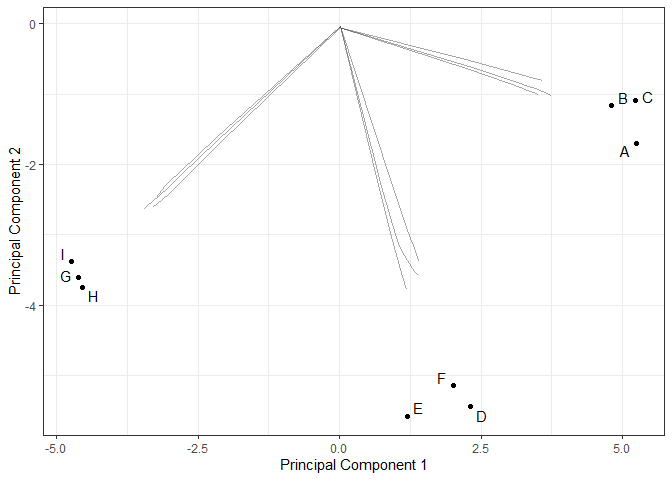
We plot the clustering path of mglasso method on the 2 principal components axis of . The path is drawn on the predicted ’s.

library(ggplot2)
library(ggrepel)
mglasso:::plot_clusterpath(as.matrix(X), res)

Estimated adjacency matrices along the clustering path

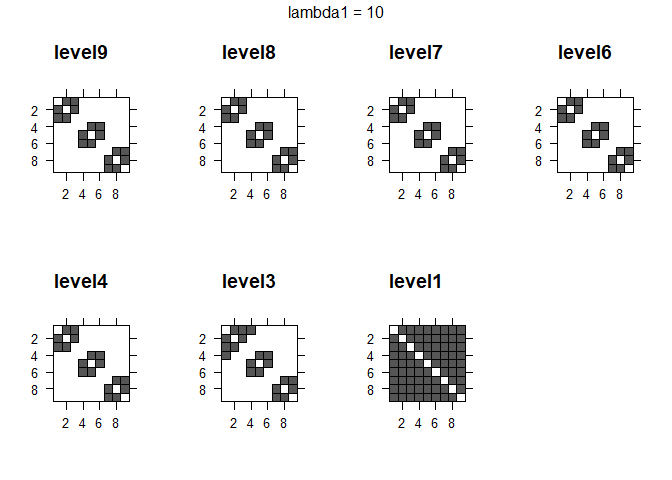
As the the fusion penalty increases from level9 to level1 we observe a progressive fusion of adjacent edges.

plot_mglasso(res)

Reference

Edmond, Sanou; Christophe, Ambroise; Geneviève, Robin; (2022): Inference of Multiscale Gaussian Graphical Model. ArXiv. Preprint. https://doi.org/10.48550/arXiv.2202.05775

desanou/mglasso