dfleta/probabilidad-bayes-MIA

Recursos sobre manejo de la incertidumbre y probabilidad por un agente inteligente, módulo de Modelos de Inteligencia Artificial

RED DE BAYES

Código del curso CS50’s Introduction to Artificial Intelligence with Python, lecture 2 "uncertainty", refactorizado a la nueva api de pomegranate v1.0.4 por jmschrei

Instalación

Es necesario el uso del paquete Pomegranate:

Pomegranate is a python package which implements fast, efficient, and extremely flexible probabilistic models ranging from probability distributions to Bayesian networks to mixtures of hidden Markov models.

python -m venv venv

source venv/bin/activate

Instalar la versión estricta de pomegranate v1.0.4:

pip install -r requirements.txt

o

pip install pomegranate

Uso

Red de Bayes

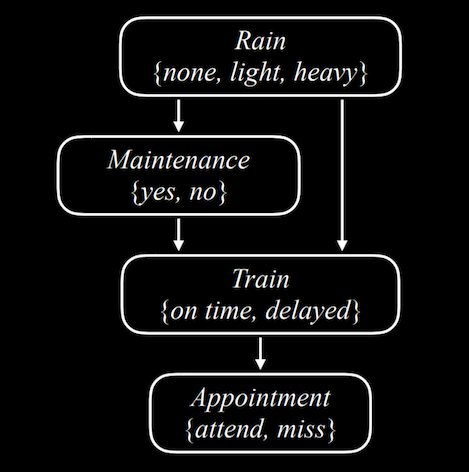
El código codifica la siguiente red de Bayes, en el módulo model.py:

Rain es el nodo raíz de la red. Rain es una variable aleatoria que toma los valores en el dominio atómico {none, light, heavy}. Su distribución de probabilidad es:

none	light	heavy
0.7	0.2	0.1

Maintenance indica si se realiza mantenimiento en la red de transporte, tomando los valores atómicos {yes, no}. Rain es el nodo padre de Maintenance, lo que significa que su distribución de probabilidad se ve afectada por por Rain.

R	yes	no
none	0.4	0.6
light	0.2	0.8
heavy	0.1	0.9

Train es la variable que codifica si el tren llega {on time, delayed}. Maintenance y Rain son padres de Train, que implica que su distribución de probabilidad está condicionada por la de sus nodos padre:

$$ P(X | Padres(X)) $$

R	M	on time	delayed
none	yes	0.8	0.2
none	no	0.9	0.1
light	yes	0.6	0.4
light	no	0.7	0.3
heavy	yes	0.4	0.6
heavy	no	0.5	0.5

Appointment toma los valores {attend, miss}. Es el único nodo padre de Train, indicando que lo que en última instancia afecta a llegar a tiempo a la cita es que el tren llegue puntual o no. Si el tren llega puntual, que llueva de manera torrencial o sea orballo no tiene efecto en llegar a tiempo a la cita.

T	attend	miss
on time	0.9	0.1
delayed	0.6	0.4

Probabilidad conjunta

Calculamos la probabilidad de un determinado evento dada una observación, una observación de todas las variables, por lo que hablamos de probabilidad conjunta o joint probabililty.

¿Cual es la probabilidad de que no llueva, no se realice mantenimiento, el tren llegue puntual y asistamos a la cita?

$$ P(light)P(no | light)P(on time | light, no)P(attend | on time) $$

$$ P(light, no, on time, attend) $$

$ python likelihood.py

tensor([0.3402])

Inferencia por enumeración

¿Cuáles son las distribuciones de probabilidades para todas las variables dada una evidencia, una observación?

Dada una observación o evidencia $e$, aplicamos la inferencia por enumeración iterando sobre las probabilidades de las variables ocultas $y$ :

$$ P(X|e) = \frac{P(X,e)}{P(e)} = \alpha P(X,e) = \alpha \sum_{y} {P(X,e,y)} $$

Con la observación de que el tren se ha retrasado, calculamos las distribuciones de probabilidad de las variables Rain, Maintenance y Appointment.

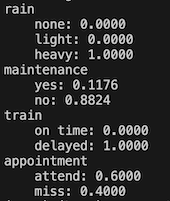
$ python inference.py

rain
    none: 0.4583
    light: 0.3069
    heavy: 0.2348
maintenance
    yes: 0.3567
    no: 0.6433
train
    on time: 0.0000
    delayed: 1.0000
appointment
    attend: 0.6000
    miss: 0.4000

likelihood.py y inference.py son dependientes del módulo model.py.

En el código de estos tres ficheros encontrarás la explicación de cómo se codifica la red de bayes en pomegranate.

Ejercicio inferencia

Intenta calcular la probabilidad de llegar a tiempo o tarde a la cita, dependiendo de que el tren llegue tarde (delayed) y se produzca lluvia fuerte (heavy).

¿Ha cambiado la probabilidad de atender a la cita respecto al ejemplo anterior? ¿Por qué?

Chequea la configuración en el fichero inference_ejercicio.py.

Rejection sampling

Como la inferencia por enumeración puede resultar computacionalmente ineficiente, es posible implementar el cálculo de la distribución de la probabilidad de la variable appoinment (perder la cita, miss o attend) en función de la probabilidad condicionada a que el tren llegue tarde (delayed), mediante el método rejection sampling.

$$ P(Appoinment| Train = delayed) = \frac{P(Appoinment, Train = delayed)}{P(Train = delayed)} = \ = \alpha P(Appoinment, Train = delayed) = \ = \alpha \sum_{y \in Rain, Maintenance } {P(Appoinment, Train = delayed,y)} $$

Se trata de tomar N muestras sobre la red de bayes y seleccionar aquellas que verifiquen que:

[?, ?, 1, 0]  [rain, maintenance, "delayed", "attend"]
[?, ?, 1, 1]  [rain, maintenance, "delayed", "miss"]

Si el caso fuese Rain = light y Train = ontime, el muestreo correspondería a la figura:

Rejection samplig un cálculo aproximado de la probabilidad, que variará en función del número de muestras sampleadas que categoricemos como attend o miss, por lo que la ejecución de sample.py arroja ligeras variaciones en el conteo de cada muestra.

Consulta el módulo sammple.py.

$ python sample.py

Counter({'attend': 1224, 'miss': 884})
# y en sucesivos muestreos
Counter({'attend': 1216, 'miss': 821})
Counter({'attend': 1231, 'miss': 843})
Counter({'attend': 1340, 'miss': 826})

¿Cuál es la distribución de probabilidad normalizada? Para el último muestreo:

$$ P(Appoinment| Train = delayed) = < 0.616, 0.384> $$

Likelihood weighting

En el ejemplo anterior se observa que en 10K muestras se rechazan aproximadamente el 80% de las muestras sampleadas. Esto es otro motivo de ineficiencia computacional.

Podemos realizar el muestreo esta ve fijando el valor de las variables observadas, las evidencias, y no muestrelarlas. Calcularemos las probabilidades condicionales del resto de variables usando la red de Bayes o de creencia, y multiplicaremos cada muestra por su probabilidad.

Recursos sobre probabilidad y redes de Bayes

Mi compañero @alejandro del curso de especialización en IA y Big Data del IES de Teis en la modalidad a distancia ha preparado estos recursos en castellano: Matemáticas para Machine Learning.

Recordad que esta práctica intenta cubrir los contenidos de los capítulos 12 Quantifying Uncertainty y 13 Probabilistic Reasoning del libro IA, un enfoque moderno de Russell & Norvig. Allí encontraréis explicacos en profundidad los conceptos más importantes sobre teoría de probabilidad que explicamos de manera práctica en clase sobre estos dos supuestos prácticos:

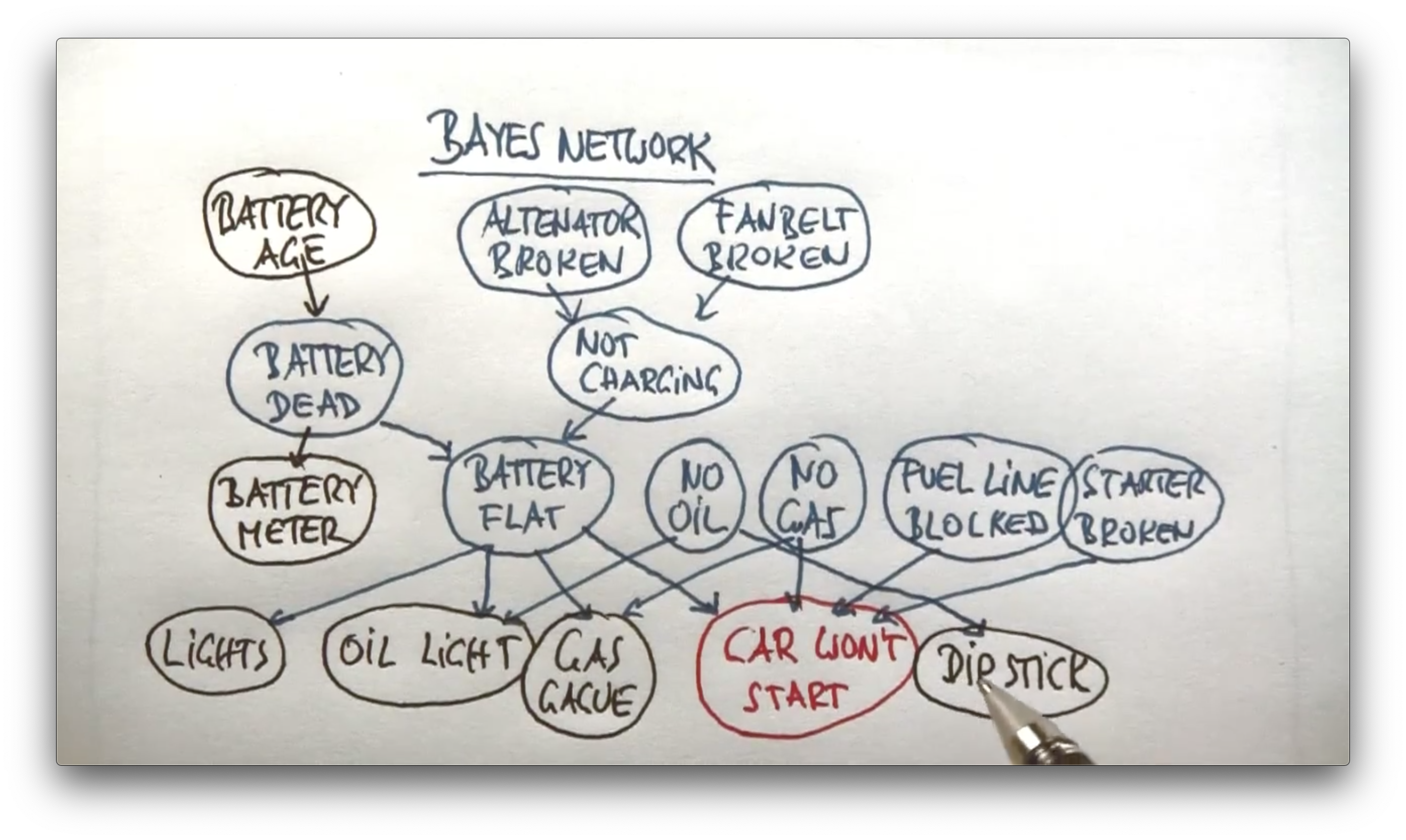
• "Trata de arrancarlo" o "Un sistema de diagnóstico de averías inteligente como asistente para mecánicos", un ejemplo explicado por Sebastian Thrun en su famoso y pionero MOCC sobre IA:

• Probabilidades sobre dos dados:

Principios

Los principios más importantes para comprender la teoría de probabilidades son:

• La letra griega $\Omega$ (omega mayúscula) representa el espacio de muestras, y $\omega$ (omega minúscula) se refiere a los elementos de ese espacio, es decir, a los posibles mundos.

• Los posibles mundos son mútuamente exclusivos y exhaustivos: dos posibles mundos no pueden existir a la vez, y uno de los posibles mundos debe producirse.

• Un modelo de probabilidad completamente especificado asocia una probabilidad numérica $P(ω)$ con cada posible mundo.

• El axioma básico de la teoría de la probabilidad enuncia que todo mundo posible tiene una probabilidad entre 0 y 1, y que la probabilidad total del conjunto de posibles mundos es es 1:

$$ 0 \leq P(ω) \leq 1 \quad \forall \omega $$

$$ \sum_{w\in\Omega} P(ω)=1 $$

Ejemplo

Jugamos con tres cartas, una reina $Q$, un rey $K$ y un comodín (o jack) $J$. Todas las cartas están boca abajo, elegimos una al azar y le damos la vuelta. ¿Cuál es el conjunto de resultados? Los posibles resultados son $\Omega = { Q, K, J}$

Negación

$$ P(A) = 1 - P(\neg A) $$

si $A$ y $A^c$ son disjuntos.

$$ P(A^c \cup A) = P(A^c) + P(A) = P(\Omega) = 1 $$

Independencia

Dos eventos $A$ y $B$ son independientes si y sólo si:

$$ P(A \cap B) = P(A)P(B) $$

Ejemplo

El espacio de muestras de un dado de seis caras es $\Omega = { 1, 2, 3, 4, 5, 6 }$

En un dado sin trucar, cada muestra tiene la misma probabilidad $P(\omega) = 1/6$. Si lanzamos dos dados, el resultado de cada dado es independiente del otro. ¿Cuál es la probabilidad de obtener dos treses?

$$ P(tres \cap tres) = P(tres)P(tres) = (1/6) \times (1/6) = 1/36 $$

Este ejemplo también sirve para demostrar que dos sucesos son independientes. Dos sucesos son independientes si $P(A \cap B) = P(A)P(B)$.

La probabilidad de obtener un tres en uno de los dados es $1/6$, igual que la probabilidad de obtener $1/6$ en el otro dado. Por tanto: $P(A)P(B)= (1/6) \times (1/6) = 1/36$

La probabilidad de obtener dos treses se puede calcular dividiendo el número de las muestras que satisfacen esa condición entre el número total de muestras:

$$ P(A \cap B) = \frac {Número \ de \ muestras \ en \ A \cap B}{Número \ total \ de \ muestras \ en \ \Omega } $$

El número total de muestras en $\Omega$ es $36$ (son las posibles combinaciones de los 6 valores de cada uno de los dos dados). El número de muestras con dos $treses$ es $1$. Por tanto $P(F) = 1/36$. Se verifica, por tanto, que los sucesos son independientes porque $P(A)P(B)= 1/36 = P(A \cap B)$.

Marginalización

$$ P(A) = P(A,B) + P(A, \neg B) $$

también expresada para variables aleatorias como:

$$ P(X=x_i) = \sum_j(X=x_i, Y=y_j) $$

Teorema de la Probabilidad Total

$$ P(A) = P(A|B) P(B) + P(A|\neg B) P(\neg B) $$

$$ P(A) = \sum_i P(A|B_i) P(B_i)$$

Inclusión - Exclusión

$$ P(A \vee B) = P(A) + P(B) - P(A \wedge B)$$