Tensor Core 是 NVIDIA 推出的一种 GPU 架构,它专门用于计算矩阵运算。Tensor Core 可以提供高效的半精度运算,这在深度学习和 AI 领域非常有用。Tensor Core 可以实现矩阵乘法和矩阵加法,这些运算在深度学习中非常常见。
Tensor Core 可以大幅提高深度学习模型的训练速度和推理速度。它可以支持各种类型的网络,包括 CNN,RNN 和 GAN。Tensor Core 还可以用于其他类型的矩阵运算,例如线性代数和信号处理。
Tensor Core 的架构包括专门的矩阵乘法单元 (MMA) 和矩阵加法单元 (MMA)。这些单元可以在半精度浮点数 (FP16) 上运行,这使得它们能够在精度和性能之间取得平衡。
在性能方面,Tensor Core 可以提供高达 12 个 TFLOPS 的矩阵乘法性能和 24 个 TFLOPS 的矩阵加法性能。这使得它能够大幅加速深度学习模型的训练和推理。
Tensor Core 还支持其他类型的矩阵运算,例如矩阵转置,矩阵乘法和矩阵加法。这使得它可以用于各种类型的应用,包括深度学习,线性代数和信号处理。
在深度学习中,Tensor Core 用来加速训练和推理过程。
- 在训练中,Tensor Core 可以帮助更快地进行大量矩阵运算,如卷积运算和矩阵乘法,从而加快模型的训练速度。
- 在推理中,Tensor Core 可以帮助更快地进行大量矩阵运算,并且可以在线性时间内完成运算,这使得实时性能更高,更适合实时应用。
- Tensor Core 也支持更高的精度,比如 FP16 和 bfloat16,这使得训练更稳定,模型的性能也更好。
与 GPU 或 CPU 相比,Tensor Core 在矩阵运算性能上有明显优势。
- 与 GPU 相比,Tensor Core 可以在同样的时间内处理更多的矩阵运算,并且支持更高的精度,这使得它在深度学习中的性能表现更佳。
- 与 CPU 相比,Tensor Core 在矩阵运算性能上有更高的并行性和更快的速度,这使得它在训练和推理大规模深度学习模型时更加高效。
- 但是 Tensor Core 主要是用于矩阵运算,对于其他运算,性能可能不如其他 GPU 或 CPU。
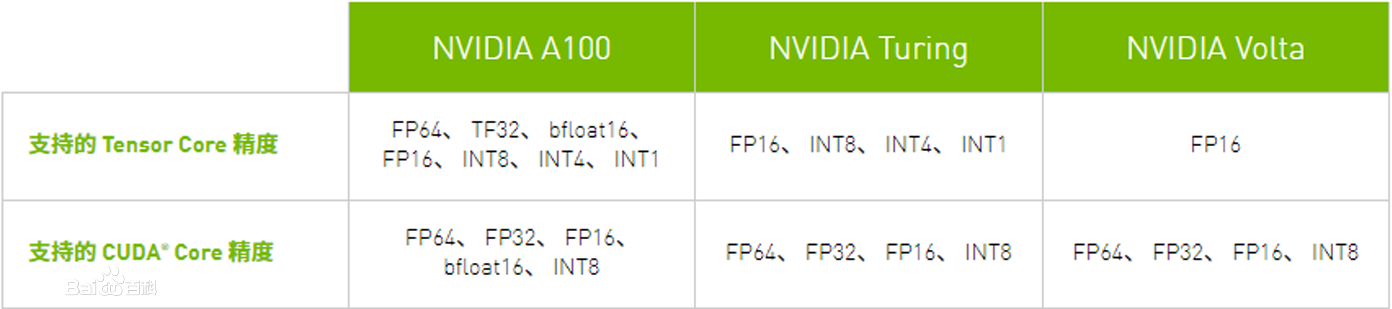
- 第一代 Tensor Core :NVIDIA Volta 架构: 通过 FP16 和 FP32 下的混合精度矩阵乘法提供了突破性的性能;
- 第二代 Tensor Core :NVIDIA Turing 架构: Turing Tensor Core 提供了一系列用于深度学习训练和推理的精度(从 FP32 到 FP16 再到 INT8 和 INT4),Turing 架构也在消费级 GeForce 产品线上配备 Tensor Core ,另 GeForce RTX 20 系列显卡具备了全新的 AI 硬件加速计算能力;
- 第三代 Tensor Core :NVIDIA Ampere 架构: 可覆盖研究人员需要的全系列精度(TF32、FP64、FP16、INT8 和 INT4),从而加速和简化 AI 的采用,并将 NVIDIA Tensor Core 的强大功能扩展到 HPC 领域。
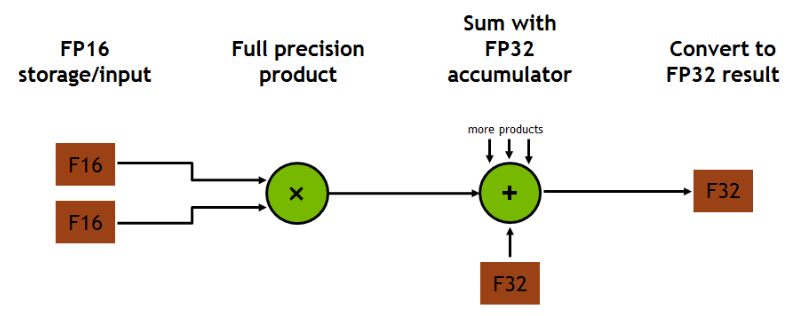
每个 Tensor Core 提供一个 4x4x4 矩阵处理阵列,执行操作 D=A*B+C,其中 A、B、C 和 D 是 4×4 矩阵,如下图所示。矩阵乘法输入 A 和 B 是 FP16 矩阵,而累加矩阵 C 和 D 可以是 FP16 或 FP32 矩阵。
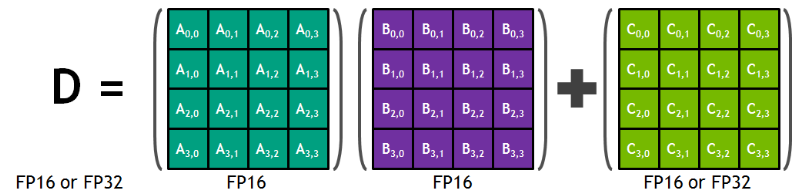
每个 Tensor Core 每个时钟周期执行 64 个浮点 FMA 混合精度操作(FP16 输入乘以全精度乘积,FP32 累加)。 SM(流处理器)中的 8 个 Tensor 核心每个时钟周期总共执行 1024 个浮点操作。
如下图所示,对于 4x4x4 矩阵乘法,FP16 乘法产生全精度结果,该结果在 FP32 运算中与给定点积中的其他乘积累加。
本文采用 Baidu, NVIDIA, Intel, ARM, AMD 联合开发的 DeepBench 进行测试。以 TFLOPS (每秒浮点运算次数) 大小作为评价指标。
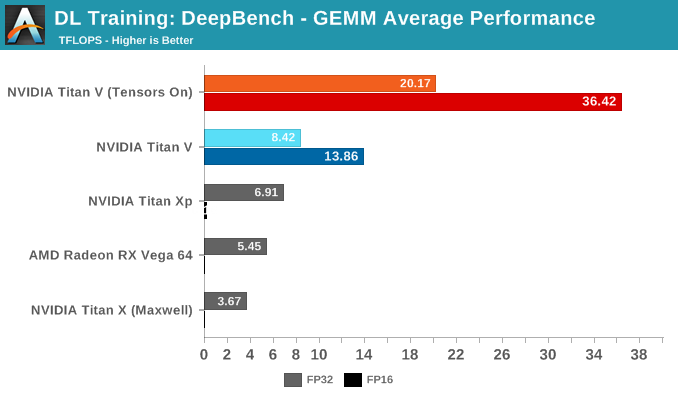
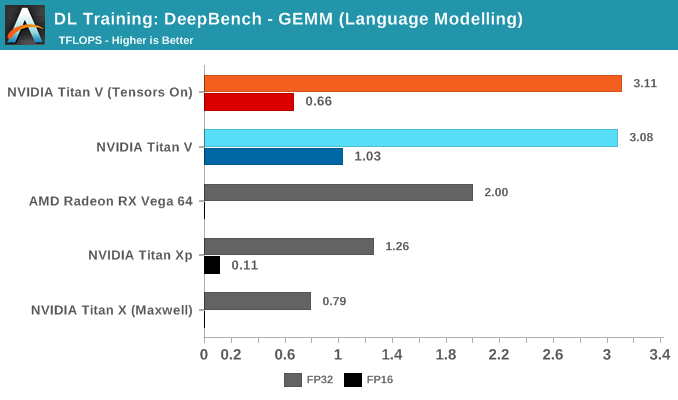
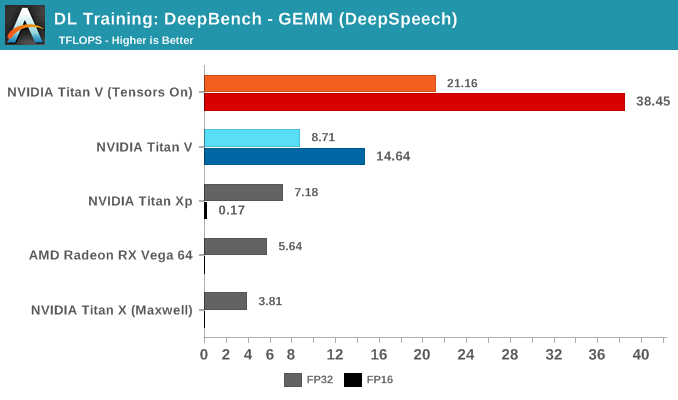
首先进行 GEMM 测试,利用某些深度学习应用程序(DeepSpeech、Speaker ID 和 Language Modeling)中的内核进行 GEMM 操作,测出的性能比在 cuBLAS 中运行纯矩阵-矩阵乘法更有代表性。
测试的结果在意料之内,启用 Tensor Core 可以大幅提升性能。深入研究细节可以发现,Tensor Core 对于特定类型的矩阵-矩阵乘法会有特别的影响。
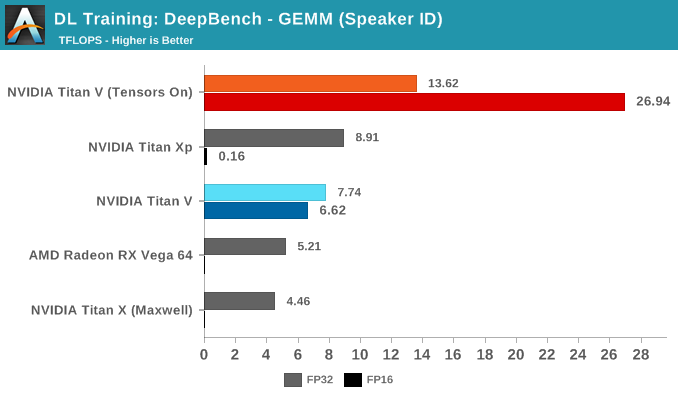
通过深度学习应用程序拆分 GEMM 测试,我们可以了解 Tensor Core 在理想和非理想情况下的表现。
Speaker ID GEMM 工作负载实际上只包含两个内核,其中 10 微秒的时间差意味着大约 1 TFLOPS 的算力差异。
通过对语言模型内核的研究,可以了解 Tensor Core 在非理想情况下的性能。这些核矩阵的大小是 m=512 或 1024,n=8 或 16,k=500000,虽然每个数在技术上都可以被8整除——这是满足张量核加速度的基本要求之一。但这些矩阵的形状与 Tensor Core 支持的 161616、32816 和 83216 等基本 WMMA 形状不太匹配。假如 Tensor Core 真正在独立的 8x8x8 级别上运行,那么运算 888 矩阵的性能也不会很好。
因此,Tensor Core 无法高效的将这些非常不平衡的矩阵分解为 n=8 或 16。而且,Tensor Core 在 DeepSpeech 内核上的性能也出现异常。
从所有子项的平均成绩来看,这个浮点运算性能令人印象深刻。当矩阵适合于 Tensor Core 时,性能可以超过 90TFLOPS;相反如果二者无法契合,并正确的换位没有发挥作用,性能会低至 <1TFLOPS 的水平。
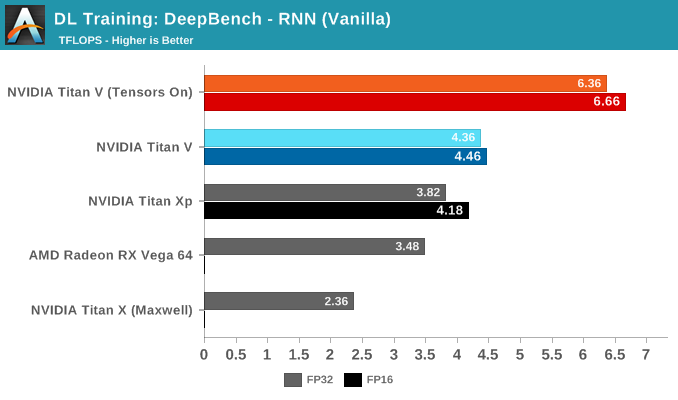
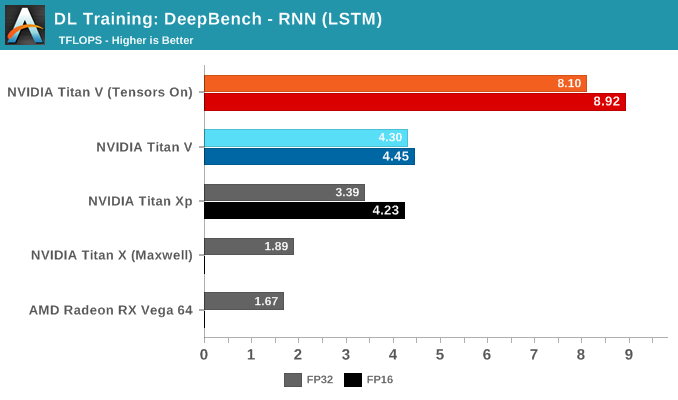
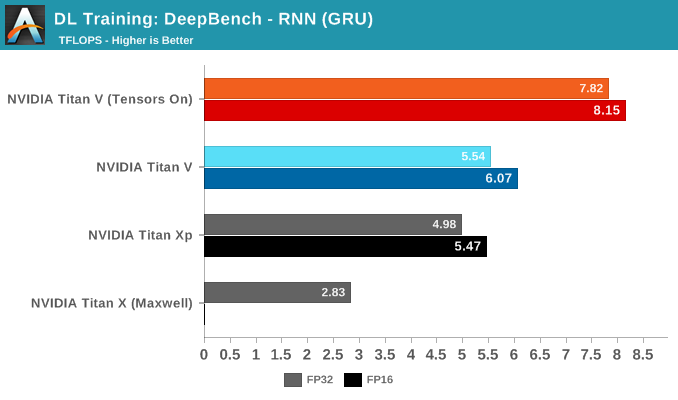
对于 DeepBench RNN 内核的测试,RNN类型之间没有明显的差异,但是在每种 RNN 类型中,如果将不同内核挨个进行对比判断,也可以看到与 GEMM 中相同的趋势。
比较有趣的是,Titan Xp 与 Titan V 在未使用 Tensor Core 加速时的表现有很接近,Titan Xp 的高频率为其性能起到了一定的帮助。
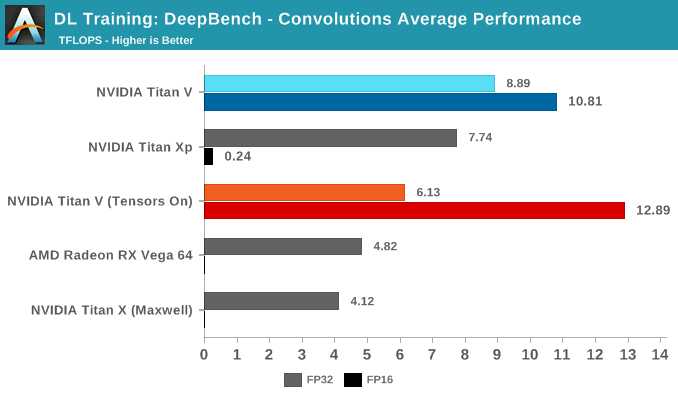
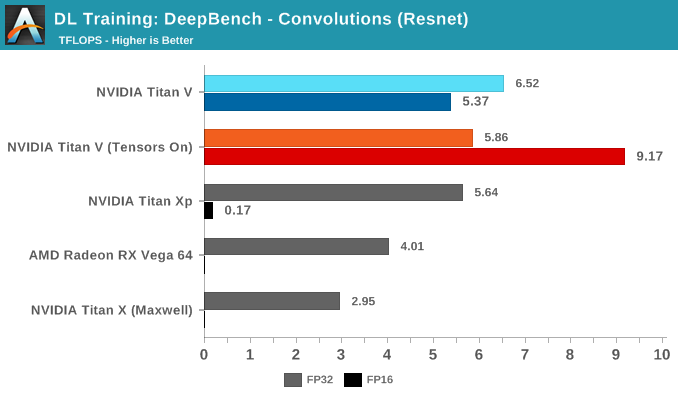
在卷积训练工作负载测试中,Tensor Core 再次显着提高了性能。鉴于卷积层是图像识别和分类的基础,因而卷积运算是 Tensor Core 加速的最大潜在受益者之一。
从所有测试项的平均成绩可以看出,Volta 在启用了 Tensor Core 的 FP16 混合精度运算能力后性能再次取得了领先。不过与 GEMM 不同,在 FP32 卷积上启用 Tensor Core 会导致明显的性能损失。
利用 Tensor Core 实现矩阵乘法的加速,一般有如下两种方式:
- 可以利用现成库函数,最新版本的 cuDNN 7.0,CUDA9.0 中的 cuBLAs,TensorRT 3.0 都支持 Tensor Core 的调用;其中 cuBLAS 主要加速了 GEMM 计算,cuDNN 里主要用来加速卷积和 RNN 。(该方式相对简单。)
- 在 CUDA 编程里实现 Tensor Core 的调用。新的 CUDA 9.0 里增加了 WMMA ,可以调用其中的API实现输入矩阵的 Load ,两个矩阵做乘加,还有结构矩阵的 Store 。(该方式相对复杂,但是更底层的实现,更符合我们的需求。)
以下是使用 WMMA 调用 Tensor Core 进行计算的示例。Tensor Cores 的调用 API 在nvcuda::wmma 命名空间里。通过调用 API 进行数值初始化,进行矩阵乘加(MMA)操作然后再把数值存回内存。具体见注释。
// 头文件 和 命名空间
#include<mma.h>
Using namespace nvcuda;
// The only dimensions currently supported by WMMA
// 单次 16*16 矩阵的乘法和累加称为 wmma 操作。
const int WMMA_M = 16;
const int WMMA_N = 16;
const int WMMA_K = 16;
__global__ void wmma_example(half *a, half *b, float *c,
int M, int N, int K,
float alpha, float beta)
{
// 定义wmma在各个方向上的维度(实际上就是单次计算的小矩阵(tile)的size)
// Leading dimensions. Packed with no transpositions.
// A[M, K] B[K, N] C[M, N]
int lda = M; // 矩阵 A 的行数
int ldb = K; // 矩阵 B 的行数
int ldc = M; // C 的行数(即 A 的行数)
// 【注意!】A,B的 size不局限于16*16,因为 16*16 只是单次 wmma 可运算的矩阵大小;
// 而通过多个 warp( SM 中的基本执行代码单元,包含 32 个 thread )和循环实现更大 size 的矩阵运算。
// Tile using a 2D grid
int warpM = (blockIdx.x * blockDim.x + threadIdx.x) / warpSize;
int warpN = (blockIdx.y * blockDim.y + threadIdx.y);
// 声明 fragment 变量
// Declare the fragments
// fragement变量用于对应一次wmma操作中的小矩阵块,声明时所填的参数表明了该fragment在计算中的用途和角色
// 声明规则如下。
// wmma::fragment<wmma 矩阵类型, (WMMA_M, WMMA_N, WMMA_K)三个参数用于表述数据的维度形状 , 矩阵数据类型(精度), wmma 存储类型(可选)> 变量名;
// 用于乘法的 matrix_a 和 matrix_b
wmma::fragment<wmma::matrix_a, WMMA_M, WMMA_N, WMMA_K, half, wmma::col_major> a_frag;
wmma::fragment<wmma::matrix_b, WMMA_M, WMMA_N, WMMA_K, half, wmma::col_major> b_frag;
// matrix_a 或 matrix_b 还必须说明数据在内存中的存储形式(如:wmma::col_major)是按行还是按列以方便 GPU 在读取数据时循环计算一系列 tile 的乘积。
// 附加项 和 输出矩阵 则定义为accumulator
wmma::fragment<wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> acc_frag;
wmma::fragment<wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> c_frag;
// Loop over the K-dimension
// 循环计算一系列 tile 的乘积
for (int i = 0; i < K; i += WMMA_K) {
// 利用 warp 的 ID 来决定这个 warp 所计算的 tile
int aRow = warpM * WMMA_M;
int aCol = i;
int bRow = i;
int bCol = warpN * WMMA_N;
// Bounds checking
if (aRow < M && aCol < K && bRow < K && bCol < N) {
// 计算之前需要使用在 wmma 命名空间下的 load_matrix_sync 函数加载数据,操作如下。
// wmma::load_matrix_sync(fragment 变量, 起始地址, leading dimension); 其中 leading dimension 表示数据在 按行存储时矩阵的总行数 或是 按列存储时的总列数 。
// 这样知道了输入矩阵的存储方式和 leading dimension 在加载数据时 GPU 可以知道如何在不连续的数据中取出我们需要的 tile 。
// Load the inputs
wmma::load_matrix_sync(a_frag, a + aRow + aCol * lda, lda);
wmma::load_matrix_sync(b_frag, b + bRow + bCol * ldb, ldb);
// 每次循环的结果都累加在 acc_fag 上。
// Perform the matrix multiplication
wmma::mma_sync(acc_frag, a_frag, b_frag, acc_frag);
// 最后 acc_frag 中的结果也就是结果矩阵 c 中该 warp 对应的 tile 。
}
}
}除了上述矩阵乘法以外,还可以在乘法结果上加一个附加项。 官方 blog 中同时也提到,在进行加法计算之前,乘法输出和附加矩阵都可以先进行 scale 也就是乘上一个系数。
// Load in current value of c, scale by beta, and add to result scaled by alpha
int cRow = warpM * WMMA_M;
int cCol = warpN * WMMA_N;
if (cRow < M && cCol < N) {
wmma::load_matrix_sync(c_frag, c + cRow + cCol * ldc, ldc, wmma::mem_col_major);
// num_elements 和 x[i] 都是 fragment 类的成员变量
for(int i=0; i < c_frag.num_elements; i++) {
c_frag.x[i] = alpha * acc_frag.x[i] + beta * c_frag.x[i];
}
}如下所示,其中 num_elements 和 x[i] 都是 fragment 类的成员变量,方便用户对fragment的数据进行逐一单独访问。
//num_elements和 x[i] 在 fragment 类中的定义
enum fragment<Use, m, n, k, T, Layout>::num_elements;
T fragment<Use, m, n, k, T, Layout>::x[num_elements];最后保存计算结果。
// Store the output
wmma::store_matrix_sync(c + cRow + cCol * ldc, c_frag, ldc, wmma::mem_col_major);
// 官方 blog 指出保存的地址可以为GPU上任意可见地址(及 shared memory 和 global memory )。这段代码是 Instant-NGP 使用 WMMA 调用 Tensor Core 进行计算的源码。在 CUDA 上执行神经网络前向传播过程中的一部分,具体来说是实现了一个输入层的前向传播。具体见注释。
template <int WIDTH, int N_ITERS, typename OUT_T, typename INPUT_LAYOUT>
// 使用了 template 模板参数来定义了当前线程块的宽度(WIDTH),迭代次数(N_ITERS),以及输出和输入数据类型(OUT_T 和 INPUT_LAYOUT)。
__device__ void threadblock_input_layer_forward_dynamic(Activation activation, __half* __restrict__ act_shmem, const __half* __restrict__ input_threadblock, const __half* __restrict__ weights_this_layer, OUT_T* __restrict__ out_intermediate_threadblock_this_layer, const uint32_t in_width, const uint32_t batch_size) {
// 激活函数的类型(activation),输入数据,权重矩阵,输出数据,输入宽度和批次大小。
// act_shmem contains the intermediate activations (shared memory) of the thread block's chunk of the batch
// input_threadblock points to the thread block's chunk of the input batch in global memory
// weights_this_layer points to the weight matrix of the current layer
// out_intermediate_threadblock_this_layer points to the location where intermediate activations produced by the thread block should be written to.
// Can be nullptr if nothing should be written.
// in_width is the dynamic width of the input layer
constexpr uint32_t SKEW = WIDTH % 16 == 0 ? 8 : 0;
constexpr uint32_t INPUT_SKEW = 8;
constexpr uint32_t N_BLOCKS = WIDTH / 16;
using namespace nvcuda;
// Fragments
// 它使用 nvcuda 命名空间定义了 wmma 类型的矩阵片段(fragment),包括矩阵 a(act_frag),矩阵 b(weights_frag)和累加器(result_frag)。
// 这些片段将在之后的代码中被用于进行矩阵乘法。
wmma::fragment<wmma::matrix_a, 16, 16, 16, __half, INPUT_LAYOUT> act_frag;
wmma::fragment<wmma::matrix_b, 16, 16, 16, __half, wmma::col_major> weights_frag;
wmma::fragment<wmma::accumulator, 16, 16, 16, OUT_T> result_frag[N_ITERS];
// Indices
// 线程在当前卷积核中的索引
const uint32_t li = threadIdx.x; // index in warp ("lane index")
const uint32_t wi = threadIdx.y; // index in block ("warp index")
// 计算矩阵乘法中的索引
const uint32_t lane_offset = (8 * li) % WIDTH;
const uint32_t row = (8 * li + wi * 8 * 32) / WIDTH;
// 表示权重矩阵中的一列
const uint32_t weights_col = 16 * wi;
// 一个指向共享内存的指针 weights_shmem,这将在之后的代码中用于加载权重矩阵
__half* __restrict__ weights_shmem = act_shmem + 16 * (in_width + INPUT_SKEW);
// Load input weight matrix (fits completely into shared memory)
// Each thread can load 8 fp16 elements (16 bytes) at once; we have N_BLOCKS warps
const uint32_t n_elems_per_load = N_BLOCKS * 32 * 8;
const uint32_t thread_elem_idx = (li + wi * 32) * 8;
const uint32_t n_elems_b = WIDTH * in_width;
// 主要是定义了一些变量和指针来加载权重矩阵。
TCNN_PRAGMA_UNROLL // 用于控制循环的宏
for (uint32_t idx = thread_elem_idx; idx < n_elems_b; idx += n_elems_per_load) {
const uint32_t idx_skewed = idx + idx / in_width * INPUT_SKEW;
*(int4*)&weights_shmem[idx_skewed] = *(int4*)&weights_this_layer[idx];
// 使用一个类型为 int4 的指针来读取 weights_this_layer 数组中的元素,并将其赋值给 weights_shmem 数组中对应的元素。
}
const uint32_t n_tensor_ops = in_width / 16;
if (std::is_same<INPUT_LAYOUT, wmma::col_major>::value) {
__syncthreads(); // 同步线程之间的操作。
}
TCNN_PRAGMA_UNROLL
for (int l = 0; l < N_ITERS; ++l) {
if (std::is_same<INPUT_LAYOUT, wmma::row_major>::value) {
// Load chunk of inputs into shmem.
// This is faster than loading it from gmem directly, even though it is only used once.
// (Possibly due to latency hiding through staging.)
const uint32_t n_elems_a = 16 * in_width;
TCNN_PRAGMA_UNROLL
for (uint32_t idx = thread_elem_idx; idx < n_elems_a; idx += n_elems_per_load) {
const uint32_t idx_skewed = idx + idx / in_width * INPUT_SKEW;
*(int4*)&act_shmem[idx_skewed] = *(int4*)&input_threadblock[l * n_elems_a + idx];
}
__syncthreads();
}
wmma::fill_fragment(result_frag[l], 0.0f);
// 结果矩阵中的元素都赋值为 0.0f
TCNN_PRAGMA_UNROLL
for (uint32_t i = 0; i < n_tensor_ops; ++i) {
// Load chunk of inputs and weights from shared memory and multiply them
// 从共享内存中加载一块输入数据和权重数据
if (std::is_same<INPUT_LAYOUT, wmma::row_major>::value) {
wmma::load_matrix_sync(act_frag, act_shmem + 16 * i, in_width + INPUT_SKEW);
} else {
wmma::load_matrix_sync(act_frag, input_threadblock + 16 * i * batch_size + 16 * l, batch_size);
}
wmma::load_matrix_sync(weights_frag, weights_shmem + 16 * i + weights_col * (in_width + INPUT_SKEW), in_width + INPUT_SKEW);
// 使用 wmma::mma_sync 函数来执行矩阵乘法运算,将结果累加到结果矩阵中。
wmma::mma_sync(result_frag[l], act_frag, weights_frag, result_frag[l]);
}
// 如果 INPUT_LAYOUT 的值为 wmma::row_major
if (std::is_same<INPUT_LAYOUT, wmma::row_major>::value) {
__syncthreads(); // 同步线程。
}
warp_activation<__half>(activation, result_frag[l], result_frag[l]);
}
if (std::is_same<INPUT_LAYOUT, wmma::col_major>::value) {
__syncthreads();
}
TCNN_PRAGMA_UNROLL
for (int l = 0; l < N_ITERS; ++l) {
wmma::store_matrix_sync(act_shmem + weights_col + (16 * l) * (WIDTH + SKEW), result_frag[l], WIDTH + SKEW, wmma::mem_row_major);
// 在 Shared Memory 中存储一个矩阵,并且同步所有线程。
// act_shmem 是 Shared Memory 的指针,weights_col 是列偏移量, result_frag[l] 是矩阵, WIDTH 和 SKEW 是常量。
}
if (out_intermediate_threadblock_this_layer != nullptr) {
__syncthreads();
TCNN_PRAGMA_UNROLL
for (int i = 0; i < N_ITERS; ++i) {
*(int4*)&out_intermediate_threadblock_this_layer[lane_offset + (row + 16 * i) * WIDTH] = *(int4*)&act_shmem[lane_offset + (row + 16 * i) * (WIDTH + SKEW)];
// 会将 Shared Memory 中的数据复制到 out_intermediate_threadblock_this_layer 中,其中 lane_offset 是偏移量,row 是行偏移量
}
}
}参考部分文献/网页等如下。
The NVIDIA Titan V Deep Learning Deep Dive: It's All About The Tensor Cores.
NVIDIA深度学习Tensor Core全面解析。
NVIDIA Tensor Core深度学习核心解析。
理解Tensor Core
Tensor Core有多牛?
英伟达官方解读:Volta Tensor Core GPU实现AI性能新里程碑