- New activation function (sin, cos, tan, GeLU) with optimizable bounds (α-CROWN) and branch and bound support for non-ReLU activation functions. We achieve significant improvements on verifying neural networks with non-ReLU activation functions such as Transformer and LSTM networks. (09/2023)
- α,β-CROWN (alpha-beta-CROWN) (using
auto_LiRPAas its core library) won VNN-COMP 2023. (08/2023) - Bound computation for higher-order computational graphs to support bounding Jacobian, Jacobian-vector products, and local Lipschitz constants. (11/2022)
- Our neural network verification tool α,β-CROWN (alpha-beta-CROWN) (using
auto_LiRPAas its core library) won VNN-COMP 2022. Our library supports the large CIFAR100, TinyImageNet and ImageNet models in VNN-COMP 2022. (09/2022) - Implementation of general cutting planes (GCP-CROWN), support of more activation functions and improved performance and scalability. (09/2022)
- Our neural network verification tool α,β-CROWN (alpha-beta-CROWN) won VNN-COMP 2021 with the highest total score, outperforming 11 SOTA verifiers. α,β-CROWN uses the
auto_LiRPAlibrary as its core bound computation library. (09/2021) - Optimized CROWN/LiRPA bound (α-CROWN) for ReLU, sigmoid, tanh, and maxpool activation functions, which can significantly outperform regular CROWN bounds. See simple_verification.py for an example. (07/31/2021)
- Handle split constraints for ReLU neurons (β-CROWN) for complete verifiers. (07/31/2021)
- A memory efficient GPU implementation of backward (CROWN) bounds for convolutional layers. (10/31/2020)
- Certified defense models for downscaled ImageNet, TinyImageNet, CIFAR-10, LSTM/Transformer. (08/20/2020)
- Adding support to complex vision models including DenseNet, ResNeXt and WideResNet. (06/30/2020)
- Loss fusion, a technique that reduces training cost of tight LiRPA bounds (e.g. CROWN-IBP) to the same asympototic complexity of IBP, making LiRPA based certified defense scalable to large datasets (e.g., TinyImageNet, downscaled ImageNet). (06/30/2020)
- Multi-GPU support to scale LiRPA based training to large models and datasets. (06/30/2020)
- Initial release. (02/28/2020)
auto_LiRPA is a library for automatically deriving and computing bounds with
linear relaxation based perturbation analysis (LiRPA) (e.g.
CROWN and
DeepPoly) for
neural networks, which is an useful tool for formal robustness verification. We
generalize existing LiRPA algorithms for feed-forward neural networks to a
graph algorithm on general computational graphs, defined by PyTorch.
Additionally, our implementation is also automatically differentiable,
allowing optimizing network parameters to shape the bounds into certain
specifications (e.g., certified defense). You can find a video
Our library supports the following algorithms:
- Backward mode LiRPA bound propagation (CROWN/DeepPoly)
- Backward mode LiRPA bound propagation with optimized bounds (α-CROWN)
- Backward mode LiRPA bound propagation with split constraints (β-CROWN) for ReLU, and (Shi et al. 2023) for general nonlinear functions
- Generalized backward mode LiRPA bound propagation with general cutting plane constraints (GCP-CROWN)
- Forward mode LiRPA bound propagation (Xu et al., 2020)
- Forward mode LiRPA bound propagation with optimized bounds (similar to α-CROWN)
- Interval bound propagation (IBP)
- Hybrid approaches, e.g., Forward+Backward, IBP+Backward (CROWN-IBP), α,β-CROWN (alpha-beta-CROWN)
Our library allows automatic bound derivation and computation for general
computational graphs, in a similar manner that gradients are obtained in modern
deep learning frameworks -- users only define the computation in a forward
pass, and auto_LiRPA traverses through the computational graph and derives
bounds for any nodes on the graph. With auto_LiRPA we free users from
deriving and implementing LiPRA for most common tasks, and they can simply
apply LiPRA as a tool for their own applications. This is especially useful
for users who are not experts of LiRPA and cannot derive these bounds manually
(LiRPA is significantly more complicated than backpropagation).
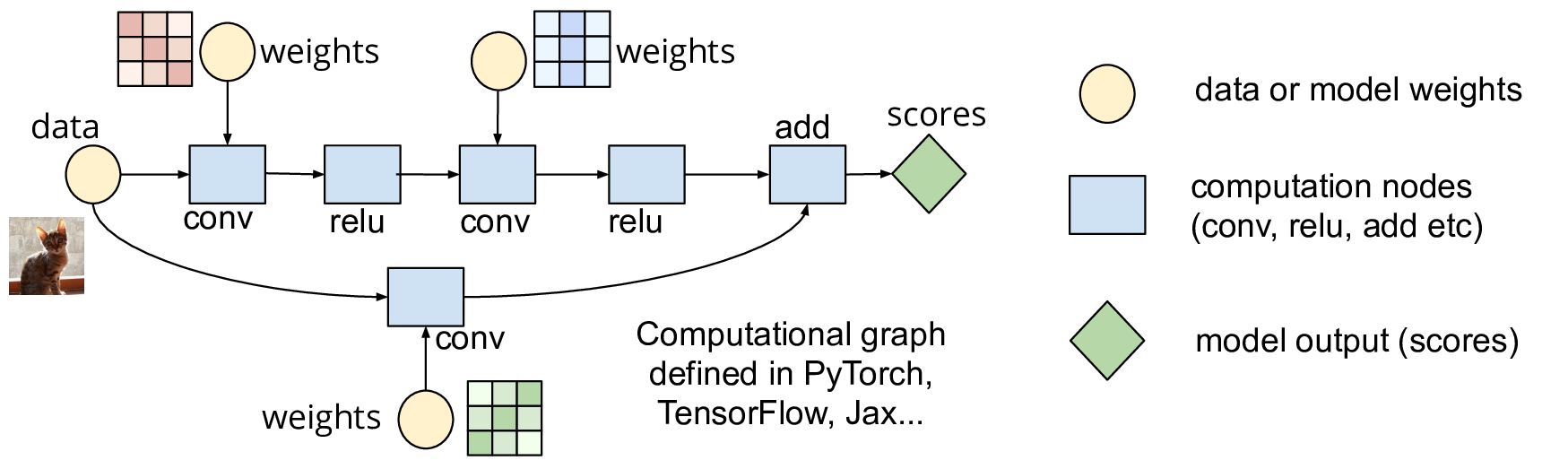
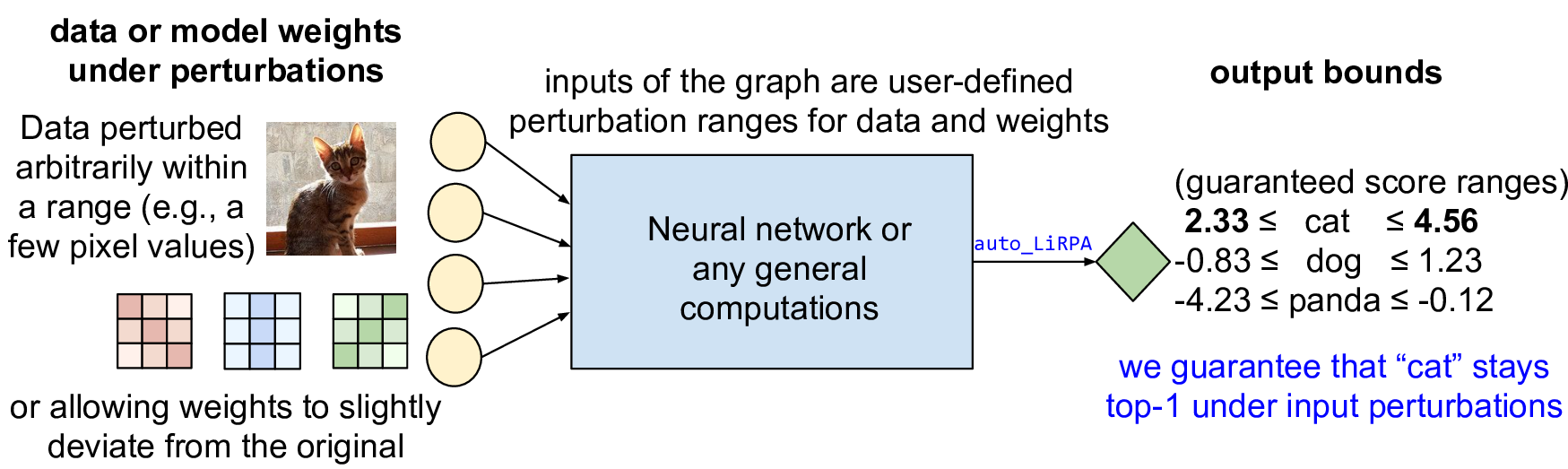
Deep learning frameworks such as PyTorch represent neural networks (NN) as a computational graph, where each mathematical operation is a node and edges define the flow of computation:
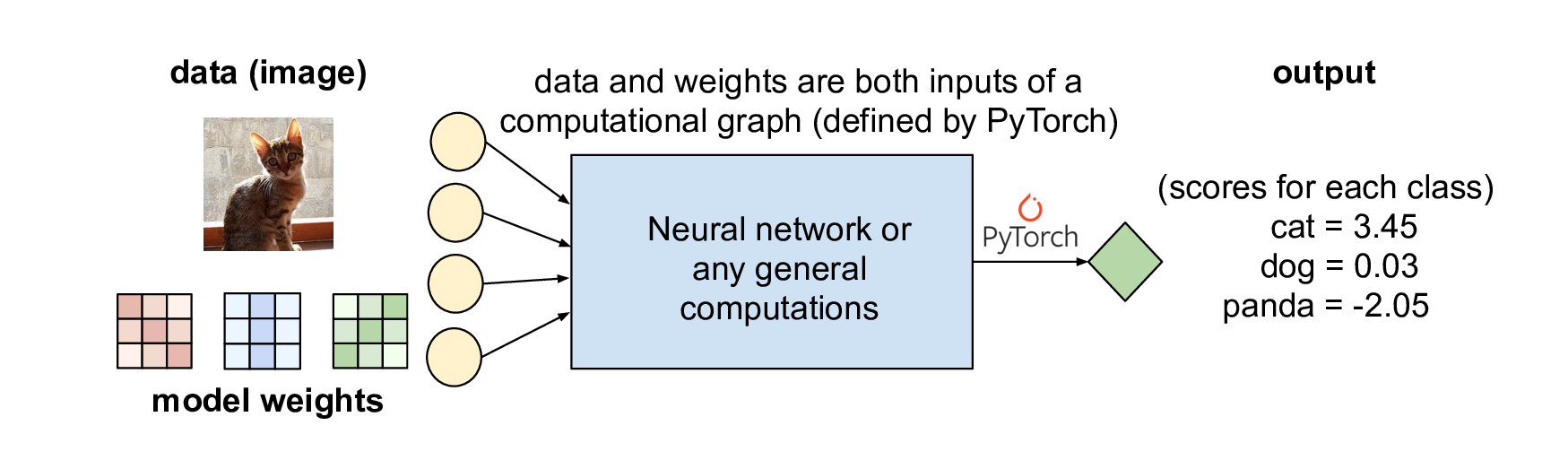
Normally, the inputs of a computation graph (which defines a NN) are data and model weights, and PyTorch goes through the graph and produces model prediction (a bunch of numbers):
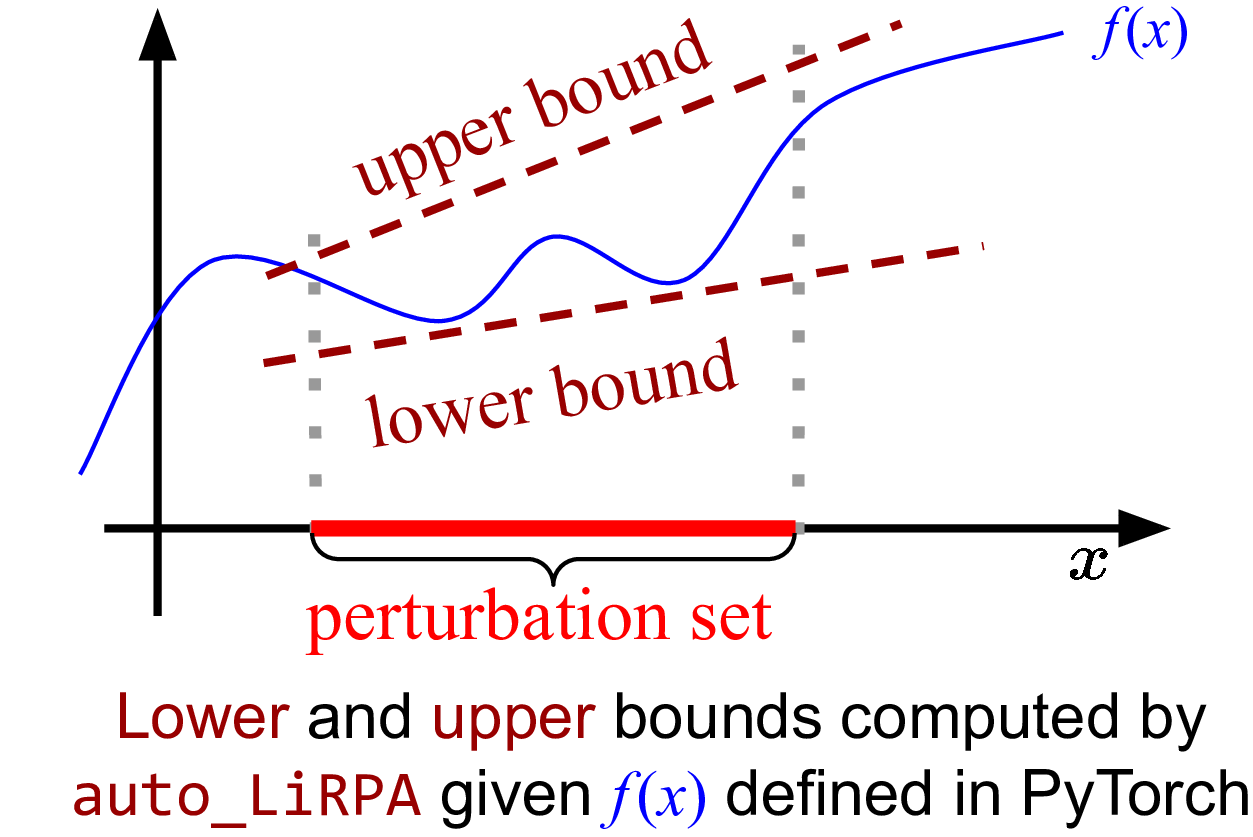
Our auto_LiRPA library conducts perturbation analysis on a computational
graph, where the input data and model weights are defined within some
user-defined ranges. We get guaranteed output ranges (bounds):
Python 3.7+ and PyTorch 1.11+ are required.
PyTorch 1.11 is recommended, although other recent versions might also work.
It is highly recommended to have a pre-installed PyTorch
that matches your system and our version requirement.
See PyTorch Get Started.
Then you can install auto_LiRPA via:
git clone https://github.com/Verified-Intelligence/auto_LiRPA
cd auto_LiRPA
python setup.py installIf you intend to modify this library, use python setup.py develop instead.
Optionally, you may build and install native CUDA modules (CUDA toolkit required):
python auto_LiRPA/cuda_utils.py installFirst define your computation as a nn.Module and wrap it using
auto_LiRPA.BoundedModule(). Then, you can call the compute_bounds function
to obtain certified lower and upper bounds under input perturbations:
from auto_LiRPA import BoundedModule, BoundedTensor, PerturbationLpNorm
# Define computation as a nn.Module.
class MyModel(nn.Module):
def forward(self, x):
# Define your computation here.
model = MyModel()
my_input = load_a_batch_of_data()
# Wrap the model with auto_LiRPA.
model = BoundedModule(model, my_input)
# Define perturbation. Here we add Linf perturbation to input data.
ptb = PerturbationLpNorm(norm=np.inf, eps=0.1)
# Make the input a BoundedTensor with the pre-defined perturbation.
my_input = BoundedTensor(my_input, ptb)
# Regular forward propagation using BoundedTensor works as usual.
prediction = model(my_input)
# Compute LiRPA bounds using the backward mode bound propagation (CROWN).
lb, ub = model.compute_bounds(x=(my_input,), method="backward")Checkout examples/vision/simple_verification.py for a complete but very basic example.
We also provide a Google Colab Demo including an example of computing verification
bounds for a 18-layer ResNet model on CIFAR-10 dataset. Once the ResNet model
is defined as usual in Pytorch, obtaining provable output bounds is as easy as
obtaining gradients through autodiff. Bounds are efficiently computed on GPUs.
We provide a wide range of examples of using auto_LiRPA:
- Basic Bound Computation and Robustness Verification of Neural Networks
- Basic Certified Adversarial Defense Training
- Large-scale Certified Defense Training on ImageNet
- Certified Adversarial Defense Training on Sequence Data with LSTM
- Certifiably Robust Language Classifier using Transformers
- Certified Robustness against Model Weight Perturbations
- Bounding Jacobian and local Lipschitz constants
auto_LiRPA has also be used in the following works:
- α,β-CROWN for complete neural network verification
- Fast certified robust training
- Computing local Lipschitz constants
For more documentations, please refer to:
- Documentation homepage
- API documentation
- Adding custom operators
- Guide for reproducing our NeurIPS 2020 paper
Please kindly cite our papers if you use the auto_LiRPA library. Full BibTeX entries can be found here.
The general LiRPA based bound propagation algorithm was originally proposed in our paper:
- Automatic Perturbation Analysis for Scalable Certified Robustness and Beyond. NeurIPS 2020 Kaidi Xu*, Zhouxing Shi*, Huan Zhang*, Yihan Wang, Kai-Wei Chang, Minlie Huang, Bhavya Kailkhura, Xue Lin, Cho-Jui Hsieh (* Equal contribution)
The auto_LiRPA library is further extended to allow optimized bound (α-CROWN), split constraints (β-CROWN) general constraints (GCP-CROWN), and higher-order computational graphs:
-
Fast and Complete: Enabling Complete Neural Network Verification with Rapid and Massively Parallel Incomplete Verifiers. ICLR 2021. Kaidi Xu*, Huan Zhang*, Shiqi Wang, Yihan Wang, Suman Jana, Xue Lin and Cho-Jui Hsieh (* Equal contribution).
-
Beta-CROWN: Efficient Bound Propagation with Per-neuron Split Constraints for Complete and Incomplete Neural Network Verification. NeurIPS 2021. Shiqi Wang*, Huan Zhang*, Kaidi Xu*, Suman Jana, Xue Lin, Cho-Jui Hsieh and Zico Kolter (* Equal contribution).
-
GCP-CROWN: General Cutting Planes for Bound-Propagation-Based Neural Network Verification. Huan Zhang*, Shiqi Wang*, Kaidi Xu*, Linyi Li, Bo Li, Suman Jana, Cho-Jui Hsieh and Zico Kolter (* Equal contribution).
-
Efficiently Computing Local Lipschitz Constants of Neural Networks via Bound Propagation. NeurIPS 2022. Zhouxing Shi, Yihan Wang, Huan Zhang, Zico Kolter, Cho-Jui Hsieh.
Certified robust training using auto_LiRPA is improved to allow much shorter warmup and faster training:
- Fast Certified Robust Training with Short Warmup. NeurIPS 2021. Zhouxing Shi*, Yihan Wang*, Huan Zhang, Jinfeng Yi and Cho-Jui Hsieh (* Equal contribution).
Branch and bound for non-ReLU and general activation functions:
- Formal Verification for Neural Networks with General Nonlinearities via Branch-and-Bound. Zhouxing Shi*, Qirui Jin*, Zico Kolter, Suman Jana, Cho-Jui Hsieh, Huan Zhang (* Equal contribution).
Team lead:
- Huan Zhang (huan@huan-zhang.com), UIUC
Current developers:
- Zhouxing Shi (zshi@cs.ucla.edu), UCLA
- Linyi Li (linyi2@illinois.edu), UIUC
- Christopher Brix (brix@cs.rwth-aachen.de), RWTH Aachen University
- Kaidi Xu (kx46@drexel.edu), Drexel University
- Xiangru Zhong (xiangruzh0915@gmail.com), Sun Yat-sen University
- Qirui Jin (qiruijin@umich.edu), University of Michigan
- Zhuolin Yang (zhuolin5@illinois.edu), UIUC
- Zhuowen Yuan (realzhuowen@gmail.com), UIUC
Past developers:
- Shiqi Wang (sw3215@columbia.edu), Columbia University
- Yihan Wang (yihanwang@ucla.edu), UCLA
- Jinqi (Kathryn) Chen (jinqic@cs.cmu.edu), CMU
We thank the commits and pull requests from community contributors.
Our library is released under the BSD 3-Clause license.
This is a fork for our work.