===============================================================================
=================[ QOCS - Quantum OCaml Circuit Simulator ]====================
===============================================================================
---[ RUNNING ]---
To run QOC, simply unzip the source files, and type "make" in the terminal.
To clean the compiled files, simply run "make clean" in the terminal.
---[ EXAMPLES of simulator ]---
Here are some examples of gates that one could make using QOCS. Run the
following commands after running make to see the results!
1. Hadamards
s - Enter simulator
c - Enter circuit building mode
H 0 H 1 H 2 - Make the hadamard gates by listing each H
save - Save the gate...
hadamards - as "hadamards"
q - Quit circuit building mode
a - Enter apply mode
hadamards [1,0,0,0,0,0,0,0] - Apply the hadamard state to |000>, and see
results.
After that, you should see a normalized state with all of the qubits
with equal amplitudes!
q - Quit apply mode
q - Quit simulator
q - Quit QOCS
2. Toffoli using U and CNOT
s - Enter simulator
c - Enter circuit building mode
u y 0 pi/4 cnot 1 0
u y 0 pi/4 cnot 2 0
u y 0 -pi/4 cnot 1 0
u y 0 -pi/4 (one line) - Make the tof gate
save - Save the gate...
tof - as "tof"
q - Quit circuit building mode
a - Enter apply mode
tof [0,0,0,0,0,0,1,0] - Apply the tof gate to |000>, and see results.
q - Quit apply mode
q - Quit simulator
q - Quit QOCS
3. GHZ state
s - Enter simulator
c - Enter circuit building mode
h 1 cnot 1 0 - To make the gate for GHZ state
save - Save the gate...
ghz - as "ghz"
q - Quit circuit building mode
a - Enter apply mode
ghz [1,0,0,0] - Apply the tof gate to |00>, and see results.
q - Quit apply mode
q - Quit simulator
q - Quit QOCS
---[ Factoring ]---
You can also enter factoring mode. Factor allows you factor a number of type
x = p*q where p and q are prime numbers, such as x = 15. Factoring mode uses
quantum computers and Quantum Fourier Transform the factor the number, instead
of calculating it classically.
We will be building QOCS (Quantum OCaml Circuit Simulator), a functional approach to simulating quantum gates. QOCS will serve as a tool for building quantum circuits, whose potential ranges from breaking RSA encryption to performing quantum Fourier transforms, and as a debugging tool for designing circuits and measuring run-time information of various quantum computing algorithms.
-
Implement arbitrary number of quantum gates.
-
Take in as input arbitrary n-qubit states where n is limited by the host computer’s memory.
-
Have pre-made functions specifically for performing Shor’s algorithm as a proof of effectiveness.
More attention is being paid to quantum computing after the advent of quantum algorithms that drastically speed up classical computing problems. One example is Shor’s algorithm for factoring products of prime numbers. It was one of the first quantum algorithms that demonstrated such an improvement for an important problem, decreasing the time complexity from exponential to polynomial time. Here, we charter an implementation of a quantum circuit emulator in OCaml that can be used to simulate not just Shor’s algorithm, but any quantum algorithm, given enough host memory.
QOCS will take an arbitrary n-qubit state as the input state and an input string that defines a specific quantum circuit to be simulated. The program will then implement said circuit using CNOT gates and single qubit unitary gates and produce the output state of the qubits. It is a mathematical fact that CNOT gates and single qubit unitary gates are universal: meaning that their combinations can produce any n-qubit gate to arbitrary precision. This allows us to simulate any quantum circuit. However, because of the amount of memory required to keep track of the system grows exponentially in the number of qubits, the number of qubits QOCS can simulate will be limited by the amount of memory in the host computer. For building circuits, we provide the CNOT gate and elementary unitary transformation gates. However, to simplify computation, we also provide the Toffoli gate and any n-qubit controlled gate.
As a proof of concept, we will implement a built in function to specifically simulate Shor’s algorithm that will be able to factor small products of prime numbers. Once again, the reason that we cannot factor large products is that the amount of memory required is roughly exponential in the size of the number for a classical computer. Note that Shor’s algorithm will also require some other helper functions that carry out the non-quantum but number-theoretic steps of the algorithm. Because it is an intermediate step in Shor’s algorithm, we will also implement the Quantum Fourier Transform.
A quick tutorial on how to use the program will be provided.
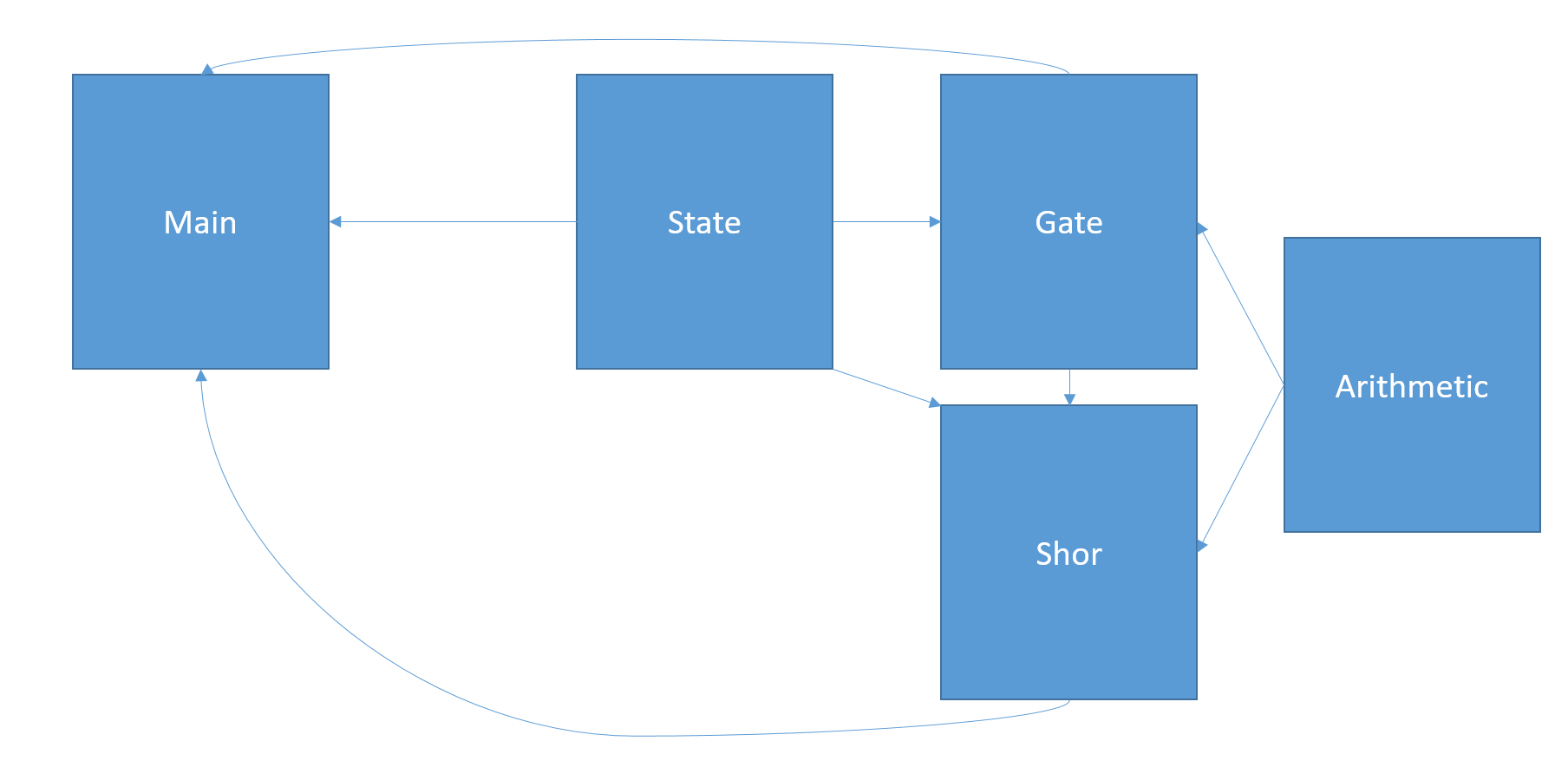
QOCS will be a pipe and filter system as shown in [fig:cc]. Upon startup, the program will process user input into two possible pipes; the user can either use Shor’s algorithms for factoring or create his own circuit through a REPL.
If the user chooses to run a built in quantum algorithm, the program will take in the arguments of the algorithm and output the final result as well as relevant information about the algorithm.
On the other hand, if the user chooses to build and run their own quantum circuit, QOCS will ask the user to first build the circuit and save it. It will then ask for an input state as well as the name of the saved circuit. Then it will run the algorithm and return the output state of the circuit as well as relevant statistics. The user will then be taken back to the REPL and will be able to restart the process.
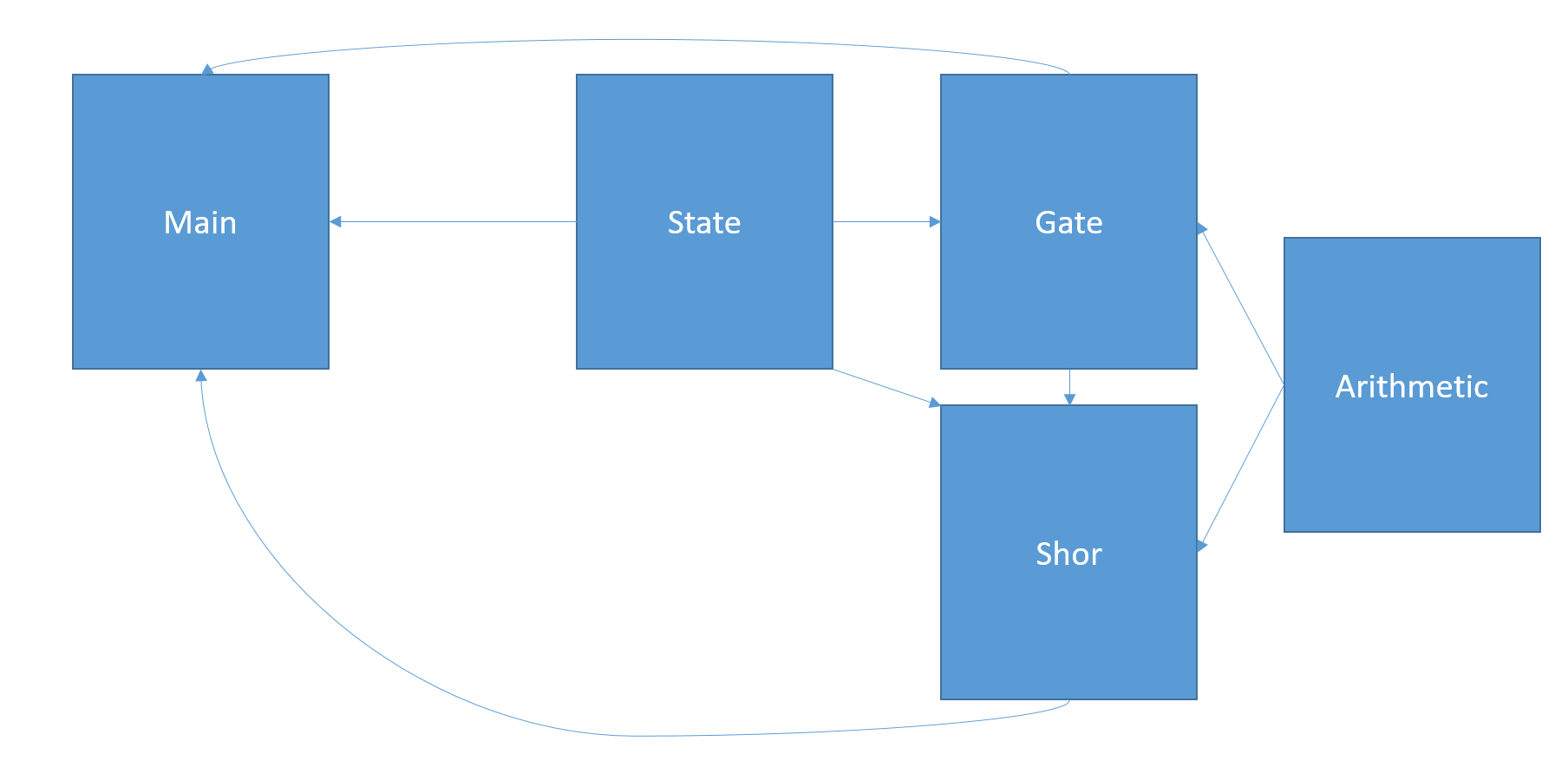
Our project has 5 modules, including the main module. Their dependency is visualized in [fig:mdd]. Here is a brief summary of the purpose of each module:
-
Arithmetic: Consists of required arithmetic and number theoretic functions that are required to implement specific gates and parts of Shor’s factoring algorithm. Details in “arithmetic.mli” file.
-
State: Consists of required types and functions for a quantum state. This will implement qubits in the quantum computer to be processed by other functions in other modules. Details in “state.mli” file.
-
Gate: Consists of required types and functions for a quantum gate. A gate is essentially an operator that takes in a state and outputs a state, much like how a classical logic gate. Therefore this module makes use of the states created by the State module. Multiple gates can be composed to form a composite gate. Depends on Arithmetic module. Details in “gate.mli” file.
-
Shor: Consists of required functions to implement Shor’s factoring algorithm. Requires both quantum states and quantum gates to implement and run the algorithm. Depends on Arithmetic module. Details in “shor.mli” file.
-
Main: Runs the REPL which provides the user with 2 choices: either build circuits and apply states to them OR factor integers. Depends on the Gate, State and Shor module’s because the user can create their own quantum gates through input, apply gates to states or factor integers (which uses Shor’s factoring algorithm).
The user should be able to use this software to pre-program quantum gates, built from elementary gates, to use in the future. For example, the Toffoli gate, which is essential for building most of the useful quantum computing circuits, is not yet defined as a basic gate that the user will be able to use from the very beginning. Since these gates are tedious to build over and over again whenever a Toffoli gate is required, it made sense in our design to have a system that will be able to store and load predefined gates.
Whenever the user decides to enter the REPL in the program, the program
will automatically upload the gates that were previously defined and
saved. A sample method of defining and storing gates could be something
like these commands:
> X 0 1 Y 1 0 ...etc... > Save > Toffoli
To save Toffoli, the details of the Toffoli gate will be saved in a
textfile along with the name, which can be loaded up to be used in the
future.
-
Random
Since quantum states exist in superpositions, with various probabilities associated with each states, we need to employ some sort of random number generator to be able to collapse the states during measurement.
-
Complex
The coefficients for each quantum state need to be stored as a complex number, since each state is associated with an amplitude of the probability, as well as its phase. Using the Complex module makes it very easy to perform numerical calculations between complex numbers.
-
List
During development, each quantum state will be stored as a list of complex numbers representing the coefficients of each qubits. Having List methods such as foldleft and map could be very useful in consolidating our code.
-
ANSITerminal
The REPL that we will design for the quantum computer will look a lot better if it is color coded.
-
String
For processing and manipulating strings.
-
Str
For parsing user input using regular expressions.
The methods of testing our code are fairly simple.
-
We plan to program Shor’s Algorithm as a canonical use of quantum computers. Testing our code on Shor with increasing number of qubits would be a good way of testing both the run-time and the memory usage of our code. Within the Shor module, we plan to test each helper function immediately after they are written. A second test for these helper functions is whether or not the algorithm factors correctly in the end.
-
Due to the nature of this project, every component of QOCS is highly modular since we are designing individual gates for the program. Therefore, performing Monte-Carlo simulations on the results of various quantum circuits could be used as a way to benchmark our codes. For example, measuring a large number of times on a zero state acted by a Hadamard will return the zero state half of the time, and the one state the other half of the time. Any sort of measurement gate circuits will require a Monte-Carlo test.
-
Here are some of the gates that we will use to test our code. These gates are described in Quantum Computer Science by David Mermin, and are the core gates that are required for a useful quantum computer.
-
$U_f$ for Shor -
Gate for Quantum Fourier Transform
-
Toffoli using U rotation gates and CNOTs
-
Swap gate using fundamental X, Y, and Z gate.
-
General Hadamard gate using individual Hadamards
-
Circuit to send information using Bell states
-
$2^4$ possible gates for 2-qubit to 1-qubit functions -
Toffoli gate using Phase and CNOT gates
-
Circuit to add two 2-bit numbers
-
The following circuit identities
-
$C X_0 C = X_0 X_1$ -
$C Z_0 C = Z_0$ -
$C Y_1 C = Z_0 Y_1$ -
$u_0(\hat{z},\theta)C=C u_0 (\hat{z},\theta)$
-
-
Circuit to create a 3 qubit GHZ state
-
-
We will hold each responsible for the testing of his own modules. Once all the modules are completed, we test the final product, through our own REPL. We also will show off our final product to other students in other classes, asking them to give satisfaction reviews and to find any other run-time bugs that we might have missed out on.
-
Successfully created an accurate simulation of a quantum computer up to 19 qubits.
-
Implemented a recursive variant structure as a tree to implement quantum gates.
-
Used a tree-like structure successfully alter states and implement fundamental quantum gates like X, Y, Z or Hadamards.
-
Implemented the non-elementary
$U_f$ gate for future developers to use with arbitrary functions$f$ . -
Successfully implemented a REPL for the user to build circuits using gates and to apply these circuits to states or to factor integers.
-
Implemented functionality to save circuits to an external file so that they can be used even when the REPL is closed and run again.
-
Implemented the Quantum Fourier Transform circuit for future developers.
-
Implemented Shor’s factoring algorithm which is theoretically capable of factoring any product of distinct primes, given enough time. Also prints useful statements for the user to follow throughout the routine.
-
Not bug but feature: Takes very long time to factor products of
distinct primes above greater than 22. This is because the
$U_f$ gate acts on every single term in the superposition of an input state, requiring$2^n$ operations classically where$n$ is the number of total qubits. The total number of qubits required to factor an integer$i$ is equal to$3*n_0$ where$n_0$ is the smallest integer such that$2^{n_0} > i$ . Hence factoring an integer like$33$ requires at least one traversal of$2^{18}$ elements. However, with a quantum computer, this would take constant time due to “quantum parallelism”. This is one example of why we cannot efficiently simulate quantum computers using classical computer. We must build physically quantum systems to effectively implement these kinds of quantum algorithms.
Implemented Shor and Arithmetic module. The former contains Shor’s
period finding algorithm including creation and application of the
quantum circuit and the number theoretic post-processing functions for
factoring products of distinct primes. The latter contains functions
necessary for performing base
Implemented Gate and State modules, which become the back-end modules for calculating qubit states and passing states through gates. Other modules like Shor rely on Gate and State in order to perform the necessary calculations.
Implemented Main module. This module runs the REPL and all actions associated with it. These actions include: parsing circuit and gate inputs from the user, parsing state application to gates, parsing tensor products of states, saving circuits and parsing integers to factor.