This repository contains the code used to generate the results of the research article
David Melching, Tobias Strohmann, Florian Paysan and Eric Breitbarth.
An iterative crack tip correction algorithm discovered by physical deep symbolic regression.
International Journal of Fatigue 187 (2024) 108432.
The article is published here. All data resulting from this study is available on Zenodo.
Digital image correlation is a widely used technique in the field of experimental mechanics. In fracture mechanics, determining the precise location of the crack tip is crucial. In this paper, we introduce a universal crack tip detection algorithm based on displacement and strain fields obtained by digital image correlation. Iterative crack tip correction formulas are discovered by applying deep symbolic regression guided by physical unit constraints to a dataset of simulated cracks under mode I, II and mixed-mode conditions with variable T-stress. For the training dataset, we fit the Williams series expansion with super-singular terms to the simulated displacement fields at randomly chosen origins around the actual crack tip. We analyse the discovered formulas and apply the most promising one to digital image correlation data obtained from uniaxial and biaxial fatigue crack growth experiments of AA2024-T3 sheet material. Throughout the experiments, the crack tip positions are reliably detected leading to improved stability of the crack propagation curves.
- Python 3.11
- Ansys Mechanical: To run the simulations, we used Ansys Mechanical APDL 2023 R1.
- CrackPy: We used CrackPy version 1.2.0 to determine the Williams coefficients.
- PhySO: We used PhySO version v1.0.0 to perform symbolic regression.
- Create a virtual environment of Python 3.11 and activate it.
- Install the required packages using the following command:
pip install -r requirements.txt- Install the CrackPy package using the following command:
pip install git+https://github.com/dlr-wf/crackpy.git@1.2.0- Install the PhySO package using the following command:
pip install git+https://github.com/WassimTenachi/PhySO.git@v1.0.0The repository contains the following folders:
cracktipcorr: The main package containing the code for crack tip correction.docs: Documentation folder containing images for this README.scripts_paper: The scripts used to generate results and particularly the plots of the paper.
In addition, the repository contains script, which should be executed consecutively to generate the results:
01_finite_element_model.py: Generate FE data using Ansys Mechanical and pyansys.
 |
 |
|---|---|
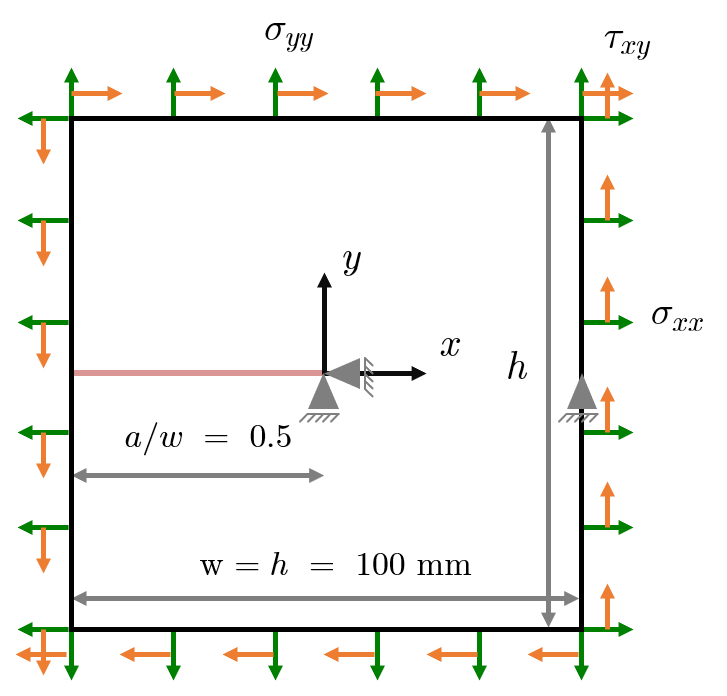
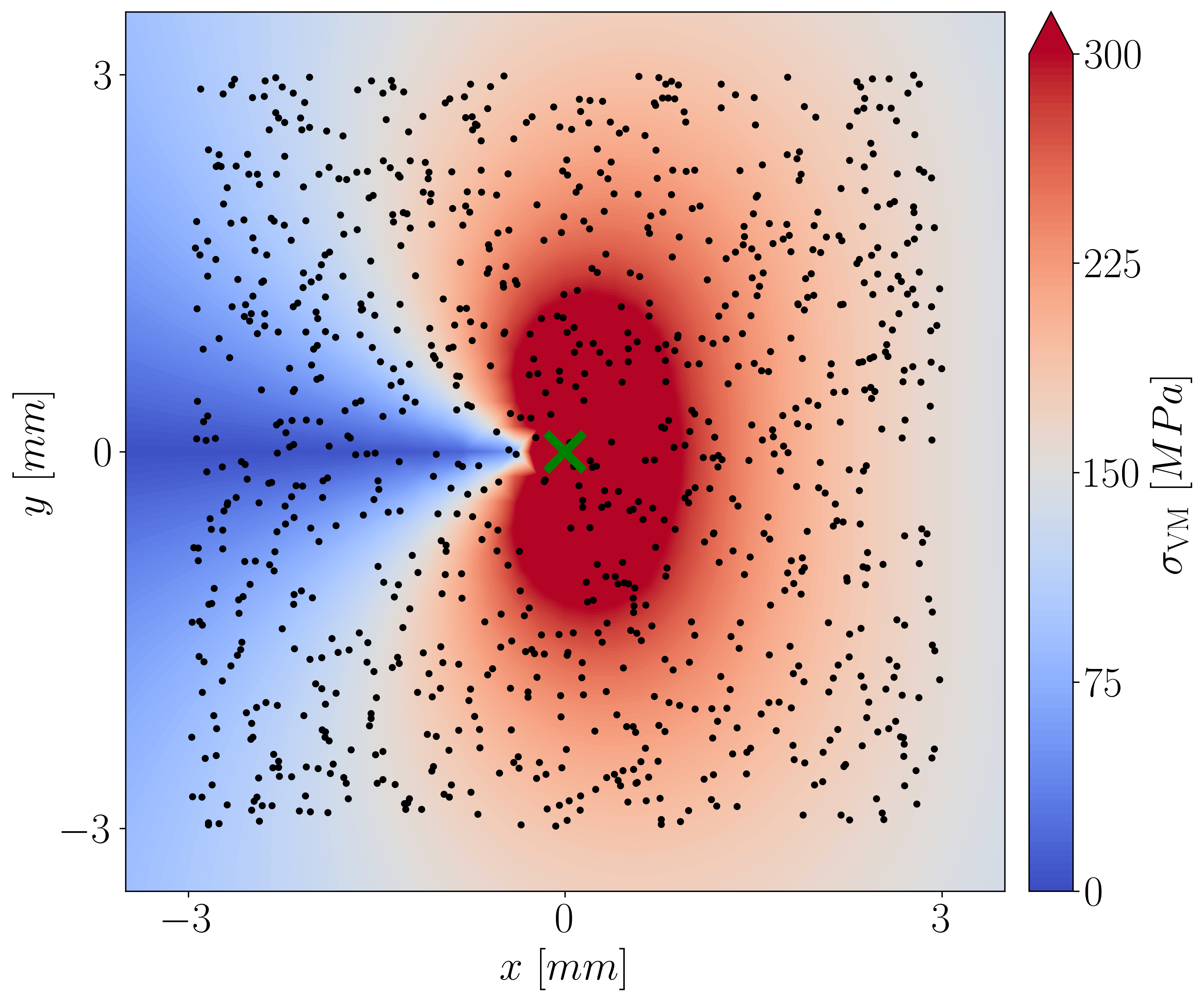
| Finite element model for the simulations | Random samples overlayed with the von Mises stress |
The script goes through several load cases and saves the displacement and strain data ("nodemaps")
together with plots of the mesh, displacements and von Mises stress in a folder called 01_Simulation_Output.
04_crackpy_random_evaluation_pipeline.py: Run CrackPy for 1000 randomly shifted crack tip positions for each nodemaps in 01_Simulation_Output folder.
The results are saved in a folder called 04_CrackPy_random_evaluation_pipeline.
We are particularly interested in the Williams coefficients, which are determined by fitting the theoretical field to
the simulation data.
Our goal is to learn a crack tip correction function taking the Williams coefficients as input and outputting the correction vector to arrive at the actual crack tip position. We use the PhySO package [REF] to train a symbolic regression model to learn this function from the simulation data.
05_1_SymbolicRegression_PhySO_mode_I.py: Perform symbolic regression only using mode I load cases.05_2_SymbolicRegression_PhySO_mode_II.py: Perform symbolic regression only using mode II load cases.05_3_SymbolicRegression_PhySO_mixed_mode.py: Perform symbolic regression using all load cases (mode I, mode II, and mixed mode).
The results are saved in folders called 05_1_PhySO_log_mode_I, 05_2_PhySO_log_mode_II, and 05_3_PhySO_log_mixed_mode, respectively.
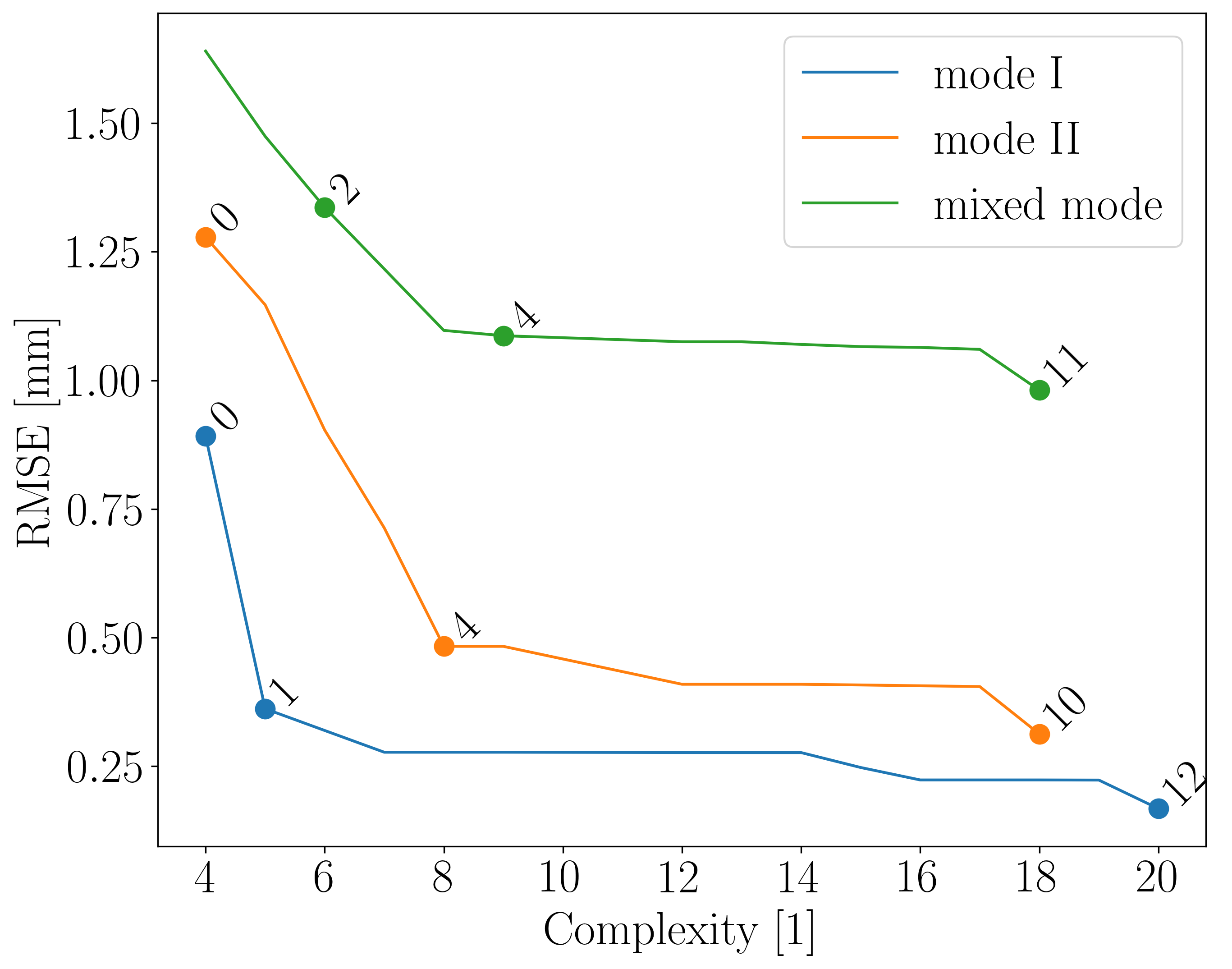
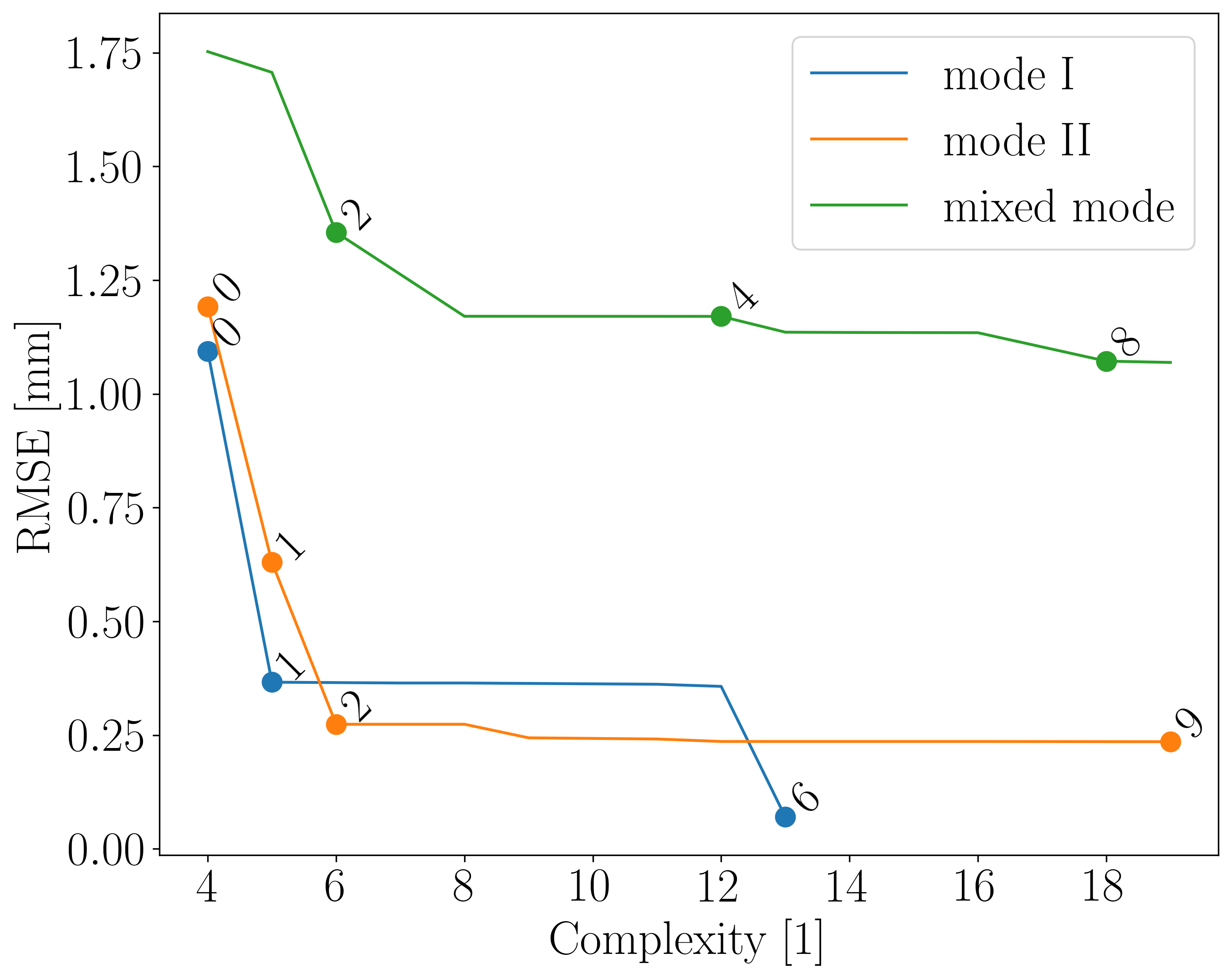
During training of the symbolic regression model, we obtain a set of formulas that trade off complexity and accuracy (RMSE).
We visualize these trade-offs using Pareto fronts. Running 06_Plot_pareto_fronts.py will separately generate the Pareto fronts for
the different trainings from the previous step.
To obtain the plots for the paper, we run the script 06_Pareto_Front_Plot_PhySO.py from folder scripts_paper.
 |
 |
|---|---|
| Pareto plot for the x-correction formulas | Pareto plot for the y-correction formulas |
| Mode | Formula id numbers | Result dx | Result dy |
|---|---|---|---|
| I | (0,0) | ||
| II | (0,0) | ||
| I / II | (2,2) |
We visualize the correction vector fields for the discovered formulas using the script 08_Plot_vector_fields.py.
We show the convergence for different load cases and formulas using the script 09_Convergence_study_FEA.py.
In order to have an initial crack tip estimation, we introduce a method we call line interception method (LIM). This method is based on fitting a hyperbolic tangent function to the y-displacement to find the crack path and thresholding the von Mises strain to find the crack tip.
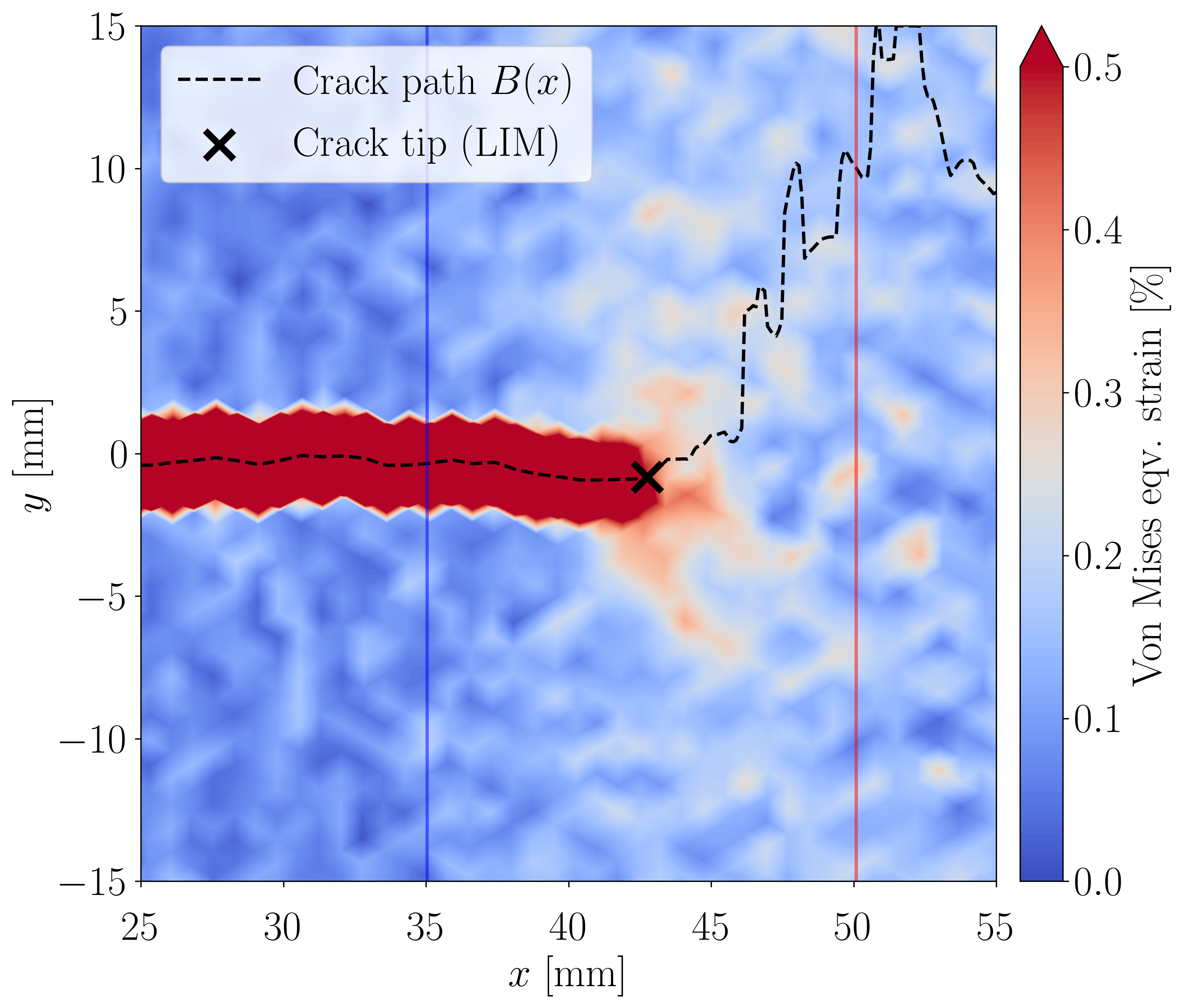 |
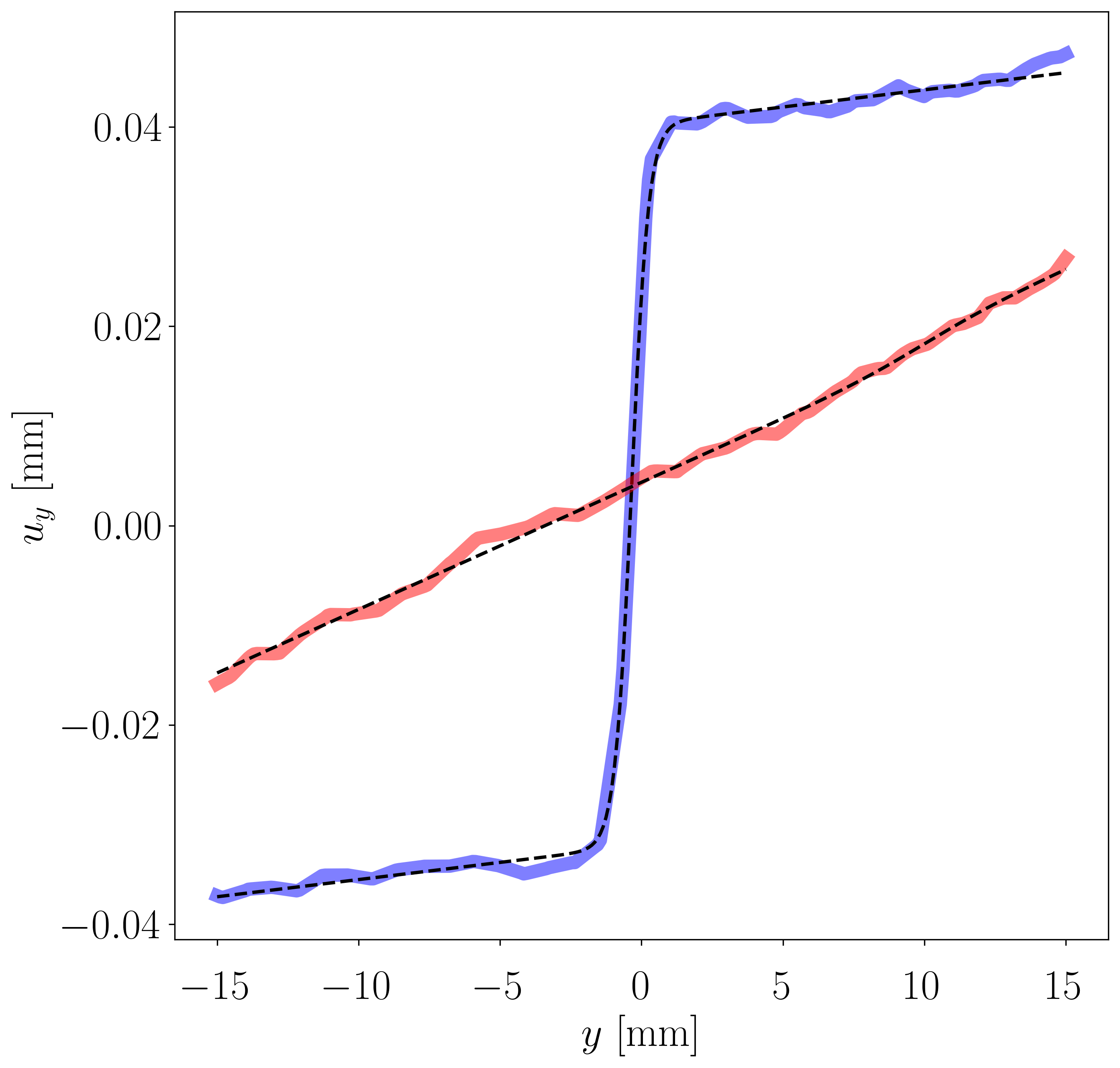 |
|---|---|
| Line interception method example | Fitted tanh functions |
We apply the discovered mode I formulas to experimental DIC data using the scripts in scripts_paper:
12a_Convergence_Mic_DIC_uniaxial.py12b_Convergence_Mic_DIC_biaxial.py13a_Application_DIC_uniaxial_pipeline.py13b_Application_Mic_DIC_uniaxial_pipeline.py13c_Application_DIC_biaxial_pipeline.py13d_Application_Mic_DIC_biaxial_pipeline.py
 |
 |
|---|---|
| Iterative correction for high-resolution DIC data of uniaxial test experiment | Convergence of |
We compare the stability over time of the corrected and the uncorrected crack tip positions using the script 14_da_dN_comparison.py.
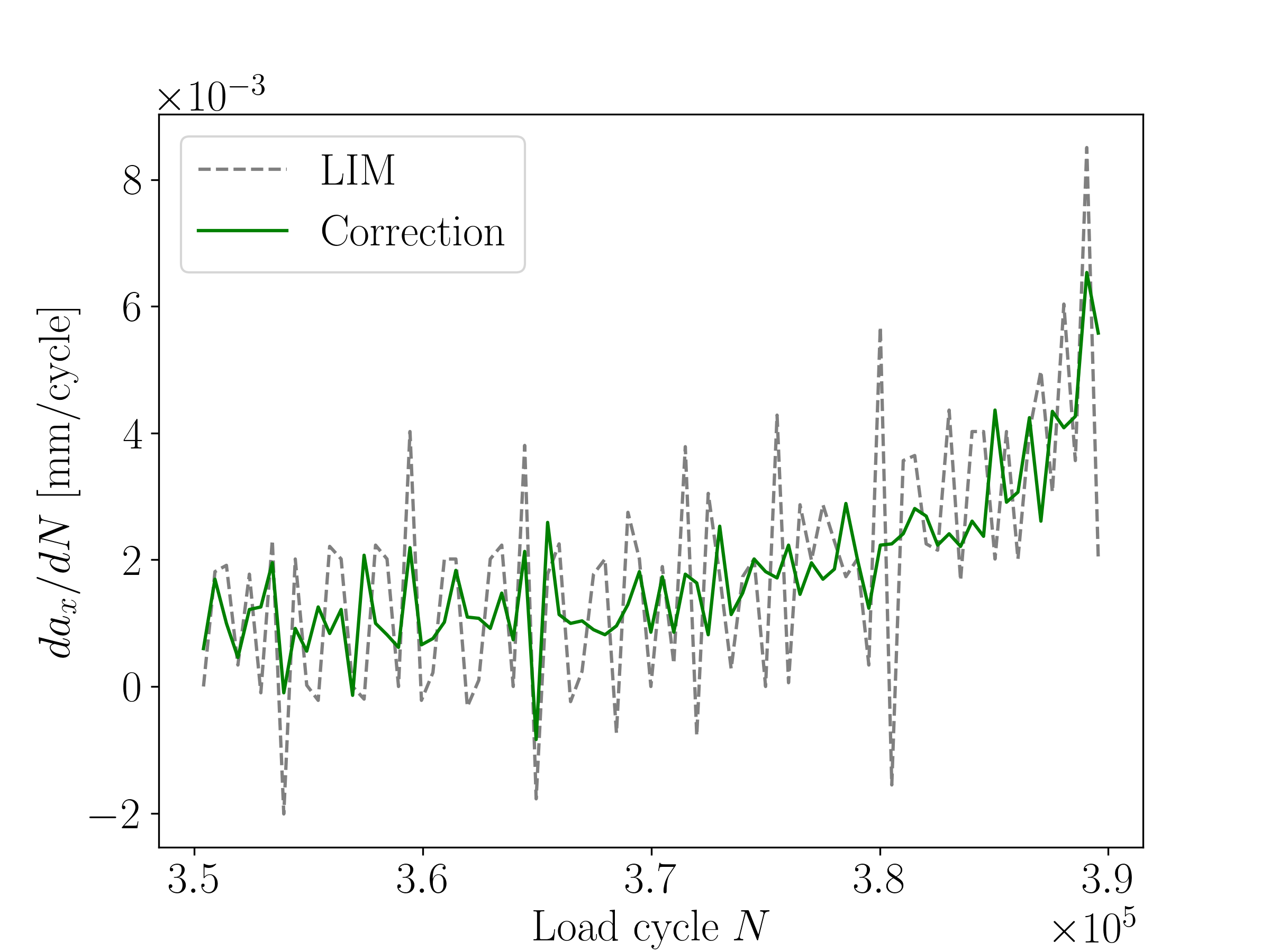 |
|---|
| Crack detection stability comparison of correction and line interception method |
This project is licensed under the MIT License - see the LICENSE file for details.