burnside-graphs
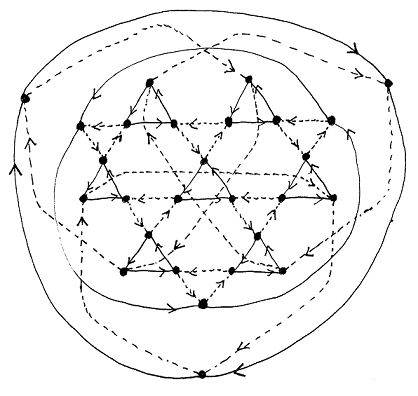
Image: a nice drawing of the 27-element group B(2,3)
A C++ program to compute the Cayley graph of 2-generator Burnside groups
The Burnside group B(m,n) is the largest group with m generators and exponent n. This program computes Cayley graphs of B(2,n) using a heuristic method that iteratively extends then prunes the graph.
New paths are added in such a way that relations of the form g^n = 1 are likely to cause pruning later on in the process, eventually resulting in a finite graph (which must be the Cayley graph).
The program successfully computes B(2,n) for n = 2, 3, and 4. It's unknown if B(2,5) is finite; if it is finite, it's too large to be computed in this way. Further, there is no guarantee that this program will be able to compute the graph, even given infinite time and memory.
How to build
You will need C++ compilation tools - I use mingw-w64 on Windows, using the g++ compiler:
- Install mingw-64 and add the executable to your PATH (see instructions here).
git cloneor download and unzip this repo- Go the downloaded project folder, open a command shell, and run:
g++ -g src\*.cpp -o main.exe
How to use
Note: The program computes the Cayley graph of B(2,3). To compute B(2,2) or B(2,4) you'll need to set n=2 or n=4 in the source code and rebuild main.exe (see instructions above).
Run main.exe. The program will prompt you to enter new identities - just skip this by typing "n". Once the graph is finished, the program will save graphinfo.txt and exit.
graphinfo.txt contains all the information needed to construct the Cayley graph:
- the distinct nodes (group elements)
- the edges labelled with the first generator x ("x-edges")
- the edges labelled with the second generator y ("y-edges")