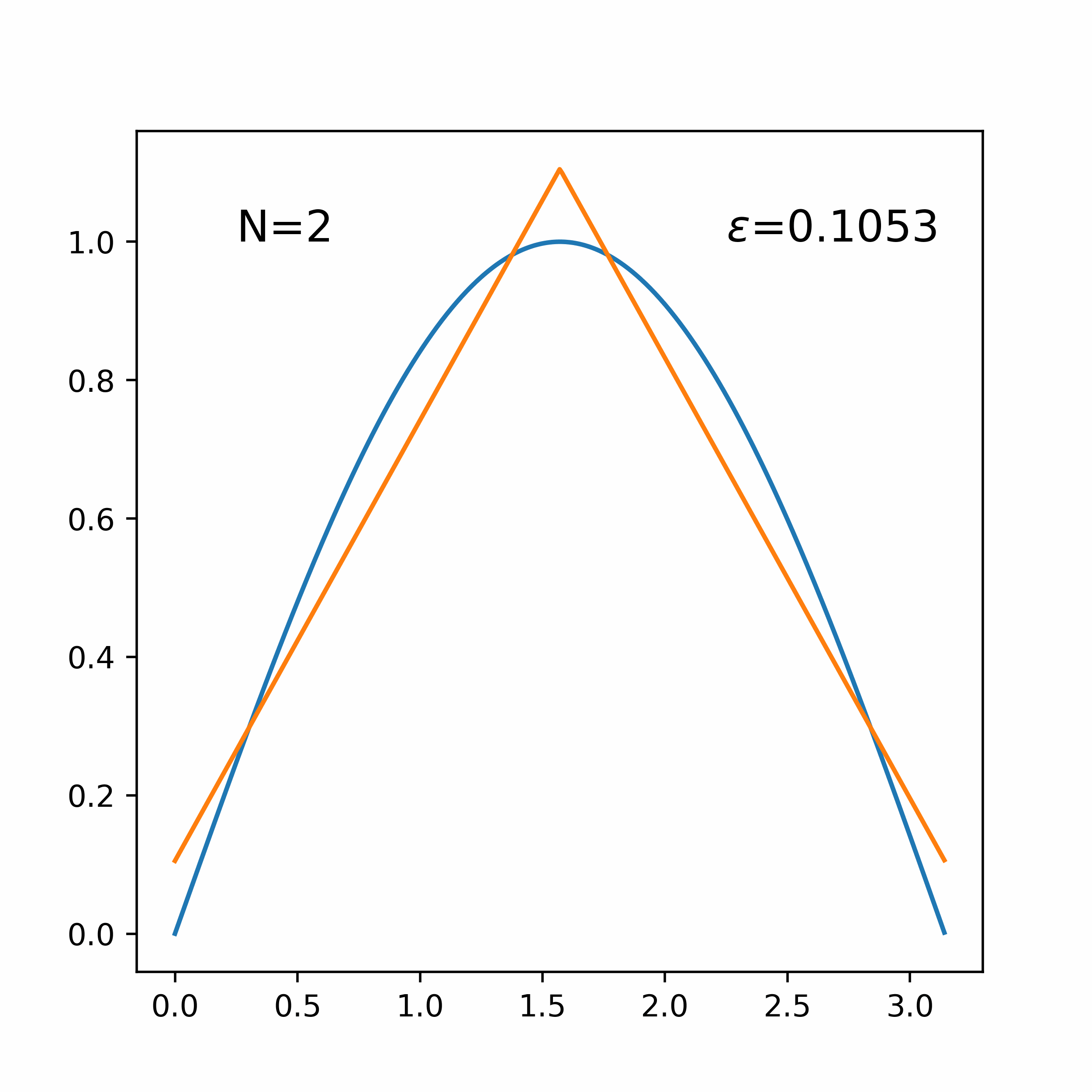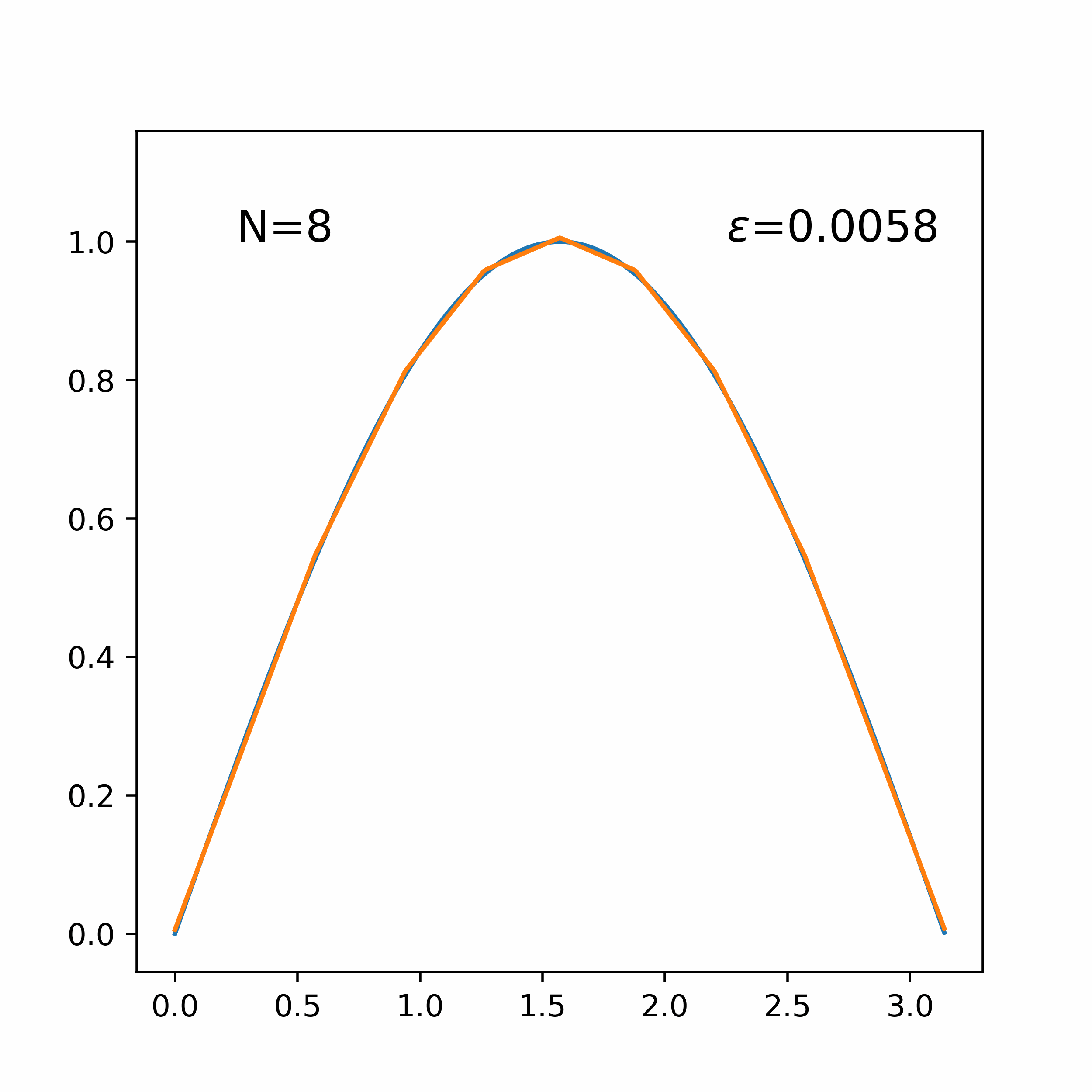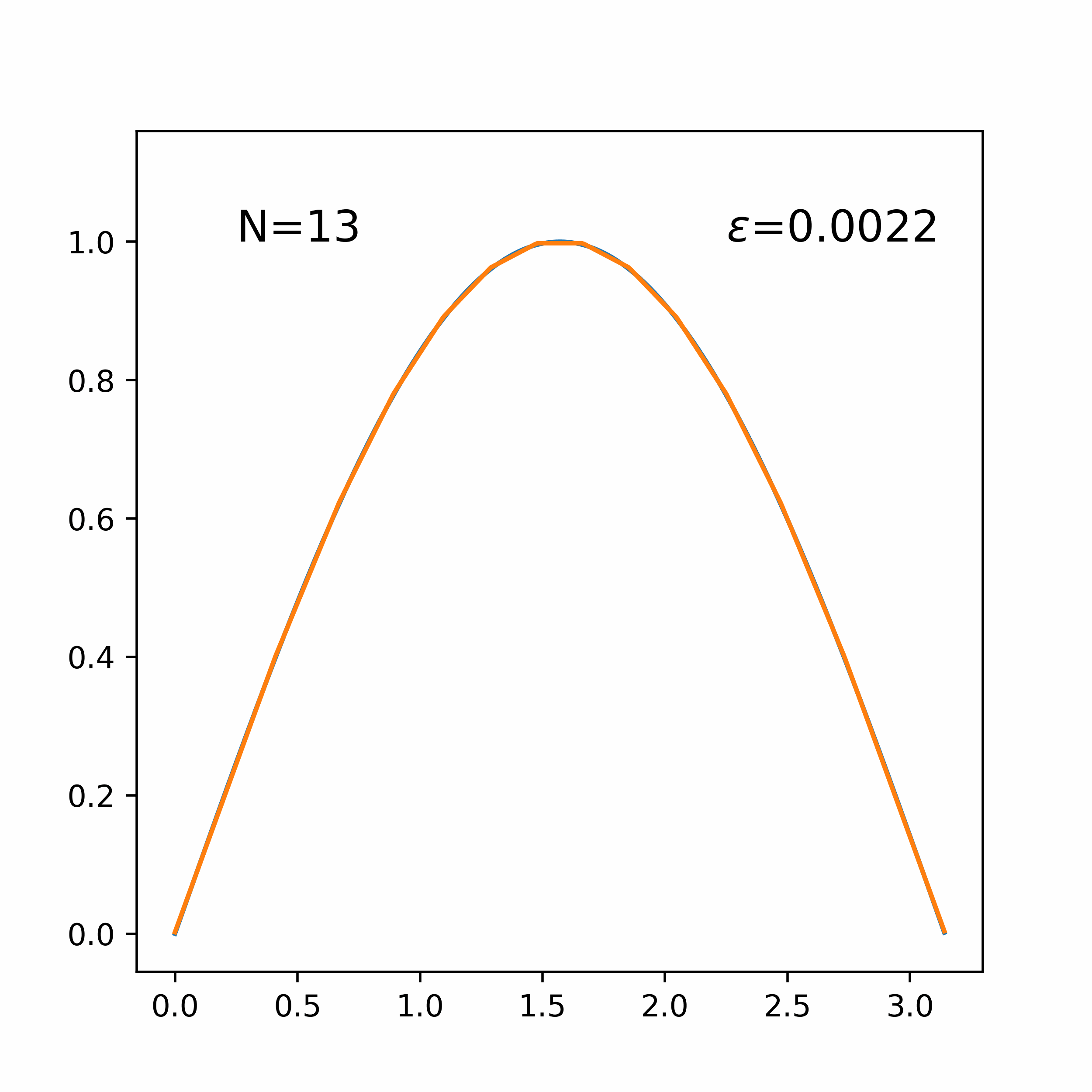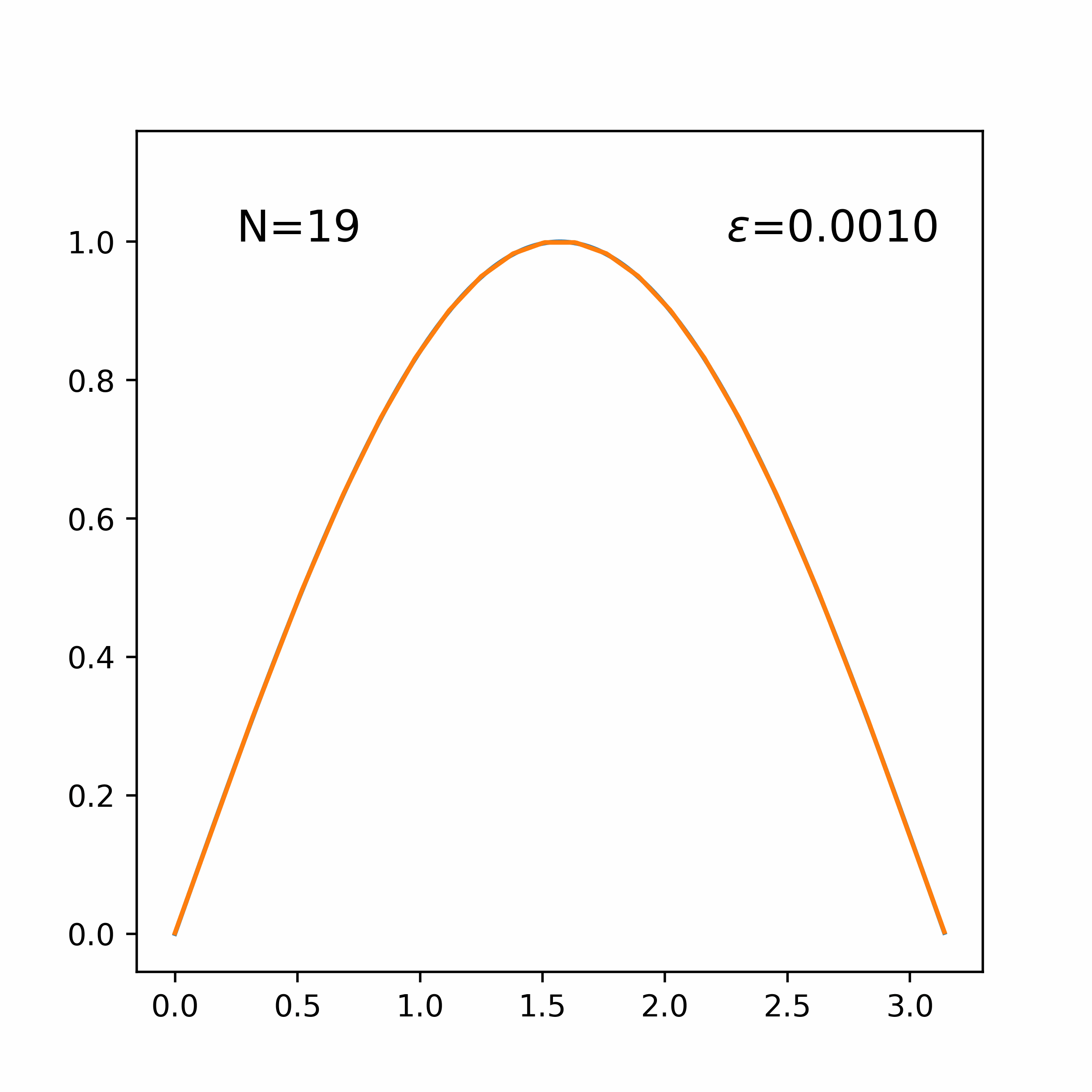
A python implementation of the algorithm used to generate optimal piecewise linear approximations of convex functions proposed by Imamoto and Tang [1]. The algorithm uses an iterative search to find the piecewise linear function g with smallest minimax deviation from f.
Piecewise fit to sin(x) on the bounds [0, π], increasing the number of piecewise segments.
Use generate_approximation to generate an N-piece piecewise linear function which approximates the function f which is convex on the domain α0 to αN.
| Args. | |
|---|---|
f |
float -> float function to be a approximated. |
df |
float -> float derivative of f. |
alpha_0 |
lower bound of approximated domain. |
alpha_N |
upper bound of approximated domain. |
N |
positive integer number of linear pieces in PW approximation. |
delta |
desired accuracy in the errors of the iterative algorithm. If None, it will be set to 1/1000th maximum error. |
convex |
set True if the function is convex (with positive second derivative). Set False if the function is negative convex (negative second derivative). |
set_m |
If a list, generate_approximation optimizes the approximation with the given slopes. If None, the standard algorithm varying slopes will be applied. |
generate_approximation returns a function object approximation of f. You can also access attributes of the function such as slopes, intercepts, endpoints, pivots, and minimax error.
>>>import math
>>>from math import sin, cos
>>>g = generate_approximation(sin, cos, 0, math.pi, 7, convex=False)
>>>g(.5) #call to function
0.4756625413936362
>>>g.m #slopes
[0.9360169203662899,...,-0.9360169203662904]
>>>g.c #intercepts
[0.007654081210491187,...,2.9482379618689714]
>>>g.alpha #segment endpoints,
[0,...,3.141592653589793]
>>>g.t #pivots
[0.3596589272900163,...,2.781933726299778]
>>>g.epsilon #minimax error
0.007654081210491187
[1] Imamoto, A., & Tang, B. (2008, October). Optimal piecewise linear approximation of convex functions. In Proceedings of the world congress on engineering and computer science (pp. 1191-1194).