Contextual Bandits

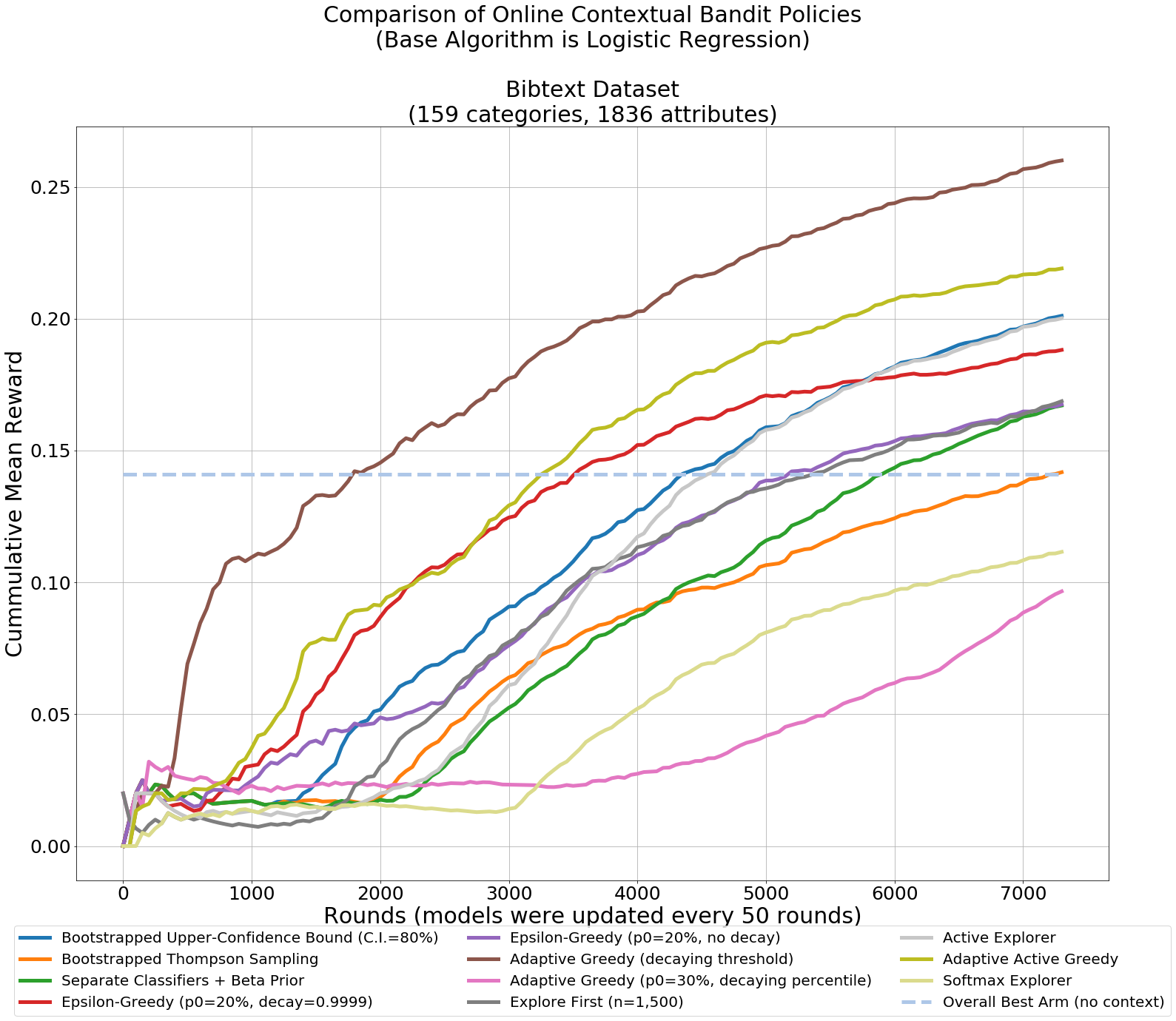
This Python package contains implementations of methods from different papers dealing with the contextual bandit problem, as well as adaptations from typical multi-armed bandits strategies. It aims to provide an easy way to prototype and compare ideas, to reproduce research papers that don't provide easily-available implementations of their proposed algorithms, and to serve as a guide in learning about contextual bandits.

The implementations of online algorithms are all described in the paper Adapting multi-armed bandits policies to contextual bandits scenarios: https://arxiv.org/abs/1811.04383

Paper can be cited as

@article{cortesbandits,
  title={Adapting multi-armed bandits policies to contextual bandits scenarios},
  author={Cortes, David},
  journal={arXiv preprint arXiv:1811.04383},
  year={2018}
}

Instalation

Package is available on PyPI, can be installed with

pip install contextualbandits

Problem description

Contextual bandits, also known as multi-armed bandits with covariates or associative reinforcement learning, is a problem similar to multi-armed bandits, but with the difference that side information or covariates are available at each iteration and can be used to select an arm, whose rewards are also dependent on the covariates.

The problem comes from an iterative process generating data as follows:

At each round, the world creates an observation consisting of a set of covariates (features) of fixed dimension, and a reward (which is stochastic but dependent on the covariates) for each arm/choice/label.
An agent must choose an arm or label for the observation.
The world reveals the reward for the arm chosen by the agent, but not for the other arms.

The aim is to create a policy that would maximize the rewards obtained by the agent. The arms might also expire over time and new arms might appear too, leading to the same exploration-exploitation dilemma faced in multi-armed bandits.

The problem is very similar to multi-class or multi-label classification (with the reward being whether the right label was chosen or not), but with the big difference that the right label or set of labels is not known for each observation, only whether the label that was chosen by the agent for each observation was correct or not.

Examples of such scenarios include online advertising, where we only know whether a user clicked an ad that he was presented with, but don't know which other ads he would have clicked; or clinic trials where we know how a person responded to a treatment, but don't know how he would have responded to a different treatment.

While, in general, algorithms for the contextual bandits problem assume continuous rewards in the range [0,1], this package deals only with the case of discrete rewards {0,1}, and only with the case of arms that all see the same covariates.

Three of the main problematics that arise in contextual bandits are:

Building a policy or strategy for making choices in an online setting that would manage exploration of new arms under different features, or exploitation of arms that are known to be good for some features – covered in contextualbandits.online.
Building a policy/algorithm with data collected from a different policy, covered in contextualbandits.offpolicy.
Evaluating the performance of different strategies/policies/algorithms based on partially-labeled data, covered in contextualbandits.evaluation.

This package does not deal with other related topics such as:

Incorporating social networks and similarity information between observations and/or arms – for some implementations of methods dealing with similarity information see BanditLib
Bandits with “expert advise” (e.g. Exp4, OnlineCover)
Online clustering (used for defining similarity buckets)

For more information, see the user guides below.

Most of the algorithms here are meta-heuristics that take a binary classifier (such as Logistic Regression or XGBoost) as a black-box oracle.

Getting started

You can find detailed usage examples with public datasets in the following IPython notebooks:

Documentation

Package documentation is available in readthedocs: http://contextual-bandits.readthedocs.io/en/latest/

Documentation is also internally available through docstrings (e.g. you can try help(contextualbandits.online.BootstrappedUCB), help(contextualbandits.online.BootstrappedUCB.fit), etc.).

Implemented algorithms

Implementations in this package include:

Online:

LinUCB (see [2] and [11])
Linear Thompson Sampling (see [4])

Adaptations from multi-armed bandits strategies:

Upper-confidence Bound (see [1], [6] and [3])
Thompson Sampling (see [1] and [3])
Epsilon Greedy (see [1], [7] and [6])
Adaptive Greedy (see [1] and [5])
Explore-Then-Exploit (see [1])

Other:

Exploration based on active learning (see [1])

Off-policy:

Offset Tree (see [8])
Doubly-Robust Policy Optimization (see [10])

Evaluation:

Rejection Sampling (see [2])
Doubly-Robust Policy Evaluation (see [9])

Some of the policies here such as AdaptiveGreedy haven't been yet evaluated or analyzed in any research papers for the scenario of contextual bandits though, and there might be better ways to convert the corresponding multi-armed bandits strategies to contextual bandits strategies than how it was done here.

Most of the methods here can work with streaming data by fitting them to the data in batches if the base classifier has a partial_fit method. They otherwise require to be refit to all the historic data every time they are updated. In batch training mode, methods based on bootstrapping approximate resamples either through setting random weights or through including each observation a number of times ~ Poisson(1) (see documentation for details).

Some comments

Many of the algorithms here oftentimes don't manage to beat simpler benchmarks (e.g. Offset Tree vs. a naïve One-Vs-Rest using only subsets of the data for each classifier), and I wouldn't recommend relying on them. They are nevertheless provided for comparison purposes.

This package assumes that the binary classification algorithms used have probabilistic outputs, ideally with a predict_proba method, or with a decision_function method to which it will apply a sigmoid transformation. Under some of the online algorithms or if using smoothing, this will not work very well with SVM and some forms of gradient boosting, in which case you'll need to programmatically define a new class that performs a recalibration within its fit method, and outputs the calibrated numbers through its predict_proba (see reference [12]).

Be aware that this is a research-oriented package and it has not been optimized for speed, nor does it use parallelism across arms.

References

[1] Cortes, D. (2018). Adapting multi-armed bandits policies to contextual bandits scenarios. arXiv preprint arXiv:1811.04383.

[2] Li, L., Chu, W., Langford, J., & Schapire, R. E. (2010, April). A contextual-bandit approach to personalized news article recommendation. In Proceedings of the 19th international conference on World wide web (pp. 661-670). ACM.

[3] Chapelle, O., & Li, L. (2011). An empirical evaluation of thompson sampling. In Advances in neural information processing systems (pp. 2249-2257).

[4] Agrawal, S., & Goyal, N. (2013, February). Thompson sampling for contextual bandits with linear payoffs. In International Conference on Machine Learning (pp. 127-135).

[5] Chakrabarti, D., Kumar, R., Radlinski, F., & Upfal, E. (2009). Mortal multi-armed bandits. In Advances in neural information processing systems (pp. 273-280).

[6] Vermorel, J., & Mohri, M. (2005, October). Multi-armed bandit algorithms and empirical evaluation. In European conference on machine learning (pp. 437-448). Springer, Berlin, Heidelberg.

[7] Yue, Y., Broder, J., Kleinberg, R., & Joachims, T. (2012). The k-armed dueling bandits problem. Journal of Computer and System Sciences, 78(5), 1538-1556.

[8] Beygelzimer, A., & Langford, J. (2009, June). The offset tree for learning with partial labels. In Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 129-138). ACM.

[9] Dudík, M., Langford, J., & Li, L. (2011). Doubly robust policy evaluation and learning. arXiv preprint arXiv:1103.4601.

[10] Dudík, M., Erhan, D., Langford, J., & Li, L. (2014). Doubly robust policy evaluation and optimization. Statistical Science, 485-511.

[11] Chu, W., Li, L., Reyzin, L., & Schapire, R. (2011, June). Contextual bandits with linear payoff functions. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (pp. 208-214).

[12] Kuhn, M., & Johnson, K. (2013). Applied predictive modeling (Vol. 26). New York: Springer.

dobriban/contextualbandits