Calculation of the cartesian coordinates from ellipsoidal:
Define ellipsoidal parameters first (e.g. semi-major axis a and eccentricity e). Then we select ellipsoidal parameters of an arbitary point latitude, longitude and h (high from the ground) and recalculate them to cartesan coordinates. The Geodetic Reference System 1980 (GRS 80) is used in this project. It is a geodetic reference system consisting of a global reference ellipsoid and a normal gravity model.
In this project I used coorinates of the Ankara/Turkey (phi1, lam1 and h1).
The data and information described in this repository are within the scope of the Advanced Geodesy and Geodetic Astronomy course. This course is given by Dr. hab. inż. Wojciech Jarmołowski. I learned a lot from him.
First, we need to build change.m function to calculate parameters and make transformation.
function demise = change(ddd);
dgr=fix(ddd);
min=fix((ddd-dgr)*60);
sec=((ddd-dgr)*60-min)*60;
demise=[dgr min sec]
%save('azymut.mat');
Now we have three cartesian coordinates (x, y, z) which can be iteratively recalculated back to three ellipsoidal parameters.
clc
a=6378137; % semi-major axis GRS80
f=1/298.257222101; % flattening GRS80
ekw=2*f-f^2; % first eccentricity GRS80
b = a*sqrt(1-ekw);
deg = pi / 180;
rad = 180 / pi;
Iterative formulas start from the h and approximation of geodetic latitude by geocentric latitude.
% as first approximation of ellipsoidal height - zero
phi=39 + 52/60 + 20.176/3600;
lam=32 + 45/60 + 42.451/3600;
phi1 = phi * deg;
lam1 = lam * deg;
h1 = 100;
N = a ./ sqrt(1 - ekw .* sin(phi1).^2);
x = (N + h1) .* cos(phi1) .* cos(lam1);
y = (N + h1) .* cos(phi1) .* sin(lam1);
z = ((1 - ekw) .* N + h1) .* sin(phi1);
We calculate iteratively radius of curvature in prime vertical (N) and 2 of 3 coordinates to convergencı(4-5 iterations).
p = sqrt(x.^2+y.^2);
firad(1) = atan(z/p); % as 1st approximation of geodetic latitude - geocentric
h(1) = 0;
for i=1:5
N(i) = a/sqrt(1-ekw*sin(firad(i))^2); % successive iterations of curvature radius N
h(i+1) = p/cos(firad(i))-N(i); % successive iterations of ellipsoidal height
firad(i+1) = atan((z/p)*(1-ekw*(N(i)/(N(i) + h(i+1))))^-1); % it. of geod. latitude
end
lastv = firad(end);
lastv1 = lastv * rad;
latitude = change(lastv1)
h1 = h(end)
longitude = change(lam)
Geodetic longitude (lambda) is calculated simply from arctan(y/x). We consider quaters of full angle and therefore it is convenient to use function azimuth from previous exercises.
figure
[xe, ye, ze] = ellipsoid(0,0,0,a,a,b,30); % function for drawing the ellipsoid
surf(xe, ye, ze);
hold on
plot3(x,y,z,'bo','MarkerSize',20,'MarkerFaceColor','g');
hold on
% yellow dot denotes zero meridian
plot3(a,0,0,'ro','MarkerSize',20,'MarkerFaceColor','y');
hold off
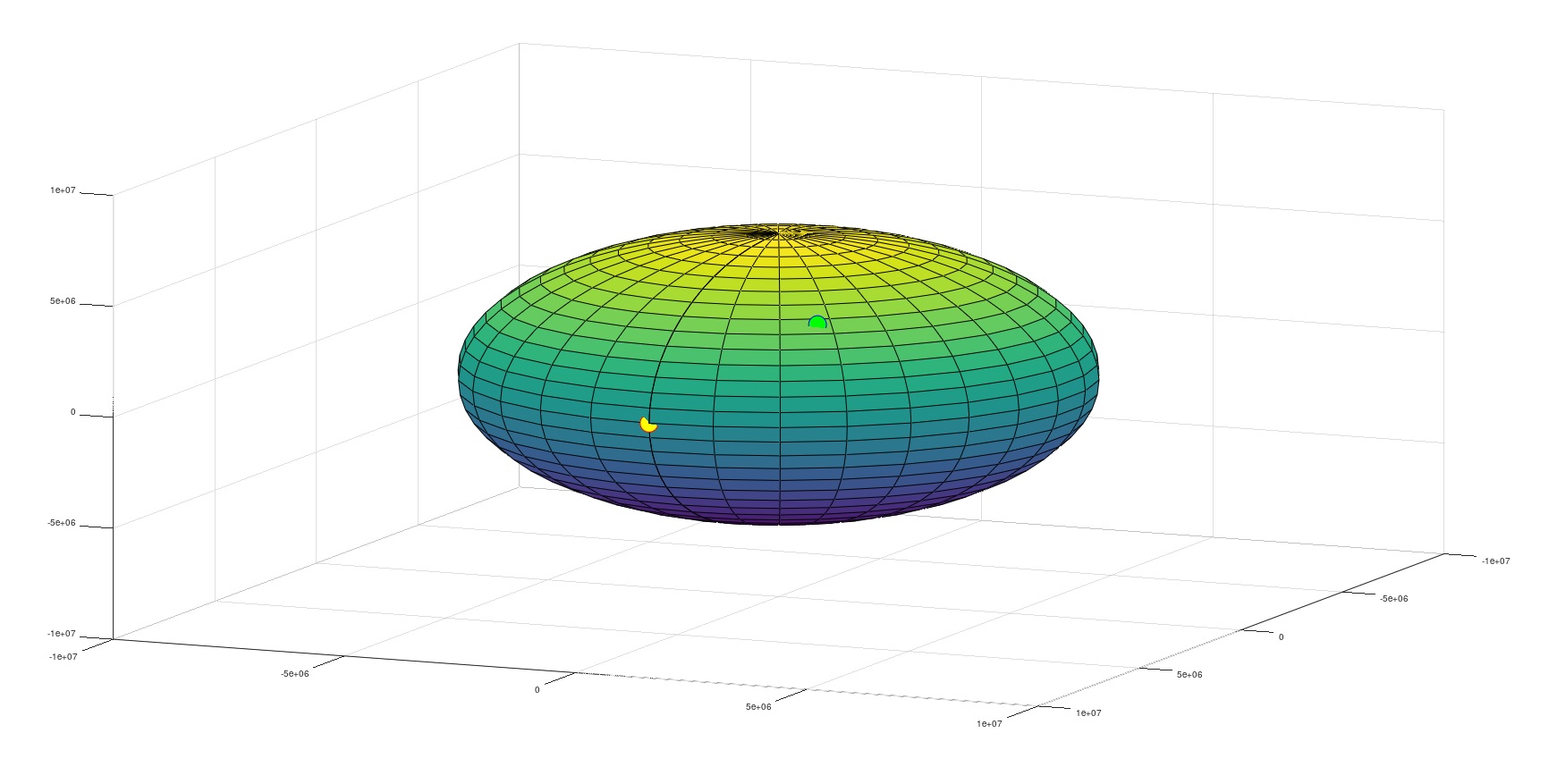
As we can see from the plot, yellow point is the intersection of the greenwich and equator. Green point is showing the position of Ankara. In command window we can see the results which is coordinates of the Ankara.
Coordinates are saved via fopen at the end of the project as .txt file named ofile.
fid = fopen('ofile.txt','w');
fprintf(fid,'%14.8f %14.8f %10.3f\n', [phi1, lam1, h1]');
fclose('all');
If you have something to say to me please contact me:
- Twitter: Doguilmak
- Mail address: doguilmak@gmail.com