fn

Function approximation with Neural Networks!

Using shallow neural networks to learn mathematical functions. Trigonometric functions, rational functions, polynomials, etc etc Even boolean functions! (build a small CPU with neural networks as the logical gates?)

This is currently intended to function like sklearn's MLPRegressor object.

Example, learning sin(x) on [-5, 5)

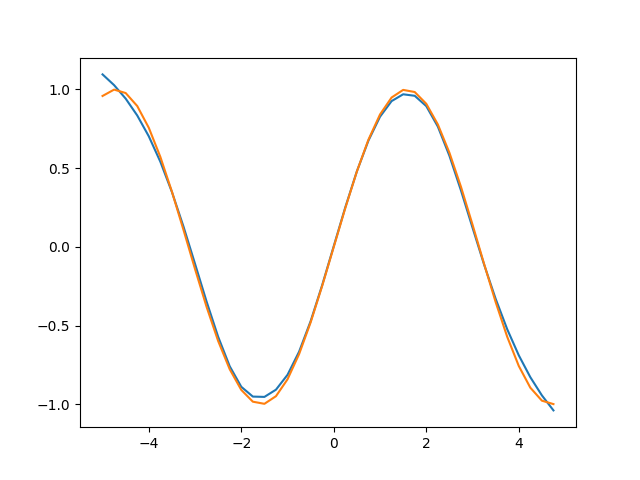
import numpy as np
from fn import Fn

f = np.sin
X = np.arange(-5, 5, 0.25)
model = Fn(sizes=[1, 1096, 1096, 1096, 1], activations=['tanh', 'tanh', 'tanh'], loss='l1', optimizer="adam")
model.fit(X, f, epochs=750)

@np.vectorize
def model_(x):
    return model(torch.Tensor([x]).to(model.device)).detach().cpu()
    
y = model_(X)
plt.plot(X, y)
plt.plot(X, f(X))

plt.show()

the model will look like

A trained model can easily be used as a function

from math import pi
import numpy as np
from fn import Fn

f = np.sin
X = np.arange(0, 2*pi + 1, 0.25)

model = Fn(sizes=[1, 1096, 1096, 1096, 1], activations=['tanh', 'tanh', 'tanh'], loss='l1', optimizer="adam")
# Fit the model on sin(x) over the interval [0, 2pi]
model.fit(X, f, epochs=250)

# using our model to compute sin(0)
y = model(0.0).item()
print(y)

Visualizing model architecture

The Fn object's str method uses the torchsummary library to return a Keras-like summary of the model

model = Fn(sizes=[1, 1096, 1096, 1], activations=['tanh', 'tanh', 'tanh'], loss='l2')
print(model)

>>> 
=================================================================
Layer (type:depth-idx)                   Param #
=================================================================
├─Linear: 1-1                            2,192
├─Tanh: 1-2                              --
├─Linear: 1-3                            1,202,312
├─Tanh: 1-4                              --
├─Linear: 1-5                            1,097
├─Tanh: 1-6                              --
=================================================================
Total params: 1,205,601
Trainable params: 1,205,601
Non-trainable params: 0
=================================================================

Theory

The Universal Approximation Theorem states that a neural network with a single hidden layer can approximate any continious function on a closed interval to arbitrary error

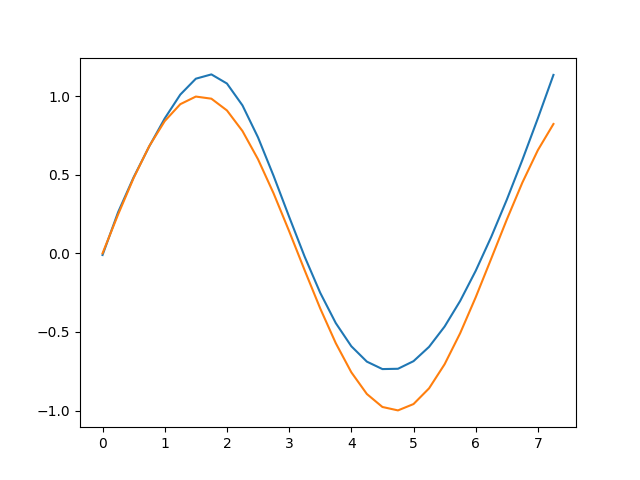
An extreme example,

Learning sin(x) on [0, 2π] with a single hidden layer (500k neurons)

from math import pi
import numpy as np
from fn import Fn

f = np.sin
X = np.arange(0, 2*pi + 1, 0.25)

model = Fn(sizes=[1, 500_000, 1], activations=['tanh'], loss='l2')
model.fit(X, f, epochs=500)

@np.vectorize
def model_(x):
    return model(torch.Tensor([x]).to(model.device)).detach().cpu()

y = model_(X)

plt.plot(X, y)
plt.plot(X, f(X))

plt.show()

not bad for 1 hidden layer.

domsalva/fn

fn

Example, learning sin(x) on [-5, 5)

Visualizing model architecture

Theory

Learning sin(x) on [0, 2π] with a single hidden layer (500k neurons)