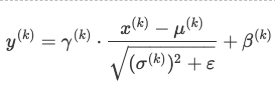-
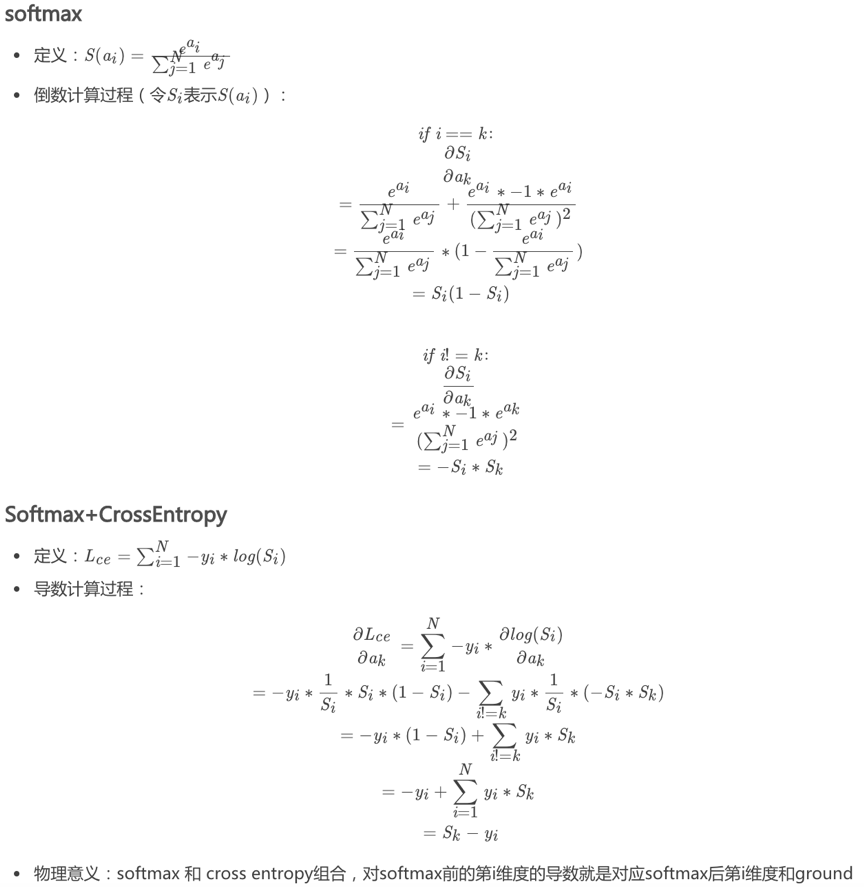
作用:
- 使得每层的输入/输出分布更加稳定,避免参数更新和网络层次变深大幅度影响数据分布。从而使模型训练更稳定。
-
参数 β 和 γ的作用
- 保留网络各层在训练过程中的学习成果
- 保证激活单元的非线性表达能力
- 使批归一化模块具有复原初始输出分布能力。
-
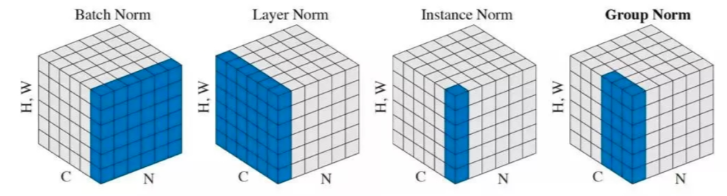
BN放在激活层之前还是之后
在inference阶段,可以将BN层的参数合并在之前的Linear或Conv层中,加速推断时间(因为二者都是线性变换)。
w = module.weight.data
b = module.bias.data # conv的bias可以用全0代替
ws = [1] * len(w.size())
ws[0] = w.size()[0]
invstd = bn_module.running_var.clone().add_(bn_module.eps).pow_(-0.5)
w.mul_(invstd.view(*ws).expand_as(w))
b.add_(-bn_module.running_mean).mul_(invstd)
if bn_module.affine:
w.mul_(bn_module.weight.data.view(*ws).expand_as(w))
b.mul_(bn_module.weight.data).add_(bn_module.bias.data)- 采用Focal Loss或OHEM进行负样本挖掘,加大Hard Example损失权重
- 训练时只利用Ground Truth周边的Prior Boxes进行训练,忽略其他背景区域,只考虑困难背景区域
- ROIPool存在两次量化误差,首先是将候选框边界量化为整数点坐标值,其次是将量化后的边界区域平均分割成 k x k 个单元,对每一个单元的边界进行量化。ROIAlign通过双线性插值避免了量化操作,保存了原始ROI的空间分布,有效避免了误差的产生;对于检测图片中大目标物体时,两种方案的差别不大,而如果是图片中有较多小目标物体需要检测,则优先选择ROIAlign,更精准一些
首先要求解两个多边形的面积,方法见该链接
关键在于如何求出交集的面积
思路一
蒙特卡洛 + 采样,近似求解交集的面积,但是中间涉及判断点在不在多边形内,判断点是否在多边形内
思路二
适合于两个凸多边形(非凸没想到好的思路),凸多边形可以看做是半平面的交集,因此两个凸多边形的交集,可以看作是(m+n)个半平面的交集(假设两个凸多边形分别有m个顶点和n个顶点),求出来半平面的交集(仍旧是一个凸多边形)之后,求解该多边形的面积即可。求解半平面交集
- 在训练时,我们可以计算出batch的均值和方差,迭代训练过程中,均值和方差一直在发生变化。但是在推理时,均值和方差是固定的,对于均值来说直接计算所有batch u值的平均值,对于标准偏差采用每个batch σB的无偏估计。