This repository contains a PyTorch implementation of a demonstrative example in the following paper:
- Zhilu Lai, Wei Liu, Xudong Jian, Kiran Bacsa, Limin Sun, and Eleni Chatzi. Neural modal ordinary differential equations: Integrating physics-based modeling with neural ordinary differential equations for modeling high-dimensional monitored structures. Data-Centric Engineering, Volume 3, 2022, e34.
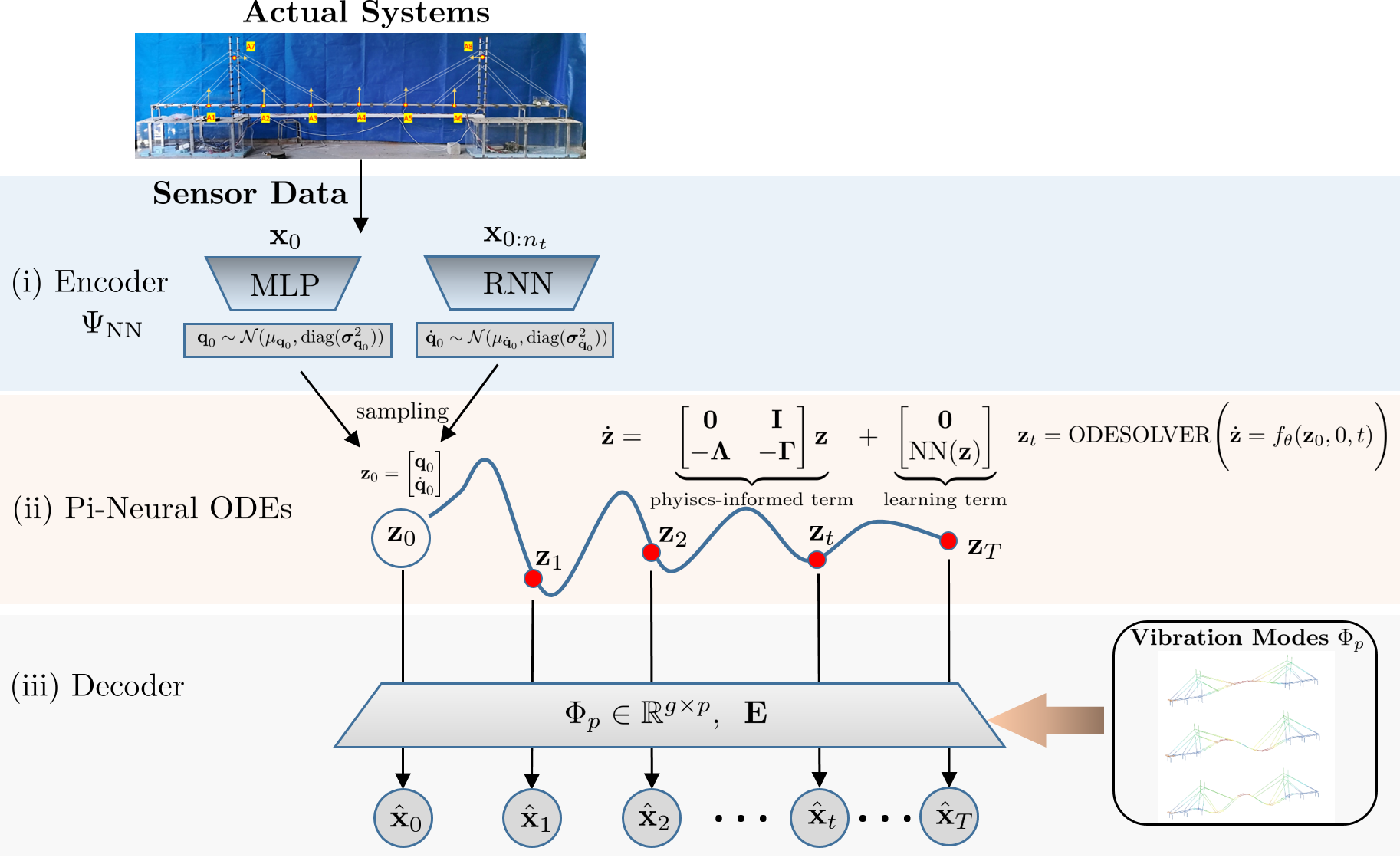
The architecture of Neural Modal ODEs is comprised of:
- an encoder
$\Psi_{\text{NN}}$ : performing inference from a handful observational data to the initial conditions of latent quantities$\textbf{z}_0$ - Physics-informed Neural ODEs (Pi-Neural ODEs): modeling the dynamics of latent quantities structured by a modal representation added by a learning term
- a decoder
$\Phi_p$ : emitting the latent quantities to the full-field observational space, enforced by the eigenmodes derived from eigenanalysis of the structural matrices of the (or linearized) physics-based models
In this 4-DOF nonlinear Structural Dynamical System, we only measure
-
The full-field responses are successfully reconstructed via Neural Modal ODEs.
-
"FEM" in the figure, means the purely physics-based model, where we intentionally introduce model noise into the model. We integrate this "inaccurate" model with observational data via Neural Model ODEs, forming a hybrid model -- the learning term
$\text{NN}(\textbf{z})$ parametrized by a feed-forward neural network is capable of rectifying the model inaccuracy/discrepancy.
-
Neural_Modal_ODE_demo.py- main function, managing model training and testing. -
data_generation.py- function for generating data set from a simulated 4-DOF nonlinear system. -
models.py- PyTorch modules for the encoder. -
data- generated data set from a simulated dynamical system. -
modal_para.npz- modal parameters of the simulated system. -
measured_data_nonlinear.npz- generated observational data.