Mimas' Effect on Saturn's Cassini Ring Gap

Vincent Andrade
Adham Abdelwahab
Tyler Kaminski

Professor Lukic

PEP 351

I pledge my honor that I have abided by the Stevens Honor System.

Introduction

Equations

$\frac{GM}{4\pi^2} = \frac{d^3}{T^2}$

$\omega = \frac{2\pi}{T^2} \implies w = \sqrt{\frac{GM}{d^3}}$

$x_m = d\cos(\omega t)$

$y_m = d\sin(\omega t)$

$r_s = \sqrt{x(t)^2 + y(t)^2}$

$r_m = \sqrt{(x - x_m)^2 + (y - y_m)^2}$

$a_x(t) = \frac{-GM}{r_s^3} x(t) - \frac{Gm}{r_m^3} (x(t) - x_m(t))$

$a_y(t) = \frac{-GM}{r_s^3} y(t) - \frac{Gm}{r_m^3} (y(t) - y_m(t))$

$x(t + \Delta t) = x(t) + v_x(t)\Delta t + \frac{a_x (t) \Delta t^2}{2}$

$y(t + \Delta t) = y(t) + v_y(t)\Delta t + \frac{a_y (t) \Delta t^2}{2}$

$v_x(t + \Delta t) = v_x(t) + a_x(t)\Delta t$

$v_y(t + \Delta t) = v_y(t) + a_y(t)\Delta t$

$v_0 = \sqrt{\frac{GM}{r_s}}$

$v_x = -v_0 \sin(\theta)$

$v_y = -v_0 \cos(\theta)$

Assumptions

$x(t = 0) = r_s$

$y(t = 0) = 0$

$v_x(t = 0) = 0$

$v_y(t = 0) = v_0$

Saturn is at the origin (0,0).
Particles are initially evenly distributed along the x-axis between a lower and upper limit.
The lower and upper limits contain the Cassini Division.
Mass of Mimas is boosted in order to accelerate results.
Position of particles and Mimas are calculated for 60 and 1 second time steps.
Particles are massless and not affected by each other, only by Saturn and Mimas.

Constants

Gravitational Constant, $G = 6.6743 \times 10^{-11}$

Mass of Saturn, $M = 5.6834 \times 10^{26} kg$

Mass of Mimas, $m = 3.7493 \times 10^{19} kg$

Distance between Saturn and Mimas, $d = 1.8552 \times 10^8 m$

Cassini Division Inner Bound, $d_1 = 1.1758 \times 10^8 m$

Cassini Division Outer Bound, $d_2 = 1.2217 \times 10^8 m$

Python Implementation

import matplotlib.pyplot as plot
import numpy as np

# Constants for calculations
G = 6.67430e-11
# Mass of the central body (Saturn)
M = 5.6834e26
# Mass of Mimas
m = 3.7493e19
# Distance from Saturn to Mimas
d = 1.8552e8
# time step (1 minute)
t = 60


def orbit(interactive, num_particles, show_all, mimas_multiplier,
          num_time_steps):
    """
    Plot the orbit of Mimas and massless ring particles around Saturn.

    Parameters:
    interactive (bool): Plot the orbits in real time.
    num_particles (int): The number of particles to simulate.
    show_all (bool): Don't clear the plot between iterations.
    mimas_multiplier (int): Multipler of Mimas' mass.
    num_time_steps (int): The number of time steps to simulate.
    """
    # Entire range of Saturn's rings
    INNER_LIM = 74500 * 10**3
    OUTER_LIM = 140220 * 10**3
    # Range around the Cassini Division including B and A rings.
    # INNER_LIM = 92000 * 10**3
    # OUTER_LIM = 136780 * 10**3

    # particles = np.random.randint(-OUTER_LIM, OUTER_LIM, (num_particles, 2))
    p = np.array([(float(i), 0.0) for i in range(
        INNER_LIM, OUTER_LIM, (OUTER_LIM - INNER_LIM) // num_particles)])
    v = np.array([(0.0, np.sqrt(G * M / x)) for x, _ in p])

    plot.gca().set_aspect('equal')

    # omega used for calculating position of mimas
    w = np.sqrt(G * M / d**3)
    for n in range(0, num_time_steps * t, t):
        if not show_all:
            plot.cla()
        xm = d * np.cos(n * w)
        ym = d * np.sin(n * w)
        # Plot Saturn and Mimas
        if interactive or show_all or n == (num_time_steps - 1) * t:
            plot.plot(xm, ym, 'ro')
            plot.plot(0, 0, "yo")
        for i in range(len(p)):
            rs = np.sqrt(p[i][0]**2 + p[i][1]**2)
            rm = np.sqrt((p[i][0] - xm)**2 + (p[i][1] - ym)**2)
            ax = -G * M * p[i][0] / rs**3 - \
                G * m * mimas_multiplier * (p[i][0] - xm) / rm**3
            ay = -G * M * p[i][1] / rs**3 - \
                G * m * mimas_multiplier * (p[i][1] - ym) / rm**3
            p[i][0] += v[i][0] * t + ax/2 * t**2
            p[i][1] += v[i][1] * t + ay/2 * t**2
            v[i][0] += ax * t
            v[i][1] += ay * t
            if interactive or show_all or n == (num_time_steps - 1) * t:
                plot.plot(p[i][0], p[i][1], "go", markersize=1)
        if interactive:
            plot.pause(0.00000001)
    if not interactive:
        plot.savefig('img/mimas_mult=' + str(mimas_multiplier) + '&p=' +
                     str(num_particles) + '&t=' + str(num_time_steps) + '.png')
        print('Image Saved')


orbit(interactive=False, num_particles=1000, show_all=False,
      mimas_multiplier=10000, num_time_steps=2000)

C Implementation With Python Driver

#include <math.h>
#include <stdlib.h>
#include <stdio.h>

// Constants for calculations
float G = 6.67430e-11;
// Mass of the central body (Saturn)
float M = 5.6834e26;
// Mass of Mimas
float m = 3.7493e19;
// Distance from Saturn to Mimas
float d = 1.8552e8;
// time step (1 second)
int t = 1;

// Plot the orbit of Mimas and massless ring particles around Saturn.
// Parameters:
// num_particles: The number of particles to simulate.
// mimas_multiplier: Multiplier of Mimas' mass.
// num_time_steps: The number of time steps to simulate.
void orbit(int num_particles, int mimas_multiplier, int num_time_steps)
{
	// Range of entirety of Saturn's rings.
	// int INNER_LIM = 74500 * pow(10, 3);
	// int OUTER_LIM = 140220 * pow(10, 3);
	// Range around the Cassini Division including B and A rings.
	int INNER_LIM = 92000 * pow(10, 3);
	int OUTER_LIM = 136780 * pow(10, 3);
	// Range of only the Cassini Division.
	// int INNER_LIM = 117580 * pow(10, 3);
	// int OUTER_LIM = 122170 * pow(10, 3);

	float p[num_particles][2];
	float v[num_particles][2];
	for (int i = 0, j = INNER_LIM; j < OUTER_LIM;
	     j += (OUTER_LIM - INNER_LIM) / num_particles, ++i) {
		p[i][0] = j;
		p[i][1] = 0.0;
		v[i][0] = 0.0;
		v[i][1] = sqrt(G * M / p[i][0]);
	}
	// omega used for calculating position of mimas
	float w = sqrt(G * M / pow(d, 3));
	float xm = 0, ym = 0;
	for (int n = 0; n < num_time_steps * t; n += t) {
		xm = d * cos(n * w);
		ym = d * sin(n * w);
		for (int i = 0; i < num_particles; ++i) {
			float rs = sqrt(pow(p[i][0], 2) + pow(p[i][1], 2));
			float rm = sqrt(pow(p[i][0] - xm, 2) +
					pow(p[i][1] - ym, 2));
			float ax = -G * M * p[i][0] / pow(rs, 3) -
				   G * m * mimas_multiplier * (p[i][0] - xm) /
					   pow(rm, 3);
			float ay = -G * M * p[i][1] / pow(rs, 3) -
				   G * m * mimas_multiplier * (p[i][1] - ym) /
					   pow(rm, 3);
			p[i][0] += v[i][0] * t + ax / 2 * pow(t, 2);
			p[i][1] += v[i][1] * t + ay / 2 * pow(t, 2);
			v[i][0] += ax * t;
			v[i][1] += ay * t;
		}
	}
	printf("%f, %f\n", xm, ym);
	for (int i = 0; i < num_particles; ++i)
		printf("%f, %f\n", p[i][0], p[i][1]);
}

int main(int argc, char **argv)
{
	orbit(atoi(argv[1]), atoi(argv[2]), atoi(argv[3]));
	return 0;
}

import matplotlib.pyplot as plot
import csv
import subprocess
import sys
import numpy as np

if len(sys.argv) != 4:
    print("Usage:", sys.argv[0],
          "<num_particles> <mimas_multiplier> <num_time_steps>")
    exit(1)
subprocess.run(
    "clang -lm -fsanitize=safe-stack -Ofast -march=native sim_ring_gaps.c -o sim_ring_gaps",
    shell=True, check=True)
data_filename = 'data/mimas_mult=' + sys.argv[2] + '&p=' + sys.argv[1] + \
    '&t=' + sys.argv[3] + '.csv'
subprocess.run(
    "./sim_ring_gaps " + ' '.join(sys.argv[1:]) + " > '" + data_filename + "'",
    check=True, shell=True)
data = csv.reader(open(data_filename))
xm, ym = next(data)
plot.gca().set_aspect('equal')
plot.title("p=" + sys.argv[1] + ", m=" + sys.argv[2] +
           ", t=" + sys.argv[3])
plot.xlabel("Distance from Saturn (m)")
plot.ylabel("Distance from Saturn (m)")
plot.plot(float(xm), float(ym), "ro", label="Mimas")
plot.plot(0, 0, "yo", markersize=20, label="Saturn")
x, y = next(data)
plot.plot(float(x), float(y), "go", markersize=1, label="Ring Particle")
plot.legend(loc='upper right')

particles_in_division = 0.0
for x, y in data:
    if 1.1758e8 < np.sqrt(float(x)**2 + float(y)**2) < 1.2217e8:
        particles_in_division += 1
    plot.plot(float(x), float(y), "go", markersize=1)
print("Ratio of particles in division to total:",
      particles_in_division / int(sys.argv[1]))

plot.savefig('img/mimas_mult=' + sys.argv[2] + '&p=' + sys.argv[1] + '&t=' +
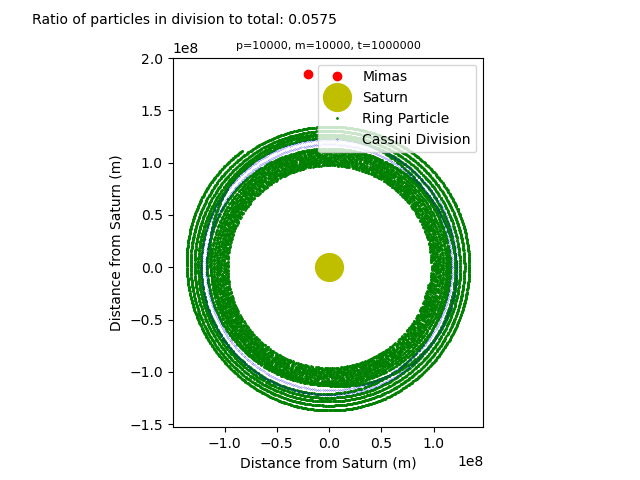
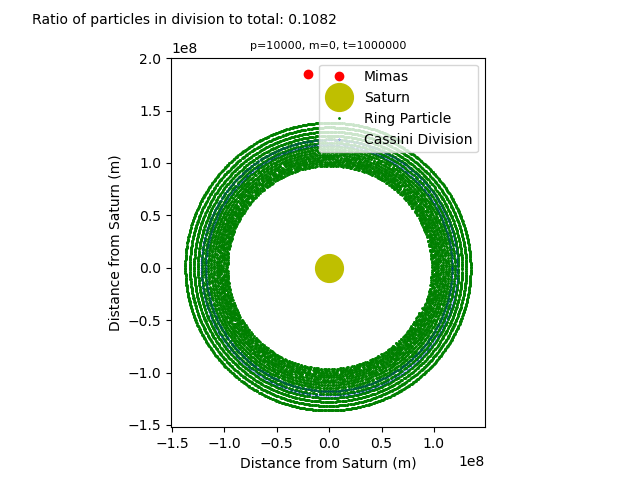
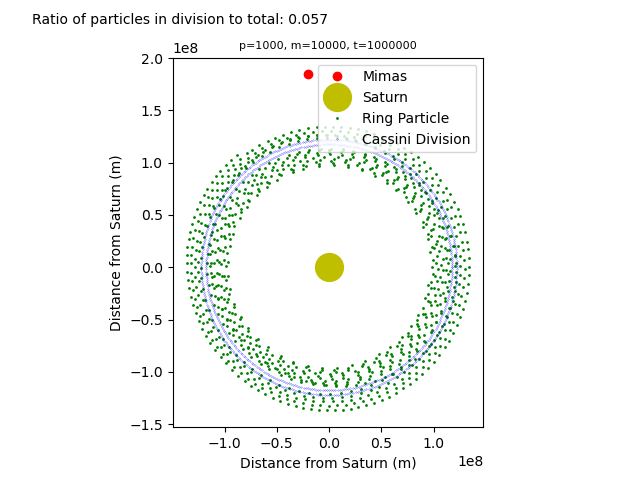
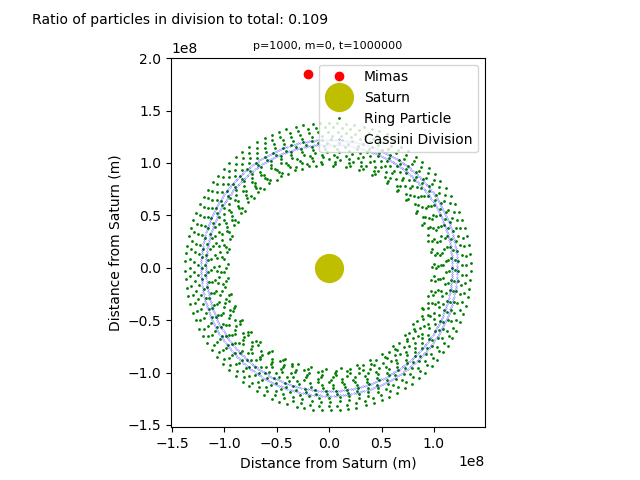
             sys.argv[3] + '.png')

Results

{width=50%} {width=50%}

Conclusions

With the introduction of Mimas, the orbits of the particles become unstable, with gaps and perturbations occurring throughout the rings. As seen in project 1, the Euler method is not the most accurate method for simulating orbital motion. The particles end up further away from their initial orbits that intended, even without Mimas’ gravity. Can be partially accounted for by drastically lowering time step at the cost of greater computation time required for simulating longer orbital periods. Differences between the orbits with and without Mimas’ gravity are very clear. Given enough particles and enough time steps, Mimas’ gravitational pull results in the Cassini division.

durcor/ring-gap-sim