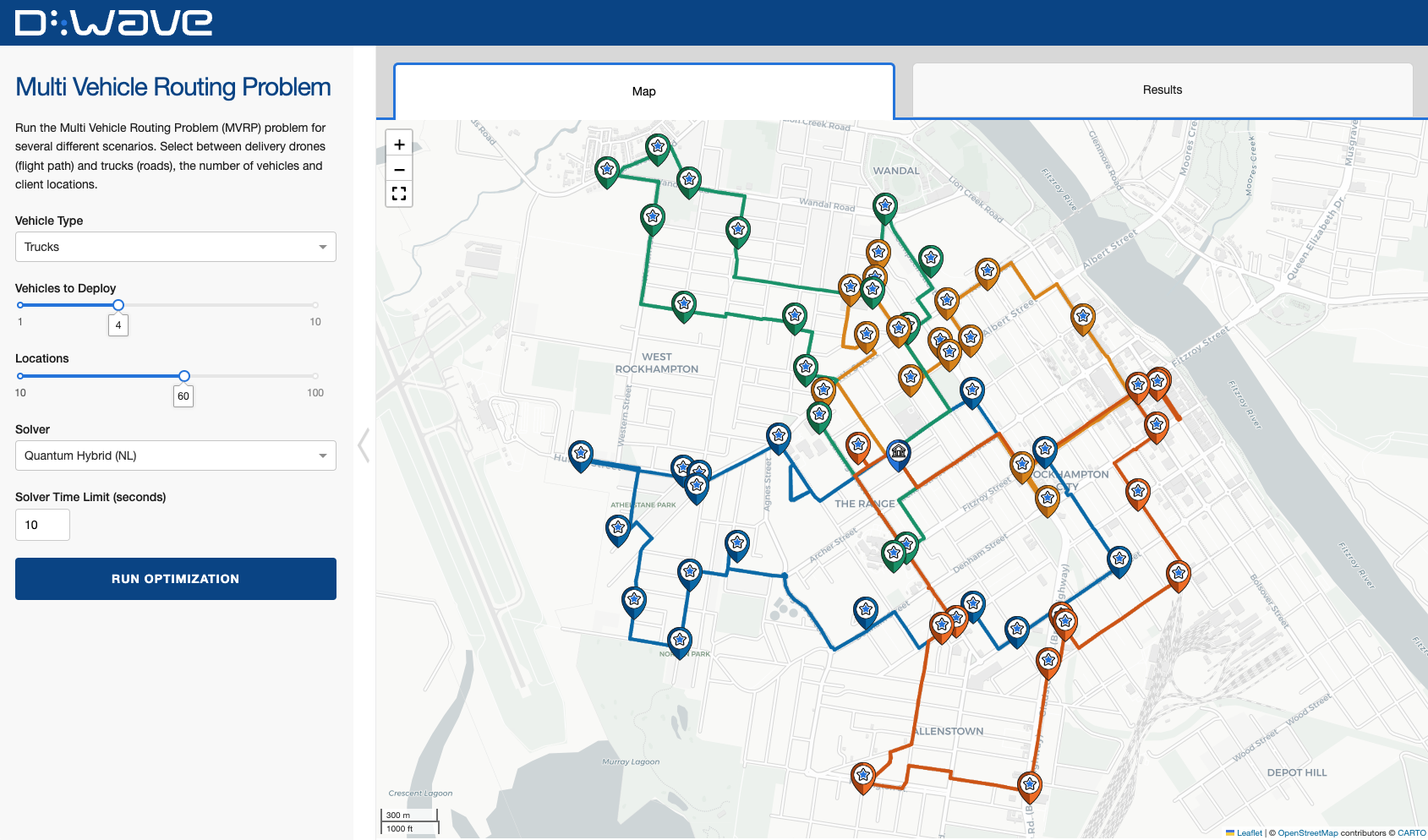
Run the Multi Vehicle Routing Problem (MVRP) problem for several different scenarios. Select between delivery drones (flight path) and trucks (roads), the number of vehicles and client locations.
You can run this example without installation in cloud-based IDEs that support the Development Containers specification (aka "devcontainers").
For development environments that do not support devcontainers, install requirements:
pip install -r requirements.txtIf you are cloning the repo to your local system, working in a virtual environment is recommended.
Your development environment should be configured to access Leap’s Solvers. You can see information about supported IDEs and authorizing access to your Leap account here.
To run the demo:
python app.pyAccess the user interface with your browser at http://127.0.0.1:8050/.
The demo program opens an interface where you can configure problems and submit these problems to a solver.
Configuration options can be found in the app_configs.py file.
The multi-vehicle routing problem is to deliver a set of resources to a set of predetermined locations using a limited number of vehicles, all of which start and finish at a single depot location.
This problem can be seen as a generalized traveling salespersons problem (TSP) where each vehicle must traverse a local network of locations in the most effective way, while also optimizing the distribution of sets of locations among the vehicles.
In this demo a single central depot location is determined by choosing an address (can be set in app_configs.py), after which a number of locations are placed randomly within a specified radius of the depot. The vehicles can either be trucks, following the road network, or drones, traversing the map as the crow flies. The problem can then be solved using either a classical or a quantum hybrid solver for a chosen number of vehicles and locations.
Released under the Apache License 2.0. See LICENSE file.