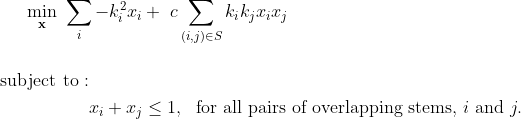RNA Folding

In biology and chemistry, the properties of a molecule are not solely determined by a set of atoms but also by the shape of the molecule. In genetics, the shape of an RNA molecule is largely determined by how it bends back on itself. The sequence of A’s, U’s, G’s, and C’s that make up RNA has certain pairs that are drawn together to form hydrogen bonds. A sequence of several bonds in a row is called a stem, and a stem provides sufficient force to keep the molecule folded together. RNA molecules naturally form some stems while avoiding others in a manner that minimizes the free energy of the system.

This demo program takes an RNA sequence and applies a quadratic model in pursuit of the optimal stem configuration.

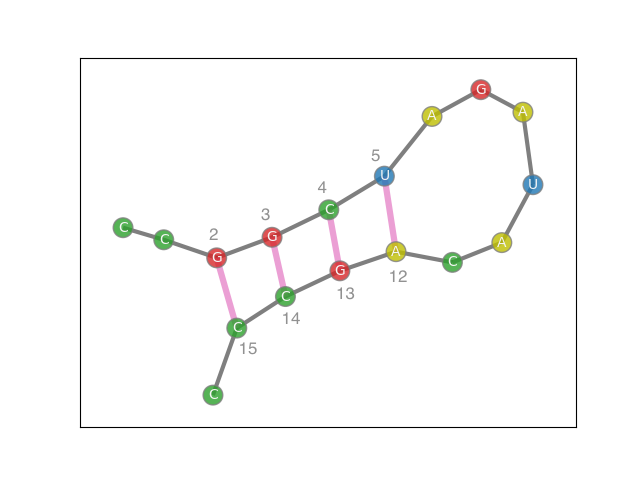
Fig.1 - An RNA sequence with a single stem of length 4.

Predicting the existence of stems is important to predicting the properties of the RNA molecule. However, prediction is complicated by two important factors.

First, stems are not allowed to overlap. A simple case of overlapping can be illustrated by Figure 1. The stem expressed by the pink lines can be denoted with the tuple (2, 5, 12, 15). Here, indexing starts with 0 at the far left C and continues along the sequence represented by the gray edges, ending with index 16 at the bottom-most C. The indices of the eight nucleotides in the stem are labeled in the figure. The four pink edges illustrate the four bonds that make up the stem. While there are eight nucleotides in the stem, bonded along pink lines, the 4-tuple completely determines the stem. However, the smaller stems (2, 4, 13, 15) and (3, 5, 12, 14) also need to be considered, even though the optimal solution will not include them in this case. Note that by default, we will only consider stems with length at least 3, as smaller stems are unlikely to form and sustain bonds.

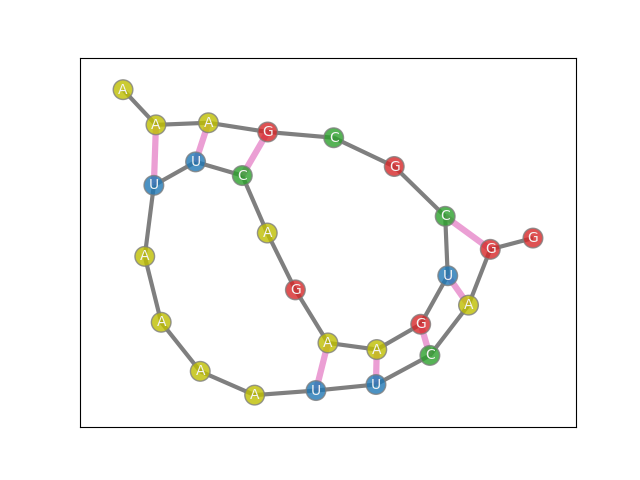
Second, the intertwining phenomenon known as a pseudoknot is less energetically favorable. In Figure 2, we see an example of such a pseudoknot, where one side of a stem occurs in between the two sides of a different stem. The use of a quadratic objective allows us to make pseudoknots less likely to occur in optimal solutions, increasing overall accuracy. Specifically, we include a quadratic term for each pair of stems that, if present, form a pseudoknot. The positive coefficient on this quadratic term discourages the forming of pseudoknots without explicitly disallowing them.

Fig.2 - A pseudoknot formed by a stem of length 3 and a stem of length 5.

This demo is loosely based on the work in [1], which is in turn inspired by [2].

Usage

To run the demo through a command line interface, type:

python RNA_folding.py

The demo prints the optimal stem configuration along with other relevant data. It then saves a plot of the sequence and its bonds as RNA_plot.png.

Optional parameters

Several optional parameters are accepted:

--path: specifies the path to an input text file with RNA sequence information.
--verbose: prints additional information about the model when set to 'True' (the default).
--min-stem: minimum length necessary for a stem to be considered.
--min-loop: minimum number of nucleotides that must be present in between the two sides of a stem for that stem to be considered. In the literature, this is termed a 'hairpin loop.'
-c: reduces the likelihood of pseudoknots by setting larger values of the coefficient, ck_ik_j, applied to the quadratic pseudoknot terms.

As an example, to explicitly call the default values, type:

python RNA_folding.py --path RNA_text_files/TMGMV_UPD-PK1.txt --verbose True  --min-stem 3 --min-loop 2 -c 0.3

Problem Formulation

In predicting the stems of an RNA molecule, we build a quadratic model with three contributing factors.

Each potential stem is encoded as a binary variable, linearly weighted by the negative square of the length, k.
Each potential pseudoknot is encoded as a quadratic term, weighted by to the product of the two lengths times a positive parameter c.
Overlapping stems are not allowed. Potential overlaps give rise to constraints in the model.

Here, each x_i is a binary variable indicating the inclusion/exclusion of the i^th stem. Each constant k_i is the length of said stem. The indexing set S is the set of all pairs of stems that form a pseudoknot. Finally, c is a tunable parameter adjusting the impact of pseudoknots. It is set to 0.3 by default. If c = 0, the affect of pseudoknots is ignored, while c > 1 eliminates all pseudoknots from optimal solutions. This formulation (and default choice of c) is loosely based on [1].

In the printed solution, each stem is denoted by four numbers. The first two numbers correspond to the beginning and ending indices of the first side of the stem. Similarly, the last two numbers correspond to the beginning and ending indices of the second side of the stem.

Code Overview

The implementation can be broken into three main parts

Preprocessing the RNA sequence to extract all possible stems, pseudoknots, and overlaps.
Building the model and sending it to a hybrid solver to find a solution.
Post-processing the solution to print appropriate information and create the plot.

A majority of the code is dedicated to step 1. Here, possible bonds are stored in a binary matrix, and the matrix is searched for possible stems. Possible stems (each corresponding to a decision variable) are stored in a dictionary structure that reduces the number of comparisons necessary when searching for pseudoknots and overlaps.

Code Specifics

By default, the minimum stem length is set to 3. A stem of length 5 thus contains two stems of length 4 and three stems of length 3 under inclusion. The stem dictionary records the maximal stems (under inclusion) as keys, where each key maps to a list of the associated stems weakly contained within the maximal stem.

No two stems contained in the same maximal key can both be in an optimal solution, so we treat them all as overlapping, regardless of if it is literally the case. This particular case of overlapping is enforced by treating the set of stems contained in a maximal stem as a single discrete variable by use of the add_discrete method.

We further use the stem dictionary structure to avoid comparing all combinations of stems when searching for pseudoknots and overlaps.

Plotting uses a randomized process to find a reasonable layout. For this reason, the plot will change in successive runs, even if the solution does not.

Input text files should have a number at the beginning of each line, followed by a sequence of A, C, G, U, and T's. The file reader ignores the leading number and is not sensitive to spaces, upper vs. lower case, or line breaks. By convention, spaces are used to separate every 10 letters and the number at the beginning of each line is included to keep track of the location in the sequence. For instance, if there are 30 letters on each line, then there would be three groups of 10 letters on each line, with the leading numbers increasing by 30 each line.

References

[1] Fox DM, MacDermaid CM, Schreij AM, Zwierzyna M, Walker RC. "RNA folding using quantum computers," PLOS Computational Biology.

[2] Kai, Zhang, et al. "An efficient simulated annealing algorithm for the RNA secondary structure prediction with Pseudoknots," BMC Genomics.