Don Williamson (@donzanoid) 4 August, 2002
Well, I'm in southern France having a whale of a time on a camp-site in beautiful weather, so what a perfect time this would be to look at arc-length parameterisation! This zip contains a little bit of the research I did while on holiday, geared towards various techniques in animation. Hopefully it should make this information more accessible to those who find themselves involved with all this stuff for whatever reason.
To compile this source fully you're going to need SDL (a brilliant piece of work) and my SDLApp framework, which should be available on my website. Go to www.libsdl.org for all SDL-related info.
The simple goal of this exercise is to be able to accurately control the speed at which parameters interpolate over any given type of curve.
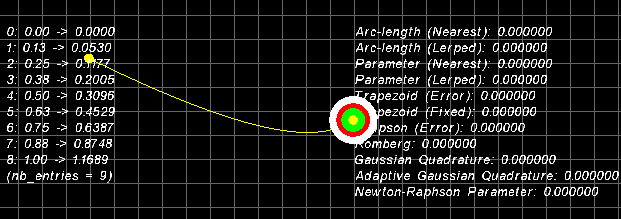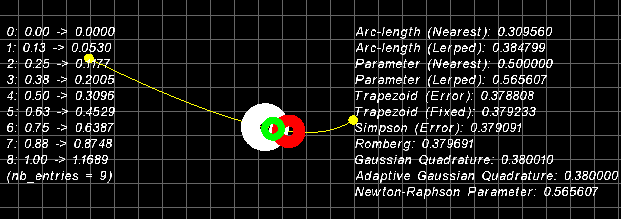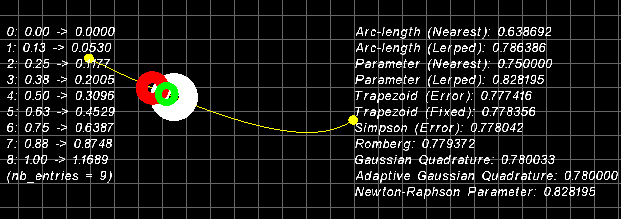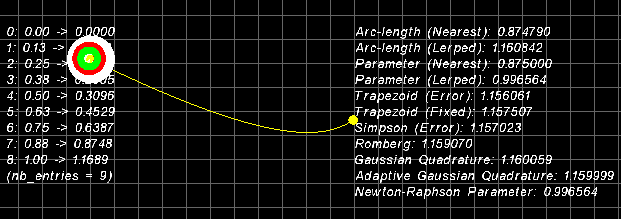
The columns down the left of the screen display the arc-length/parameter pairs in
the adaptive or fixed tables. The values on the right are the various arc-lengths and
parameters generated by the numerous techniques implemented in this code. The yellow line
with two circles at each end is a randomnly generated cubic curve. You can generate others
by pressing the [SPACE] bar. The white ring is moving at a constant speed along the curve,
you can see this speed at the bottom right hand side of the screen. The red ring is
moving via a simple sine ease function and the green ring is moving via another ease
function which provides constant velocity within parametric bounds.
The different parameterisation methods are discussed below.
Step along the curve at fixed intervals sampling the points. For each point you sample store it's parametric value along with distance from the beginning of the curve in a table.
Mapping from parameter value to arc-length involves simply dividing the parameter value by the interval size and using that as an index into the table, finding the nearest arc-length. Less coarse arc-lengths are also provided by linearly interpolating between the two closest table entries.
Mapping from arc-length to parameter value is done through a binary search on the arc-length values which is reasonably fast for picking random points on the curve. Even better results can be obtained by using a correlated search algorithm on the arc-lengths such as the hunt function in Numerical Recipes, but only if you're following the path rather than picking random points on it.
A fixed-size table will undersample areas of high non-linearity and invest wasted time in oversampling highly linear areas. Use recursive subdivision to generate a table that plots more samples in areas of high non-linearity.
Mapping from parameter value to arc-length is not so simple this time because the sample points aren't evenly spaced. A binary search, or hunt, can be used in this scenario, again linearly interpolating between successive entries when the nearest has been found.
Mapping from arc-length to parameter value is exactly the same as doing it for a fixed size table.
The arc-length integral:
integral[modulus[dP/du], u0, u1]
cannot be analytically solved so you can use a selection of algorithms to approximate the integral. Mapping from parameter value to arc-length can be done in a number of ways, including the following (all in the source):
Very basic sampling of the function to be integrated at evenly spaced intervals with non-varying weights. Can be done using a fixed interval size or adaptive sample size through recursive refinement of the approximation.
A simple extension of the trapezoidal rule where the approximation is calculated in pairs of sucsessive trapezoidal refinements, and weighted so as to cancel out the leading error term introduced by the first pass.
Simpsons rule is a special case of romberg integration, which is used for integration schemes that are of a higher order than Simpson's rule. Polynomial extrapolation is used to cancel out leading error terms, of which, the pair approach in Simpson's rule is again a special case.
For every point set containing N points there exists a unique polynomial of order N-1 that interpolates through those points (e.g. for 2 points there exists a unique line that interpolates through them). This simple brute force algorithm will evaluate that polynomial at any given point, given the point list.
An improvement on lagrange which recursively works up from polynomials of zero'th order to the desired order. Much faster than lagrange, and provides an error estimate as a result of the interpolation/extrapolation.
Uses unevenly spaced intervals in an attempt to get the greatest accuracy using the smallest number of function evaluations. Hence this is a very efficient algorithm and the numerical integration algorithm of choice. This algorithm can allow as much as twice much order as that in previous algorithms which can mean much higher accuracy if the function can be well-approximated by a polynomial.
Mapping from arc-length to parameter value can be done with newton-raphson iteration, where:
Pn+1 = Pn - f(Pn)/f'(Pn)
f(Pn) = Arc-length integral at Pn
f'(Pn) = dP/du evaluated at Pn
The iteration converges very quickly on the root and requires little calculation at each iteration.
Gaussian quadrature, just like fixed-size table lookups, is capable of oversampling and undersampling. This can be solved by using an adaptive gaussian method. Build an adaptive-size lookup table as in method (2) but use gaussian quadrature to approximate the arc-lengths instead of simple linear distance.
Mapping from parameter value to arc-length is first of all done by locating the nearest parameter value below your search value using a binary search as in method (2). Then instead of linearly interpolating the located arc-length, use gaussian quadrature to calculate the arc-length from the located parameter to your requested parameter; the parameter range having been reduced enough to make this gaussian quadrature approximation very accurate.
Mapping from arc-length to parameter value can be done as with the numerical integration techniques since the arc-length integral needs to be evaluated at each iteration, making it an already adaptive evaluation.
The most accurate combination I've found is adaptive gaussian quadrature for mapping parameter to arc-length, combined with newton-raphson iteration for mapping arc-length to parameter. The newton-raphson stage can be accelerated greatly by doing a binary (or correlated) search through the table built by the AGQ routine and linearly interpolating between closest parameter values to generate the initial guess for the iteration. The remaining steps only require a few iterations of Newton-Raphson to get very close to the real root in a very efficient manner.
The current implementation (compiled EXE) contains the above methods as default and you can see by looking at the speed parameter how accurate the methods really are. As a comparison, if you replace all calls to GetParameterNewtonRaphson() with calls to GetParameterAdaptiveLerped(), you'll notice a large change in the variability of the speed parameter.
Additionally, the added accuracy of gaussian quadrature and newton-raphson allow the table sizes to be a lot smaller than the linear-distance based methods.
- Rick Parent, "Computer Animation, Algorithms and Techniques"
- William H. Press et al, "Numerical Recipes in C"