The task requires efficient processing of a large number of rectangles and points. Three different algorithms were implemented and tested to determine the most efficient one. The algorithms were tested on different volumes of initial data and points to determine their efficiency. The results of the tests were analyzed to determine the most efficient algorithm for this task.
The laboratory work consists of implementing and comparing the performance of three different algorithms:
- Brute Force Algorithm
- Compressed Map Algorithm
- Persistent Tree Algorithm
Each algorithm was implemented in Rust and tested on a dataset of [1..200000] points and [1..200000] rectangles.
To run tests, follow these steps:
- Clone the repository
- Read Installation from 'The Rust Programming Language' book.
- Navigate to the project directory in your terminal
- Run
cargo build --releaseto build the project - Run
cargo test -r -- --show-outputto run the project
The measured complexity that was given before:
| Algorithm | Time Complexity | Preparation |
|---|---|---|
| Brute Force | O(N) | O(1) |
| Compressed Map | O(log(N)) | O(N^3) |
| Persistent Tree | O(log(N)) | O(Nlog(N)) |
The below graphics provide an explanation of the complexity and comparison of the algorithms:
| Algorithm on map | Algorithm on persistent tree |
|---|---|
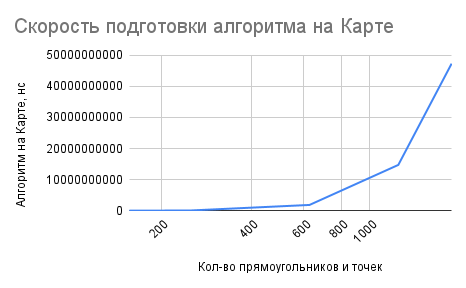 |
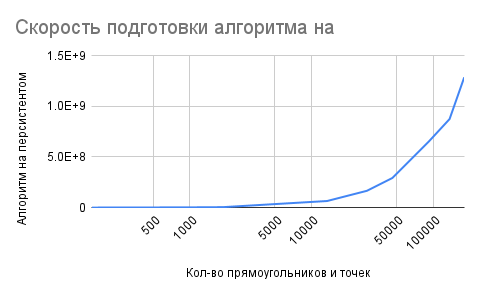 |
| Comparison of algorithm on the persistence tree and on the map |
|---|
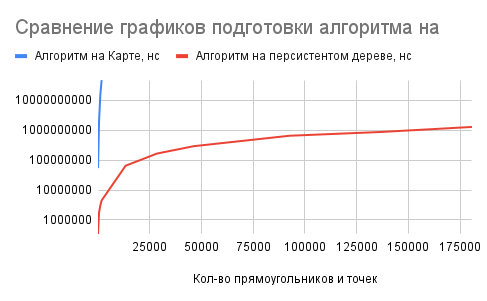 |
| Average time complexity of algorithms |
|---|
.png) |
The results showed that the map algorithm was the slowest in the preparation phase, taking O(n^3) to build the 2D map on compressed coordinates. On the other hand, the brute force algorithm had a complexity of O(1) in preparation (because doesn't have it :) ), while the persistent tree algorithm prepared itself in O(n log(n)). The persistent tree and the algorithm on the map did not overlap in terms of data preparation complexity, which tells us that the algorithm on the map takes much longer to prepare the data.
The graph indicates that the brute force algorithm has a consistent time complexity of O(n) for data queries, whereas the other two algorithms have time complexities of around O(log(n)). Based on this, we can infer that all three algorithms perform equally well in responding to requests until the number of rectangles reaches approximately 500.
In my analysis, I found that the brute force algorithm may be the most efficient for smaller datasets, while the persistent tree and algorithm on map may be more efficient for larger datasets.