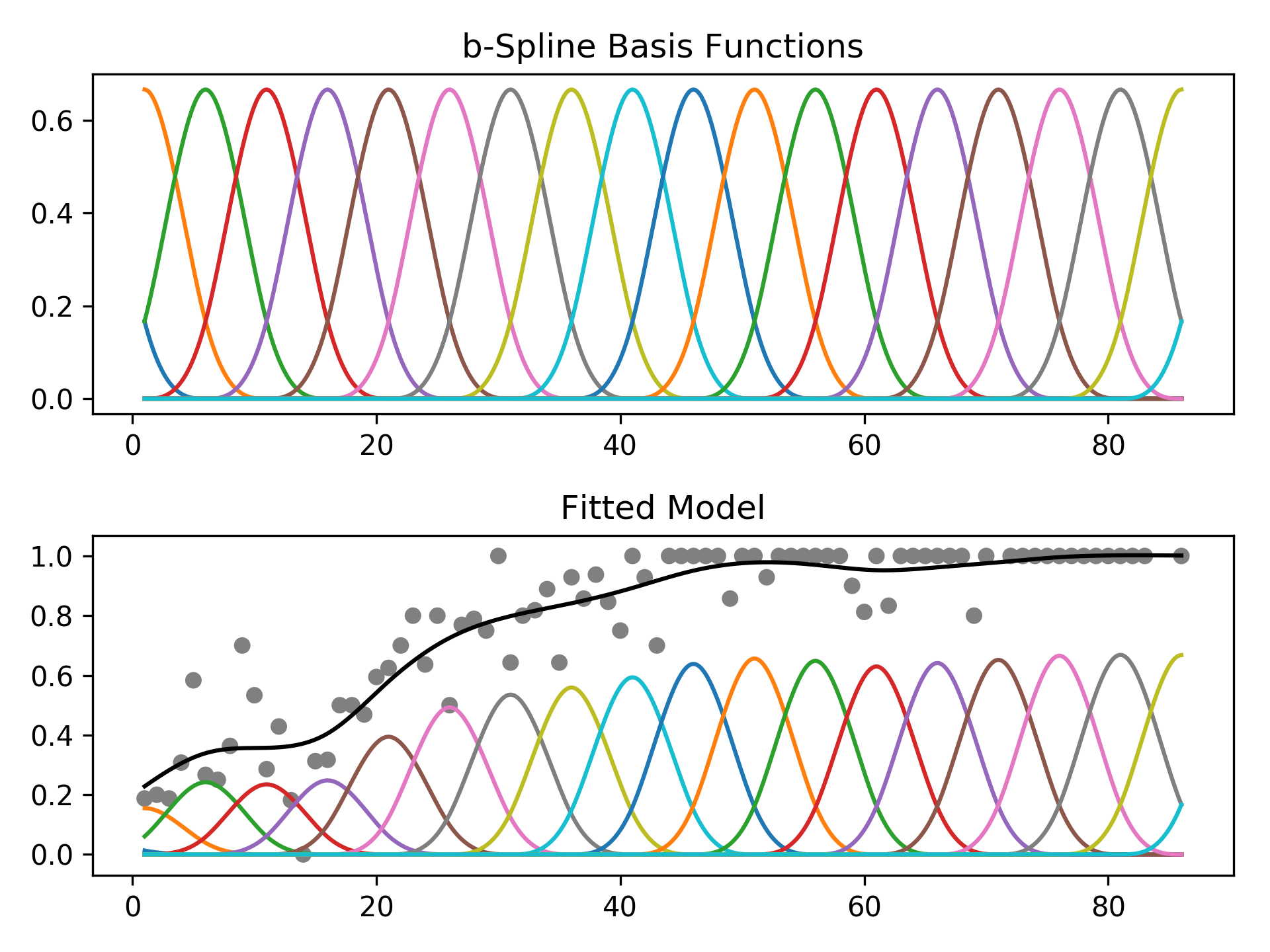
Generalized Additive Models in Python.
- Official pyGAM Documentation: Read the Docs
- Building interpretable models with Generalized additive models in Python
pip install pygam
To speed up optimization on large models with constraints, it helps to have scikit-sparse installed because it contains a slightly faster, sparse version of Cholesky factorization. The import from scikit-sparse references nose, so you'll need that too.
The easiest way is to use Conda:
conda install -c conda-forge scikit-sparse nose
Contributions are most welcome!
You can help pyGAM in many ways including:
- Working on a known bug.
- Trying it out and reporting bugs or what was difficult.
- Helping improve the documentation.
- Writing new distributions, and link functions.
- If you need some ideas, please take a look at the issues.
To start:
- fork the project and cut a new branch
- Now install the testing dependencies
conda install pytest numpy pandas scipy pytest-cov cython
pip install --upgrade pip
pip install -r requirements.txt
It helps to add a sym-link of the forked project to your python path. To do this, you should install flit:
pip install flit- Then from main project folder (ie
.../pyGAM) do:flit install -s
Make some changes and write a test...
- Test your contribution (eg from the
.../pyGAM):py.test -s - When you are happy with your changes, make a pull request into the
masterbranch of the main project.
Generalized Additive Models (GAMs) are smooth semi-parametric models of the form:
where X.T = [X_1, X_2, ..., X_p] are independent variables, y is the dependent variable, and g() is the link function that relates our predictor variables to the expected value of the dependent variable.
The feature functions f_i() are built using penalized B splines, which allow us to automatically model non-linear relationships without having to manually try out many different transformations on each variable.
GAMs extend generalized linear models by allowing non-linear functions of features while maintaining additivity. Since the model is additive, it is easy to examine the effect of each X_i on Y individually while holding all other predictors constant.
The result is a very flexible model, where it is easy to incorporate prior knowledge and control overfitting.
Please consider citing pyGAM if it has helped you in your research or work:
Daniel Servén, & Charlie Brummitt. (2018, March 27). pyGAM: Generalized Additive Models in Python. Zenodo. DOI: 10.5281/zenodo.1208723
BibTex:
@misc{daniel\_serven\_2018_1208723,
author = {Daniel Servén and
Charlie Brummitt},
title = {pyGAM: Generalized Additive Models in Python},
month = mar,
year = 2018,
doi = {10.5281/zenodo.1208723},
url = {https://doi.org/10.5281/zenodo.1208723}
}
-
Simon N. Wood, 2006
Generalized Additive Models: an introduction with R -
Hastie, Tibshirani, Friedman
The Elements of Statistical Learning
http://statweb.stanford.edu/~tibs/ElemStatLearn/printings/ESLII_print10.pdf -
James, Witten, Hastie and Tibshirani
An Introduction to Statistical Learning
http://www-bcf.usc.edu/~gareth/ISL/ISLR%20Sixth%20Printing.pdf -
Paul Eilers & Brian Marx, 1996 Flexible Smoothing with B-splines and Penalties http://www.stat.washington.edu/courses/stat527/s13/readings/EilersMarx_StatSci_1996.pdf
-
Kim Larsen, 2015
GAM: The Predictive Modeling Silver Bullet
http://multithreaded.stitchfix.com/assets/files/gam.pdf -
Deva Ramanan, 2008
UCI Machine Learning: Notes on IRLS
http://www.ics.uci.edu/~dramanan/teaching/ics273a_winter08/homework/irls_notes.pdf -
Paul Eilers & Brian Marx, 2015
International Biometric Society: A Crash Course on P-splines
http://www.ibschannel2015.nl/project/userfiles/Crash_course_handout.pdf -
Keiding, Niels, 1991
Age-specific incidence and prevalence: a statistical perspective