This repository collects relevant methods in the field of military operations research. It aims to approach the topics from the application side, while reducing the theoretical background to the bare minimum.
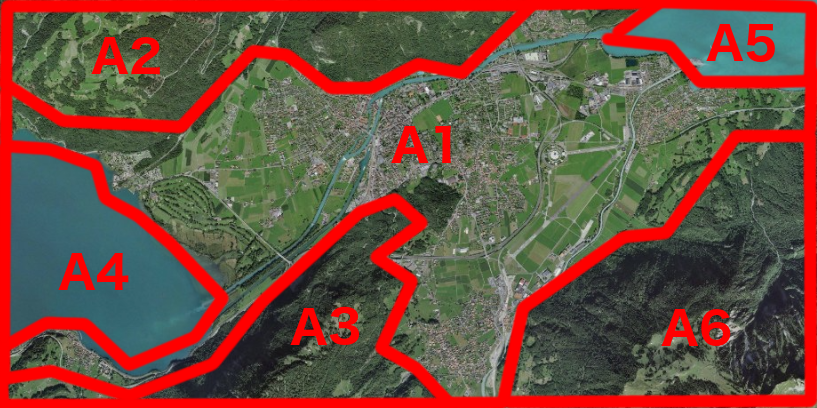
This method is about optimizing search efforts in order to maximize the probabilty of detecting a potential opponent. Considering the depicted situation below, it is self-evident that the propability of presence of enemy troops is nonuniform among the given areas A1 to A6. If the opposing force has a strong marine and mechanized infantery, there is less chance of finding anything on a steep mountain side than on urban territory.
The presented method is a numerical recipe for finding the best possible search strategy. In particular, it will determine, respectively optimizing, the search efforts in each area A1 to A6 in order to reach the highest accumulated probability of a search success. The applied mathematical model is derived from the random search formula of Koopman and results in following optimization task:
Please note that are the parameters to optimize and represent the search effort in time invested in the corresponding region, whereas
denotes the overall available search time.
The sensor parameters
is the sweep width and
the scanning speed.
is a regions areal size and
the probability that a target might be located there.
is the overall probability of detection and core objective.
Let's stick to above situation with the potential presence of tanks and battle ships.
The sweep width is and
.
The table below summarizes the properties of the regions.
| Type | |||
|---|---|---|---|
| Area 1 | urban | 14.1 | 0.55 |
| Area 2 | mountain | 6.3 | 0.05 |
| Area 3 | mountain | 4.1 | 0.05 |
| Area 4 | water | 3.5 | 0.15 |
| Area 5 | water | 1.9 | 0.15 |
| Area 6 | mountain | 9.1 | 0.05 |
Here is a little example of how such a problem can be solved by using scipy's SLSQP solver with constraints.
Note that there might exist better approaches to tackle this task.
The following table summarizes the optimal search strategies for different total search efforts of hours.
| 3 hours effort | 5 hours effort | 8 hours effort | 13 hours effort | |
|---|---|---|---|---|
| Area 1 | 2.00 h | 3.22 h | 4.45 h | 6.27 h |
| Area 2 | 0.00 h | 0.04 h | 0.57 h | 1.40 h |
| Area 3 | 0.00 h | 0.27 h | 0.64 h | 1.16 h |
| Area 4 | 0.54 h | 0.84 h | 1.15 h | 1.60 h |
| Area 5 | 0.45 h | 0.62 h | 0.79 h | 1.03 h |
| Area 6 | 0.00 h | 0.00 h | 0.40 h | 1.56 h |
| Optimized Detection Probability | 57.6 % | 72.4 % | 84.3 % | 93.8 % |
| Non-optimized Detection Probability | 42.5 % | 60.3 % | 77.2 % | 90.9 % |
Reference: Military Operations Research, Jaiswal
Many reconnaissance tasks in military are about localizing enemy threats.
Not seldom these information are redundant and a good approach is to consider them all.
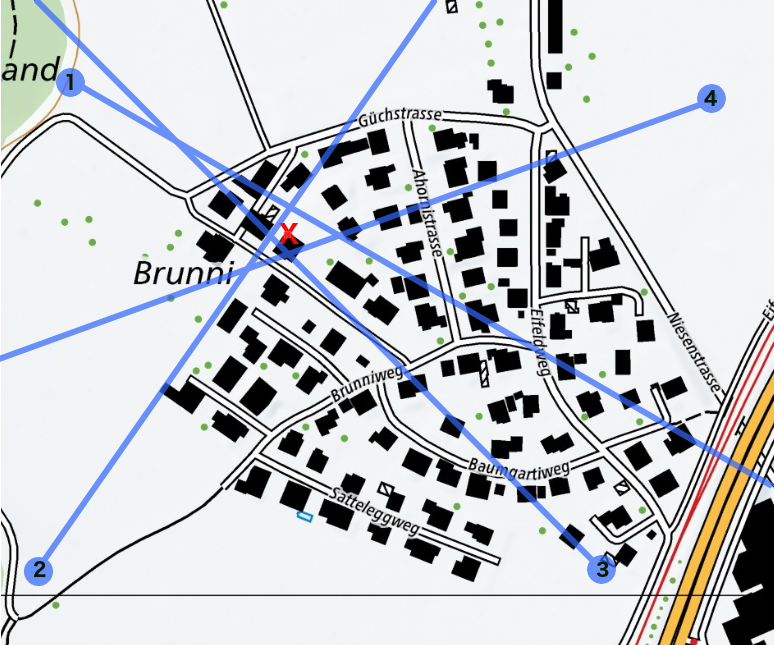
In the following example it is shown how the optimal target position is computed based on multiple sensors
on different location.
Solely the individula direction
towards the spotted target and the sensor's position
is of interest.
The optimal target position minimizes the accumulated distances to each sensor line, where the distance refers to the minimal distance
between a point and a line.
| 1 | -30 | (2615050.2, 1170313.8) |
| 2 | 55 | (2615030.5, 1170021.7) |
| 3 | 135 | (2615367.0, 1170022.6) |
| 4 | 200 | (2615434.7, 1170302.6) |
The optimal target location is marked by a red X.
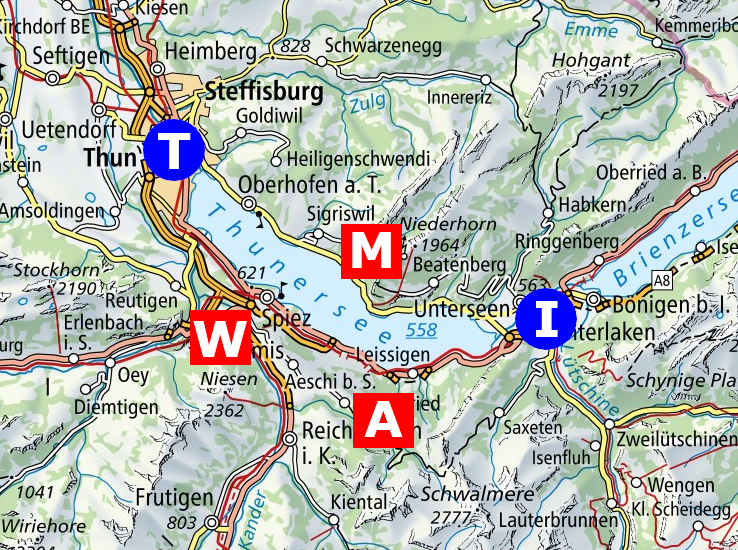
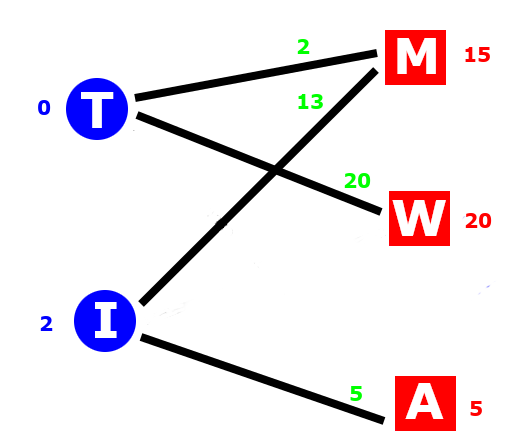
Logistics is an important aspect in military operations. Transporting the required equipment in an effective manner from one place to the other is, therefore, crucial. Following example depicts a simple transportation problem, in which one certain type of missile system is shipped from two depots (blue) to three destinations (red). The optimal transportation strategy is the one requiring the least accumulated driving distance.
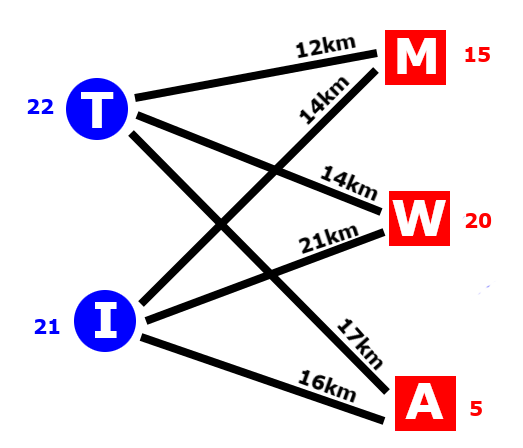
The figure below is a more regular way of representing such a transportation task. The blue number next to the depot indicates the number of missile systems which are available at this base. The red number right of the destination is the number of systems required at this side. The black number above the edge is the corresponding distance from the depot to the destination.
This problem can be solved by Linear Programming.
Let us assume the optimal transportation of the form , where for example the first element
holds the number of missile systems moved from deopt T to destination M, and so on.
The linear program of this particular problem looks as follows:
The obective function (accumulated distance) to be minimized
Two constraints on the depot sides
The constraints on the destination sides
Further on there is nothing like negative transportations, so
Solving this linear program leads to following optimal transportation process. The green numbers denote the delivered missile systems from a depot to a destination. The corresponding accumulated transportation distance is 566 km.
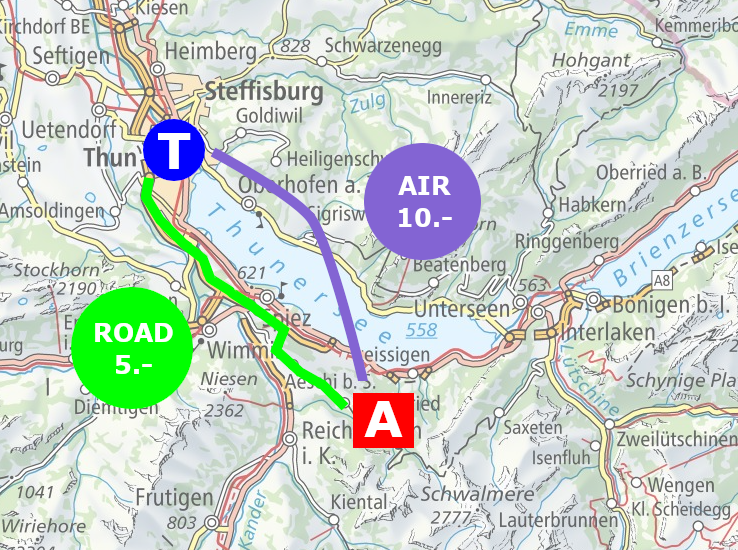
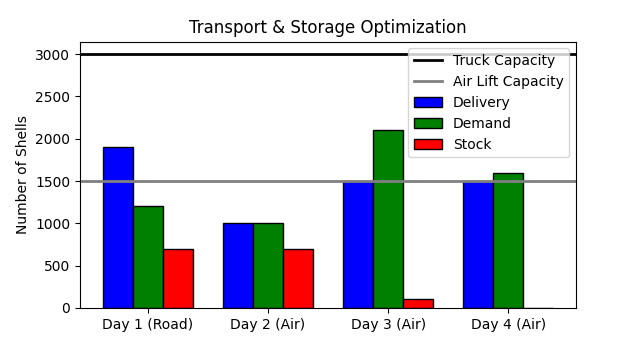
This example is a more advanced version of the previous logistics problem. Instead of a single factor, here we deal with multiple aspects. It is assumed that during the next four days there will be heavy air attacks. Location A is a favourable position to ramp up a mobile air defence station. Our responsibility is the planning of a costeffective shipment of ammunition, shells, from depot T to location A, by considering following given constraints:
- At day 1, the shells can be transported on the road by truck. Maximum 3000 pieces for 5 CHF per piece.
- It is assumed that the air attacks at day 1 destroy the roads. Thus, the transportation at day 2, day 3 and day 4 are excecuted with an helicopter. Maximum 1500 pieces at a transportation price of 10 CHF per piece.
- Digging the shells' storage place and guarding the ammunition is very labour intensive, and therefore cost relevant. Storing 1 shell for 1 day costs 3 CHF. Increasing or decreasing the storage place costs 5 CHF per shell.
This optimization problem can be solved with Linear Programming. Here is the actual code which executes the optimization. There are some nice tricks which are pointed out in the source. The figure below shows the optimal logistics.
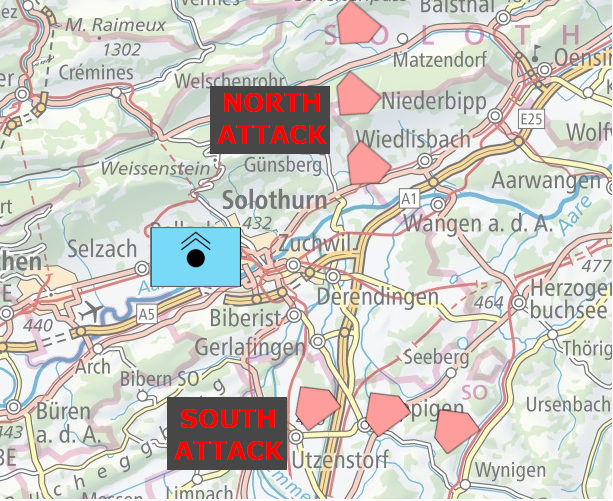
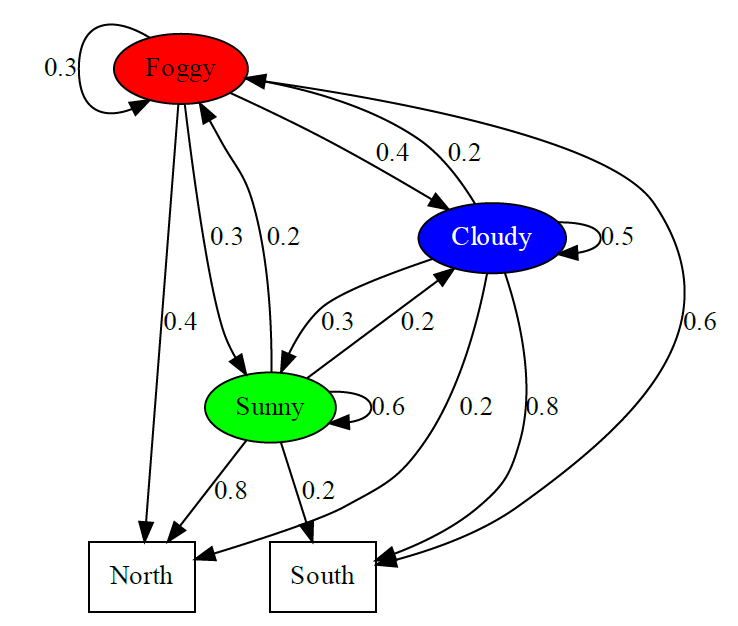
A command headquarter in a little city is repeatedly attacked by hostile planes over several weeks. A retired mathematician living nearby is annoyed because of the unbearable noise and decides to take care of it. Soon she finds out that the attacks are coming either from the South or over the mountain chain in the North.
Further on, there seems to be a pattern in the north / south attack sequence. If yesterday's assault came from the north, today's comes likely also from the north. The same applies to south attacks. She decides to visit the command headquarter and tell the soldiers about her findings. To her surprise a whole team is already working on this very same problem. There is a strong correlation between the weather at the enemy's airport and the side from which the city is attacked. Due to limited resources the headquarter does not know the exact weather at the enemy's airport and can establish these links only retrospectively. The responsible soldiers have a lot of detailed knowledge but are overwhelmed with the task of combining all these aspects. Not so the mathematician. With the input of the soldiers and reviewing long term weather statistics she comes up quickly with a Hidden Markov Model and following code. The transition probabilities of foggy, rainy and sunny periods together with observations of previous attacks, allows an estimation for tomorrow's battle.
Given the attack sequence of the last 12 days - NORTH, NORTH, SOUTH, SOUTH, NORTH, NORTH, SOUTH, NORTH, SOUTH, SOUTH, SOUTH, NORTH - there is a higher chance that tomorrow's attack comes from the North.