MRPT (Multiple Random Projection Trees) is an algorithm for approximate nearest neighbor search in high dimensions. The method is based on combining multiple sparse random projection trees using a novel voting scheme where the final search is focused to points occurring in candidate sets retrieved by multiple trees. MRPT is a result of research conducted at the Helsinki Institute for Information Technology (HIIT).
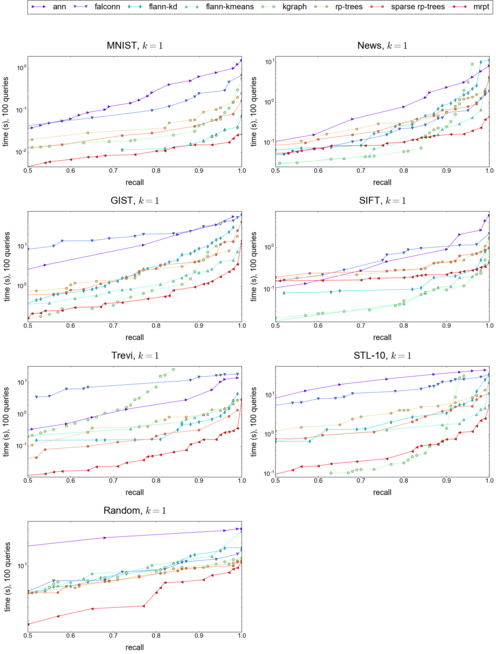
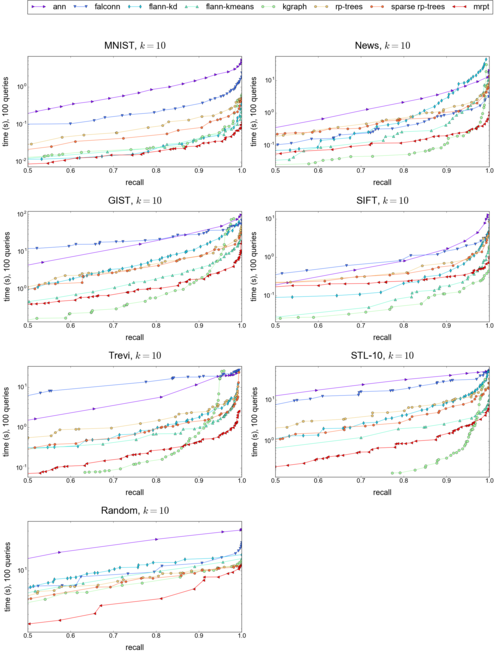
This project contains a performance comparison between MRPT and other state-of-the-art libraries for approximate nearest neighbor search. We focus on high-dimensional real-world data sets. The performance of the algorithms is measured in terms of query time and recall, that is, the fraction of true nearest neighbors returned. All of the experiments were performed on a system with two Intel Xeon E5540 2.53GHz CPUs and 32GB of RAM. No parallelization was used in any of the experiments.
The MRPT algorithm is described in detail in the paper
Hyvönen, V., Pitkänen, T., Tasoulis, S., Jääsaari, E., Tuomainen, R., Wang, L., Corander, J. & Roos, T. (2016, December). Fast nearest neighbor search through sparse random projections and voting. In Big Data (Big Data), 2016 IEEE International Conference on (pp. 881-888). IEEE
Note that this repository only contains the version of MRPT used for the experiments in the above paper. An updated version with Python bindings and Windows support is available here.
The included libraries are:
The included data sets are:
| data set | n | d | type of data |
|---|---|---|---|
| MNIST | 60000 | 784 | images of hand-written digits |
| News | 262144 | 1000 | web pages converted into TF-IDF representation |
| GIST | 1000000 | 960 | global color GIST descriptors |
| SIFT | 2500000 | 128 | local SIFT descriptors |
| Trevi | 101120 | 4096 | image patches |
| STL-10 | 100000 | 9216 | images of different classes of objects |
| Random | 50000 | 4096 | random samples from the 4096-dimensional unit sphere |
For each data set, we use a disjoint random sample of 100 points as the test queries.
For the most important tuning parameters (as stated by the authors), we use grid search on the appropriate ranges to find the optimal parameter combinations in the experiment, or the default values whenever provided by the authors. The exact parameters for each data set can be found in the parameters folder. Note that while in some cases the performance could possibly be improved by increasing the memory consumption or index building time, the parameters are chosen such that these were feasible on the test system. This applies to our method as well.
The performance of MRPT is controlled by the number of trees, the depth of the trees and the vote threshold. For ANN, we vary the error bound, and for FLANN, we control the accuracy primarily by tuning the maximum number of leafs to search, but also vary the number of trees for k-d trees and the branching factor for hierarchical k-means trees. KGraph is primarily controlled by the search cost parameter, but we also build the graph with varying number of nearest neighbors for each node. For FALCONN, we search for the optimal number of hash tables and hash functions.
Results for k = 1, 10 and 100 (click on the images to enlarge):
| k = 1 | k = 10 | k = 100 |
|---|---|---|
 |
 |
 |
In addition, we include interactive plots to explore the optimal parameters and tables that summarize the results.
The algorithms and data sets can be downloaded by running:
./get_algos.sh
./get_data.sh
The comparisons can then be run individually for the data sets, for example:
./comparison.sh mnist
elias.jaasaari at gmail.com