- Unveils internal "invisible" patterns automatically
- https://github.com/enfeizhan/clusteror
- Fei Zhan
- License: MIT License
This package is developed in Python 3.4. However support for Python 2 will be in the next release.
This is a tool for discovering patterns existing in a dataset. It can be useful in segmenting customers based on their demographic, geographic, and past behaviours in a commercial marketing environment. Users are encouraged to adventure with it in other scenarios.
Under the hood, a pretraining of (Stacked) Denoising Autoencoder is implemented in Python deep learning library Theano. Therefore, an installation of Theano is mandate. About how to install Theano, please read Theano installation guide.
If you are lucky to have Nvidia graphic card, with proper setup Theano can parallel the calculation to be able to scale up to large datasets.
The purpose of Unsupervised Machine Learning is to find underlying patterns without being provided with known categories as Supervised Classification Machine Learning. While it sounds like the most leveraged use case of Machine Learning as it does not rely on expensive labels that generally need to be created by human, its efficiency is debatable for commonly seen algorithms.
Recall the very first clustering algorithm in machine learning lectures, K-Means. It looks amazing for beginners. The randomly initiated centroids seem to be intelligent to know where they should gravitate to. At least for the example datasets for illustrating purposes.
But real life problems aren't that straightforward. It's not unlikely you are given a dataset that looks like this in a 2D space:
Unfortunately this is the best K-Means can do and you probably scratch you head wondering what you can do to solve this seemingly straightforward problem.
The cost function of K-Means instructs centroids to search for points located in a spharical region centring around them. This assumption of what a cluster is no doubt fails when a cluster of points resides in a stripe shape like in the example above.
This "unexpected" (actually this is a well-known fact) failure stems from that K-Means fumbles in higher dimensional space. While this terminates K-Means to be an awesome clustering tool that is deployable in extensive environments, its performance in one dimensional space has been ignored largely due to examples in two dimension are more illustrative.
Having this in mind, we would work on to search ways of reducing high dimensional dataset to one dimension. As this is truly the cause responsible for all strugglings in clustering high dimensional data.
Fortunately, the progress in Deep Learning sheds new light on this issue. As labeled dataset is expensive, experts in this area came up with the salient idea of Pre-training, which enormously reduced the amount of labeled dataset needed to train a deep learning neural network.
In a nutshell, pre-training updates the parameters in neural network such that an input can traverse the network forward and back therefore reproduce itself. A cost function is defined regarding the difference between the input and reproduced input instead of input and output.
While it's highly recommended to read research articles to gain more detail, a characteristic property of this process is tremendously useful for reducing dataset in high dimension down to lower dimension.
The central idea is given the input can be loyally or nearly loyally reproduced the neural network can be expected to do two things:
- one-to-one mapping input to output; A different input results in a different output.
- Similar inputs lead to close outputs.
These two characteristics ensure clustering done in low-dimensional space is equivalent to do the clustering in high dimension.
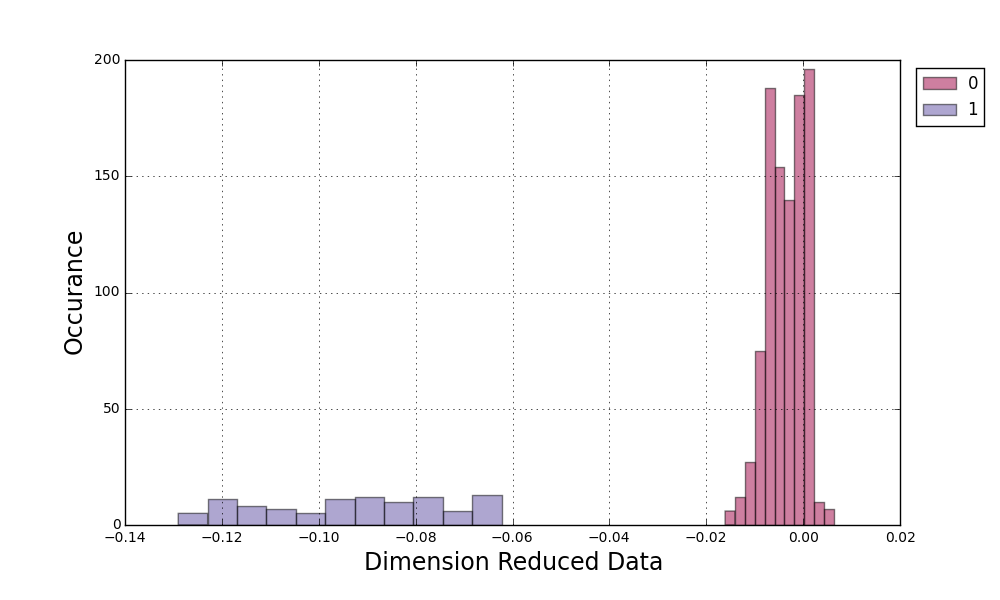
A picture is worth a thousand words. The chart below is the result of a three layer neural network:
The magic lies in how it looks in the mapped one dimensional space:
Without too much explanation, the left blue bars are the from the right blue points and the right red bars from the left red points. As there isn't concept for a sphere in 1d, K-Means works perfectly.
At the moment, you can do the following with the tools provided by the package:
- Dimension reduction to 1d.
- Clustering in 1d and assign cluster ids back to the original dataset.
- Certain useful plotting tools to display the efficiency of the clustering.
This project is still in alpha stage. In the imminent release, you can expect
- Tools to searching for the drivers that distinct the clusters.
- More support in Python versions.
This project has been set up using PyScaffold 2.5.7. For details and usage information on PyScaffold see http://pyscaffold.readthedocs.org/.