Thermosphere neural implicit representation
Report bug
·
Request feature
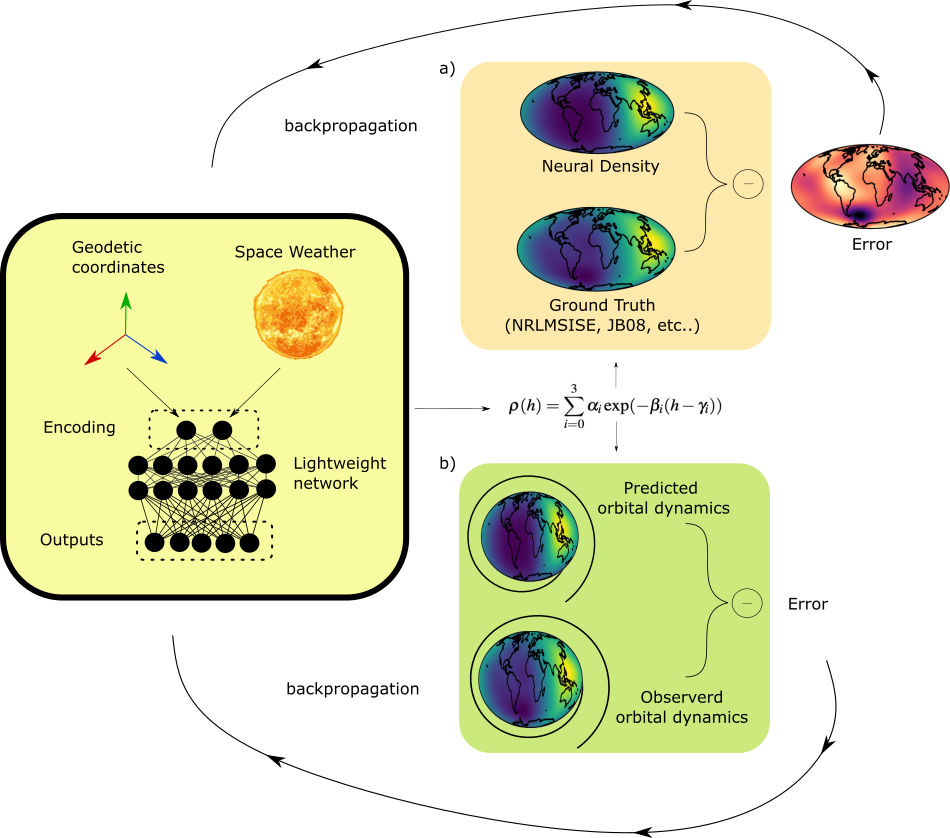
This repository introduces a novel neural architecture termed thermoNET, designed to represent thermospheric density in satellite orbital propagation, using a reduced amount of differentiable computations.
Due to the appearance of a neural network on the right-hand side of the equations of motion, the resulting satellite dynamics is governed by a NeuralODE, a neural Ordinary Differential Equation, characterized by its fully differentiable nature, allowing the derivation of variational equations (hence of the state transition matrix) and facilitating its use in connection to advanced numerical techniques such as Taylor-based numerical propagation and differential algebraic techniques. Efficient training of the network parameters occurs through two distinct approaches.
In this repository, you will find the code to train, analyze, and use thermoNETs for downstream tasks: including orbit propagation and neuralODE training. If you are using thermoNETs as part of your research, teaching, or other activities, we would be grateful if you could cite our work and/or star the repository. For citation purposes, you can use the following BibTex entry:
@inproceedings{thermonets,
title = {NeuralODEs for VLEO simulations: Introducing thermoNET for Thermosphere Modeling},
author = {Izzo, Dario and Acciarini, Giacomo and Biscani, Francesco},
booktitle = {29th International Symposium on Space Flight Dynamics},
year = {2024},
url = {https://arxiv.org/abs/2405.19384}
}out.mp4
- represent thermospheric density empirical models via a lightweight neural network (only a few thousand parameters)
- neural ODE training to adjust trained architectures to match observed and/or simulated satellite data
- neural representation of NRLMSISE-00 and JB-08 (pre-trained and ready for use)
- tutorial on the use of thermoNET for pure inference (i.e., as a thermospheric density model), as well as during orbit propagation, and for neural ODE fix (see
notebooksfolder)
First, clone the repository:
git clone https://github.com/esa/thermonetsThen enter the repository and activate the conda environment:
cd thermonets
conda env create -f environment.ymlThen, the module should be ready to import...
import sys
sys.path.append('..')
import thermonets as tnTo run one of the two pre-trained thermoNETs (i.e., either the JB-08 or the NRLMSISE-00 ones) you can first define the needed inputs - these vary depending on the model trianed. In our case, we support NRLMSISE-00 and JB-08.
NRLMSISE-00 inputs needed are:
- altitude (in km)
- longitude (in radians, between 0 and 2*pi)
- latitude (in radians, between -pi/2 and pi/2)
- F10.7 and F10.7a indexes
- Ap index
- seconds in day
- day of year
whereas JB-08 inputs needed are:
- altitude (in km)
- longitude (in radians, between 0 and 2*pi)
- latitude (in radians, between -pi/2 and pi/2)
- F10.7 and F10.7a indexes
- S10.7 and S10.7a indexes
- M10.7 and M10.7a indexes
- Y10.7 and Y10.7a indexes
- dDst/dT index
- seconds in day
- day of year
An example of an input preparation is as follows:
import sys
sys.path.append('..')
import thermonets as tn
import datetime
import numpy as np
date=datetime.datetime(2019, 8, 8, 20, 34, 42, 272745)
############### NRLMSISE-00 and JB-08 inputs ###############
#geodetic altitude in km
hs=np.linspace(180.,1000.,300) #300 points in the 180-1,000 km range
#geodetic longitude in [0,360] degrees and latitude in [-90,90] degrees --> in radians
lons=np.deg2rad(300.)
lats=np.deg2rad(15.)
#the F10.7 solar proxy:
f107 = 164.2
f107a = 152.8
#let's extract the day of the year and seconds in day from the date:
doy = date.timetuple().tm_yday
sid = date.hour * 3600 + date.minute * 60 + date.second + date.microsecond / 1e6
############### NRLMISE-00 only, remaining inputs ###############
#the Ap index
ap=13.
############### JB-08 only, remaining inputs ###############
s107=172.6
s107a=153.8
m107=159.8
m107a=137.
y107=139.3
y107a=137.
#finally the geomagnetic parameter referring to Dst index variations with the temperature: dDst /dT
dDstdT=115.then the thermoNET model for NRLMSISE-00 and JB-08 models can be called by simply doing:
density_thermonet_nrlmsise00=tn.nrlmsise00_tn(hs=hs,
lons=lons,
lats=lats,
f107=f107,
f107a=f107a,
ap=ap,
doy=doy,
sid=sid,)
density_thermonet_jb08=tn.jb08_tn(hs=hs,
lons=lons,
lats=lats,
f107=f107,
f107a=f107a,
s107=s107,
s107a=s107a,
y107=y107,
y107a=y107a,
m107=m107,
m107a=m107a,
dDstdT=dDstdT,
doy=doy,
sid=sid,)NOTE that the output of the thermonet will be of shape NxMxL, where N is the length of the altitude vector, M is the length of the longitude vector, and L is the length of the latitude vector. Alternatively, floats can also be passed, and then the corresponding dimension will be equal to 1. The above shape for the thermoNET output for instance, is 300x1x1
The above produces the following density profiles as a function of the altitude:
The pre-trained models display very low errors w.r.t. their ground truth (i.e., NRLMSISE-00 and JB-08): usually in the order of between 1 and 3% mean absolute percentage error. This is a table extracted from our publication:
Check out our publication for a more thorough discussion!
This repository open-sources two pre-trained thermoNET (one on the NRLMSISE-00 empirical model, and one on JB-08). In order to train a thermoNET from scratch for these two models, you can follow the tutorials under notebooks/nrlmsise00_train.ipynb and noteboooks/jb08_train.ipynb. However, it is essential to first generate a database of points to train on. This can be done by doing for NRLMSISE-00:
cd scripts
python generate_nrlmsise00_db.py --n_lonlat_points 100 --min_height 180 --max_height 1000 --num_processes 1 --n_height_points 100and for JB-08:
cd scripts
python generate_jb08_db.py --n_lonlat_points 100 --min_height 180 --max_height 1000 --num_processes 1 --n_height_points 100where min_height, max_height are in km. This might take several minutes for many points (e.g. the above is for several million points).. if you want something faster, you can reduce either the n_lonlat_points or n_height_points points requested.
Check out our notebooks folder for plenty of tutorials! In particular:
notebooks/nrlmsise00_train.ipynbandnotebooks/jb08_train.ipynbfor how to train thermoNET on empirical modelsnotebooks/nrlmsise00_analysis.ipynbandnotebooks/jb08_analysis.ipynbfor how to perform inference, and compare the models w.r.t. their ground truth, with different metrics & cool plotsnotebooks/orbit_propagation_with_thermoNET.ipynbfor how they can be integrated within an orbit propagator, written with a Taylor-based integration scheme (this notebooks requiresheyoka.py)notebooks/neural_ODEs.ipynbfor an example of how to adjust thermoNETs parameters for matching a downstream task (in that case, for better matching some observed trajectory data) using the NeuralODE approach. In that notebook, we use a thermoNET trained on NRLMSISE-00 and ask to adjust its weights and biases so that it then matches the trajectory generated using JB-08 empirical model (considered as the target). The latter could be produced with any observed or simulated ground truth data, with the same setup.
- Dario Izzo (European Space Agency)
- Giacomo Acciarini (European Space Agency & Surrey Space Center)
- Francesco Biscani (European Space Agency)