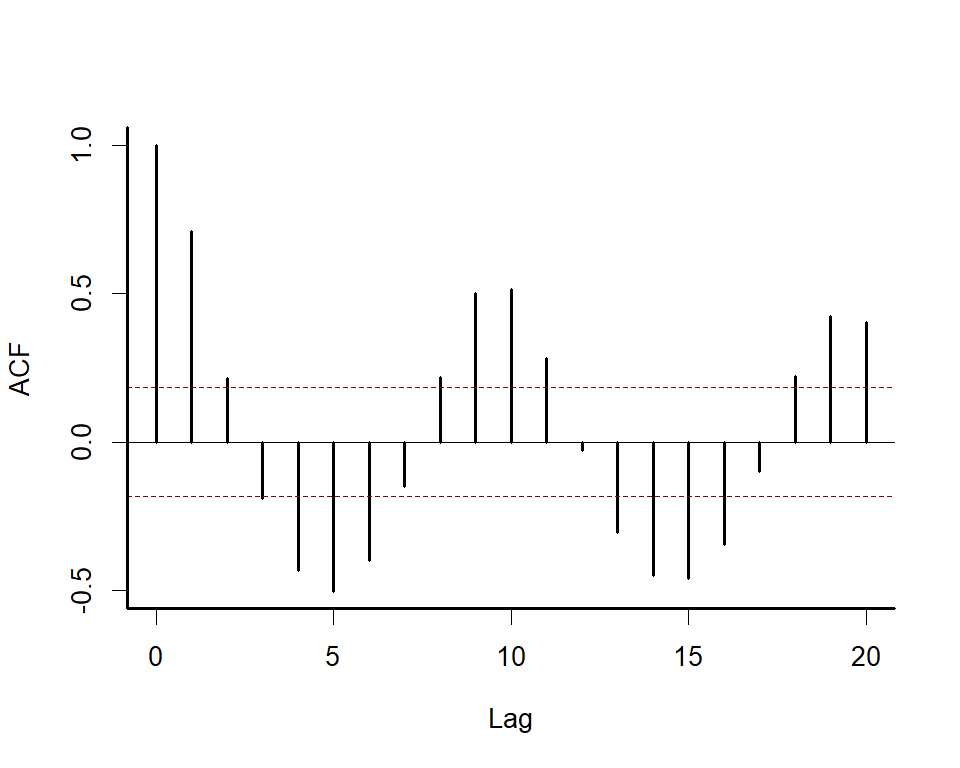The goal of mvgam is to fit Bayesian Dynamic Generalized Additive
Models to time series data. The motivation for the package is described
in Clark & Wells 2022 (published in Methods in
Ecology and Evolution), with additional inspiration on the use of
Bayesian probabilistic modelling coming from
Michael
Betancourt,
Michael Dietze and
Emily Fox,
among many others.
A series of vignettes cover data formatting, forecasting and several extended case studies of DGAMs. A number of other examples have also been compiled:
- mvgam case study 1: model comparison and data assimilation
- mvgam case study 2: multivariate models
- mvgam case study 3: distributed lag models
Install from GitHub using:
devtools::install_github("nicholasjclark/mvgam"). Note that to
condition models with MCMC sampling, either JAGS (along with packages
rjags and runjags) or Stan must be installed (along with either
rstan and/or cmdstanr). Please refer to installation links for
JAGS here, for Stan with rstan
here, or for Stan with cmdstandr
here. You
will need a fairly recent version of Stan to ensure all syntax is
recognized. If you see warnings such as
variable "array" does not exist, this is usually a sign that you need
to update Stan. We highly recommend you use Cmdstan through the
cmdstanr interface. This is because Cmdstan is easier to install, is
more up to date with new features, and uses less memory than Rstan.
See this documentation from the Cmdstan team
for more information.
When using any software please make sure to appropriately acknowledge the hard work that developers and maintainers put into making these packages available. Citations are currently the best way to formally acknowledge this work, so we highly encourage you to cite any packages that you rely on for your research.
When using mvgam, please cite the following:
- Clark, N.J. and Wells, K. (2022). Dynamic Generalized Additive Models (DGAMs) for forecasting discrete ecological time series. Methods in Ecology and Evolution. DOI: https://doi.org/10.1111/2041-210X.13974
As mvgam acts as an interface to Stan and JAGS, please
additionally cite whichever software you use for parameter estimation:
- Carpenter B., Gelman A., Hoffman M. D., Lee D., Goodrich B., Betancourt M., Brubaker M., Guo J., Li P., and Riddell A. (2017). Stan: A probabilistic programming language. Journal of Statistical Software. 76(1). 10.18637/jss.v076.i01
- Plummer, M. (2013). JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. Proceedings of the 3rd International Workshop on Distributed Statistical Computing. 124(125.10).
mvgam relies on several other R packages and, of course, on R
itself. To find out how to cite R and its packages, use the citation
function. There are some features of mvgam which specifically rely on
certain packages. The most important of these is the generation of data
necessary to estimate smoothing splines, which entirely rely on mgcv.
The rstan and cmdstanr packages together with Rcpp makes Stan
conveniently accessible in R, while the rjags and runjags packages
together with the coda package make JAGS accessible in R. If you
use some of these features, please also consider citing the related
packages.
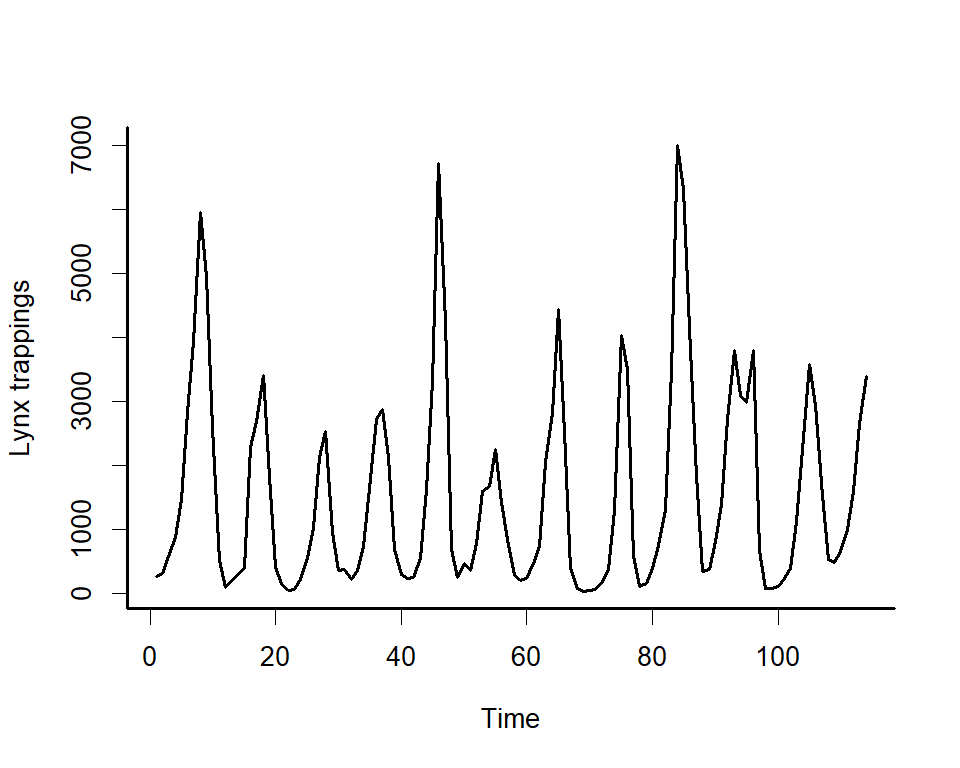
We can explore the model’s primary functions using a dataset that is
available with all R installations. Load the lynx data and plot the
series as well as its autocorrelation function
data(lynx)
lynx_full <- data.frame(year = 1821:1934,
population = as.numeric(lynx))
plot(lynx_full$population, type = 'l', ylab = 'Lynx trappings',
xlab = 'Time', bty = 'l', lwd = 2)
box(bty = 'l', lwd = 2)acf(lynx_full$population, main = '', bty = 'l', lwd = 2,
ci.col = 'darkred')
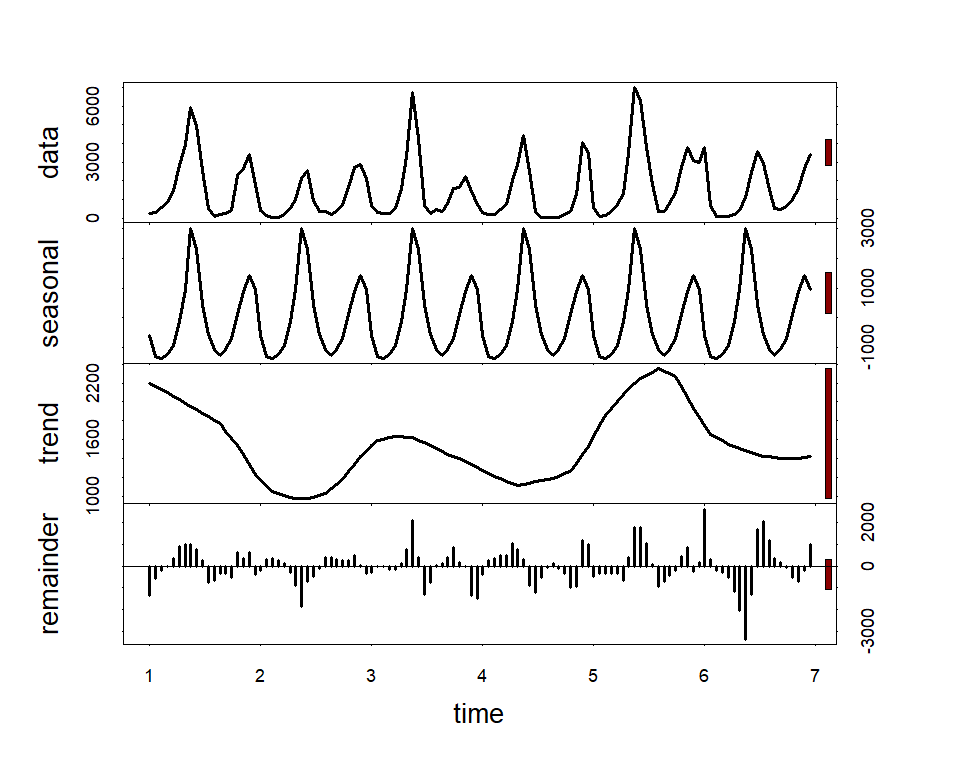
box(bty = 'l', lwd = 2)Along with serial autocorrelation, there is a clear ~19-year cyclic
pattern. Create a season term that can be used to model this effect
and give a better representation of the data generating process than we
would likely get with a linear model
plot(stl(ts(lynx_full$population, frequency = 19), s.window = 'periodic'),
lwd = 2, col.range = 'darkred')lynx_full$season <- (lynx_full$year%%19) + 1For mvgam models, we need an indicator of the series name as a
factor (if the column series is missing, this will be added
automatically by assuming that all observations are from a single time
series). A time column is needed to index time
lynx_full$time <- 1:NROW(lynx_full)
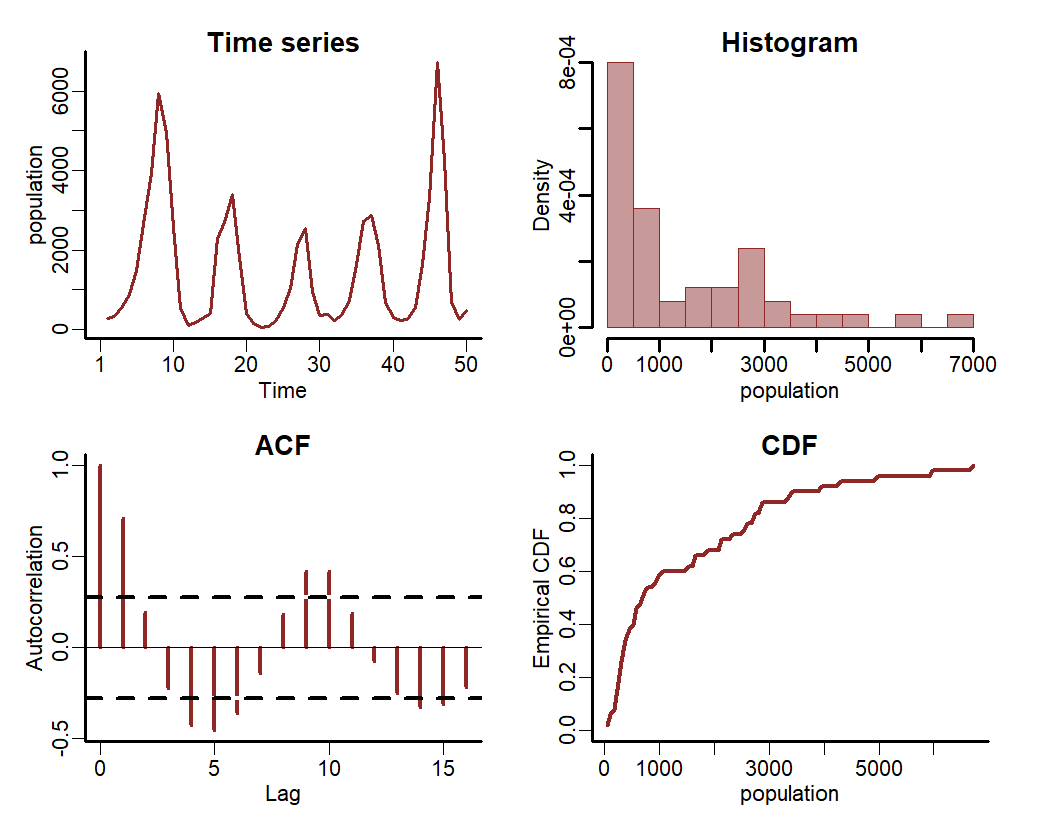
lynx_full$series <- factor('series1')Split the data into training (first 50 years) and testing (next 10 years of data) to evaluate forecasts
lynx_train = lynx_full[1:50, ]
lynx_test = lynx_full[51:60, ]Inspect the series in a bit more detail using mvgam’s plotting utility
plot_mvgam_series(data = lynx_train, y = 'population')Now we will formulate an mvgam model; this model fits a GAM in which a
cyclic smooth function for season is estimated jointly with a full
time series model for the temporal process (in this case an AR3
process). We assume the outcome follows a Poisson distribution and will
condition the model in Stan using MCMC sampling with the Cmdstan
interface:
lynx_mvgam <- mvgam(population ~ s(season, bs = 'cc', k = 12),
knots = list(season = c(0.5, 19.5)),
data = lynx_train,
newdata = lynx_test,
family = poisson(),
trend_model = AR(p = 3),
backend = 'cmdstanr')Inspect the Stan code for the model
code(lynx_mvgam)
#> // Stan model code generated by package mvgam
#> data {
#> int<lower=0> total_obs; // total number of observations
#> int<lower=0> n; // number of timepoints per series
#> int<lower=0> n_sp; // number of smoothing parameters
#> int<lower=0> n_series; // number of series
#> int<lower=0> num_basis; // total number of basis coefficients
#> vector[num_basis] zero; // prior locations for basis coefficients
#> matrix[total_obs, num_basis] X; // mgcv GAM design matrix
#> array[n, n_series] int<lower=0> ytimes; // time-ordered matrix (which col in X belongs to each [time, series] observation?)
#> matrix[10, 10] S1; // mgcv smooth penalty matrix S1
#> int<lower=0> n_nonmissing; // number of nonmissing observations
#> array[n_nonmissing] int<lower=0> flat_ys; // flattened nonmissing observations
#> matrix[n_nonmissing, num_basis] flat_xs; // X values for nonmissing observations
#> array[n_nonmissing] int<lower=0> obs_ind; // indices of nonmissing observations
#> }
#> parameters {
#> // raw basis coefficients
#> vector[num_basis] b_raw;
#>
#> // latent trend AR1 terms
#> vector<lower=-1.5, upper=1.5>[n_series] ar1;
#>
#> // latent trend AR2 terms
#> vector<lower=-1.5, upper=1.5>[n_series] ar2;
#>
#> // latent trend AR3 terms
#> vector<lower=-1.5, upper=1.5>[n_series] ar3;
#>
#> // latent trend variance parameters
#> vector<lower=0>[n_series] sigma;
#>
#> // latent trends
#> matrix[n, n_series] trend;
#>
#> // smoothing parameters
#> vector<lower=0>[n_sp] lambda;
#> }
#> transformed parameters {
#> // basis coefficients
#> vector[num_basis] b;
#> b[1 : num_basis] = b_raw[1 : num_basis];
#> }
#> model {
#> // prior for (Intercept)...
#> b_raw[1] ~ student_t(3, 6.5, 2.5);
#>
#> // prior for s(season)...
#> b_raw[2 : 11] ~ multi_normal_prec(zero[2 : 11],
#> S1[1 : 10, 1 : 10] * lambda[1]);
#>
#> // priors for AR parameters
#> ar1 ~ std_normal();
#> ar2 ~ std_normal();
#> ar3 ~ std_normal();
#>
#> // priors for smoothing parameters
#> lambda ~ normal(5, 30);
#>
#> // priors for latent trend variance parameters
#> sigma ~ student_t(3, 0, 2.5);
#>
#> // trend estimates
#> trend[1, 1 : n_series] ~ normal(0, sigma);
#> trend[2, 1 : n_series] ~ normal(trend[1, 1 : n_series] * ar1, sigma);
#> trend[3, 1 : n_series] ~ normal(trend[2, 1 : n_series] * ar1
#> + trend[1, 1 : n_series] * ar2, sigma);
#> for (s in 1 : n_series) {
#> trend[4 : n, s] ~ normal(ar1[s] * trend[3 : (n - 1), s]
#> + ar2[s] * trend[2 : (n - 2), s]
#> + ar3[s] * trend[1 : (n - 3), s], sigma[s]);
#> }
#> {
#> // likelihood functions
#> vector[n_nonmissing] flat_trends;
#> flat_trends = to_vector(trend)[obs_ind];
#> flat_ys ~ poisson_log_glm(append_col(flat_xs, flat_trends), 0.0,
#> append_row(b, 1.0));
#> }
#> }
#> generated quantities {
#> vector[total_obs] eta;
#> matrix[n, n_series] mus;
#> vector[n_sp] rho;
#> vector[n_series] tau;
#> array[n, n_series] int ypred;
#> rho = log(lambda);
#> for (s in 1 : n_series) {
#> tau[s] = pow(sigma[s], -2.0);
#> }
#>
#> // posterior predictions
#> eta = X * b;
#> for (s in 1 : n_series) {
#> mus[1 : n, s] = eta[ytimes[1 : n, s]] + trend[1 : n, s];
#> ypred[1 : n, s] = poisson_log_rng(mus[1 : n, s]);
#> }
#> }Have a look at this model’s summary to see what is being estimated. Note that no pathological behaviours have been detected and we achieve good effective sample sizes / mixing for all parameters
summary(lynx_mvgam)
#> GAM formula:
#> population ~ s(season, bs = "cc", k = 12)
#>
#> Family:
#> poisson
#>
#> Link function:
#> log
#>
#> Trend model:
#> AR(p = 3)
#>
#> N series:
#> 1
#>
#> N timepoints:
#> 50
#>
#> Status:
#> Fitted using Stan
#> 4 chains, each with iter = 1000; warmup = 500; thin = 1
#> Total post-warmup draws = 2000
#>
#>
#> GAM coefficient (beta) estimates:
#> 2.5% 50% 97.5% Rhat n_eff
#> (Intercept) 6.100 6.600 7.000 1.00 514
#> s(season).1 -0.600 0.033 0.670 1.00 941
#> s(season).2 -0.210 0.750 1.800 1.01 502
#> s(season).3 -0.045 1.100 2.400 1.01 435
#> s(season).4 -0.530 0.400 1.300 1.01 794
#> s(season).5 -1.200 -0.084 0.910 1.01 540
#> s(season).6 -0.970 0.046 1.000 1.00 605
#> s(season).7 -0.690 0.360 1.400 1.00 787
#> s(season).8 -0.900 0.190 1.800 1.01 437
#> s(season).9 -1.100 -0.320 0.730 1.00 544
#> s(season).10 -1.300 -0.660 0.031 1.00 837
#>
#> Approximate significance of GAM observation smooths:
#> edf Chi.sq p-value
#> s(season) 4.4 17441 0.26
#>
#> Latent trend AR parameter estimates:
#> 2.5% 50% 97.5% Rhat n_eff
#> ar1[1] 0.76 1.10 1.400 1.01 851
#> ar2[1] -0.84 -0.40 0.062 1.00 1553
#> ar3[1] -0.48 -0.14 0.310 1.01 624
#> sigma[1] 0.40 0.50 0.650 1.00 1571
#>
#> Stan MCMC diagnostics:
#> n_eff / iter looks reasonable for all parameters
#> Rhat looks reasonable for all parameters
#> 0 of 2000 iterations ended with a divergence (0%)
#> 0 of 2000 iterations saturated the maximum tree depth of 12 (0%)
#> E-FMI indicated no pathological behavior
#>
#> Samples were drawn using NUTS(diag_e) at Mon Nov 06 1:17:06 PM 2023.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split MCMC chains
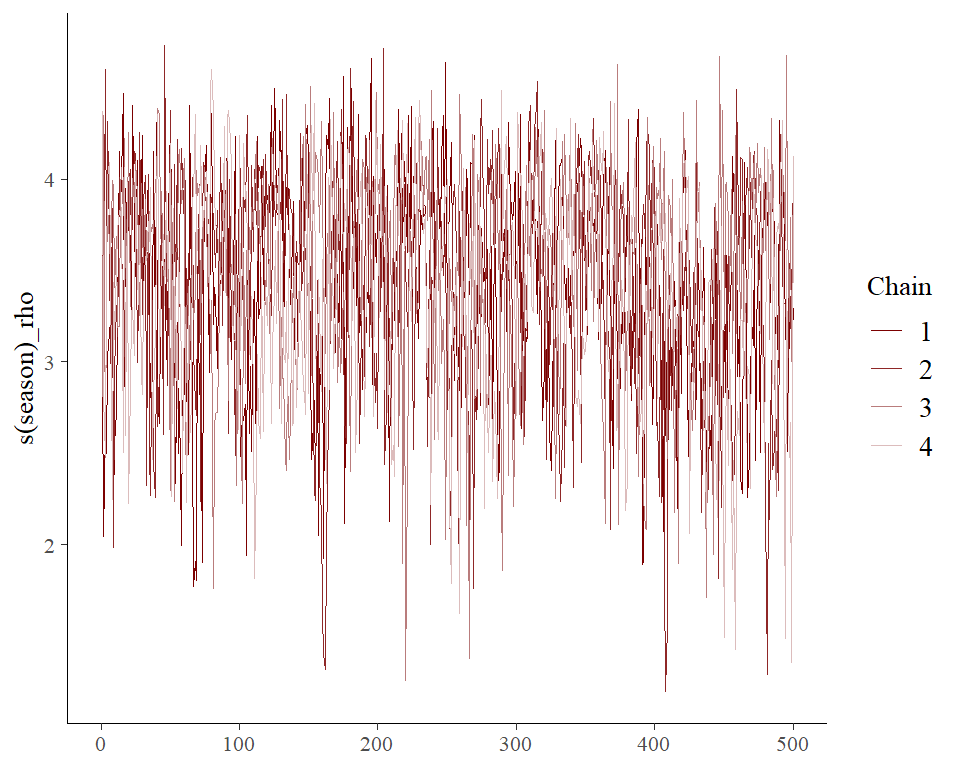
#> (at convergence, Rhat = 1)As with any MCMC software, we can inspect traceplots. Here for the
GAM smoothing parameters, using mvgam’s reliance on the excellent
bayesplot library:
mcmc_plot(lynx_mvgam, variable = 'rho', regex = TRUE, type = 'trace')
#> No divergences to plot.and for the latent trend parameters
mcmc_plot(lynx_mvgam, variable = 'trend_params', regex = TRUE, type = 'trace')
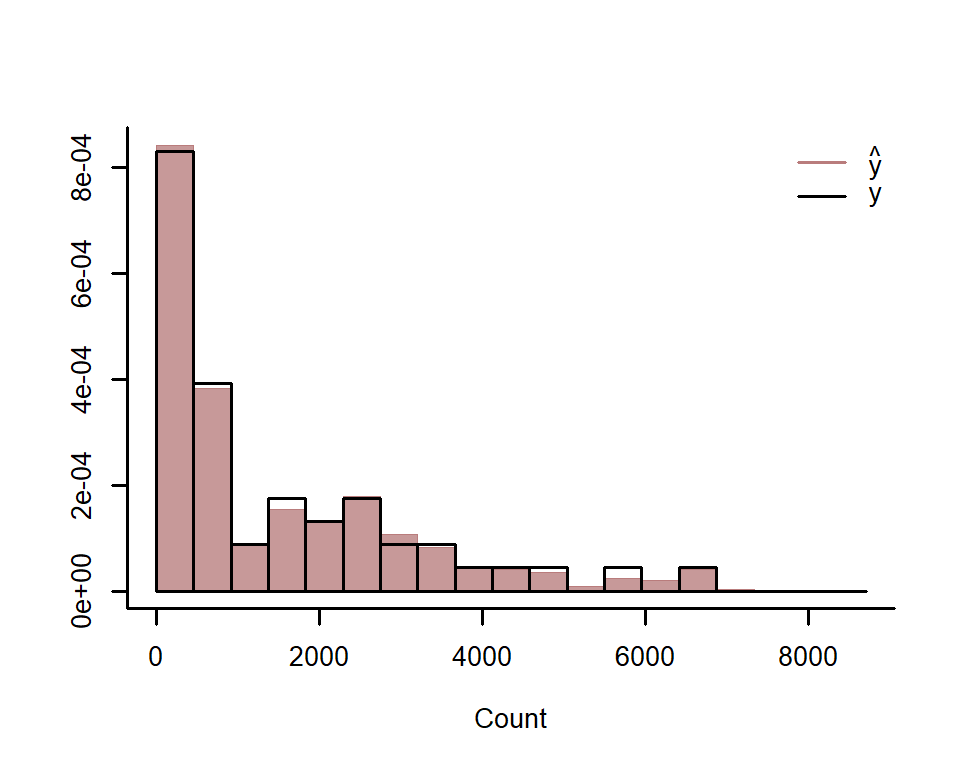
#> No divergences to plot.Use posterior predictive checks to see if the model can simulate data
that looks realistic and unbiased. First, examine histograms for
posterior retrodictions (yhat) and compare to the histogram of the
observations (y)
ppc(lynx_mvgam, series = 1, type = 'hist')Next examine simulated empirical Cumulative Distribution Functions (CDF) for posterior predictions
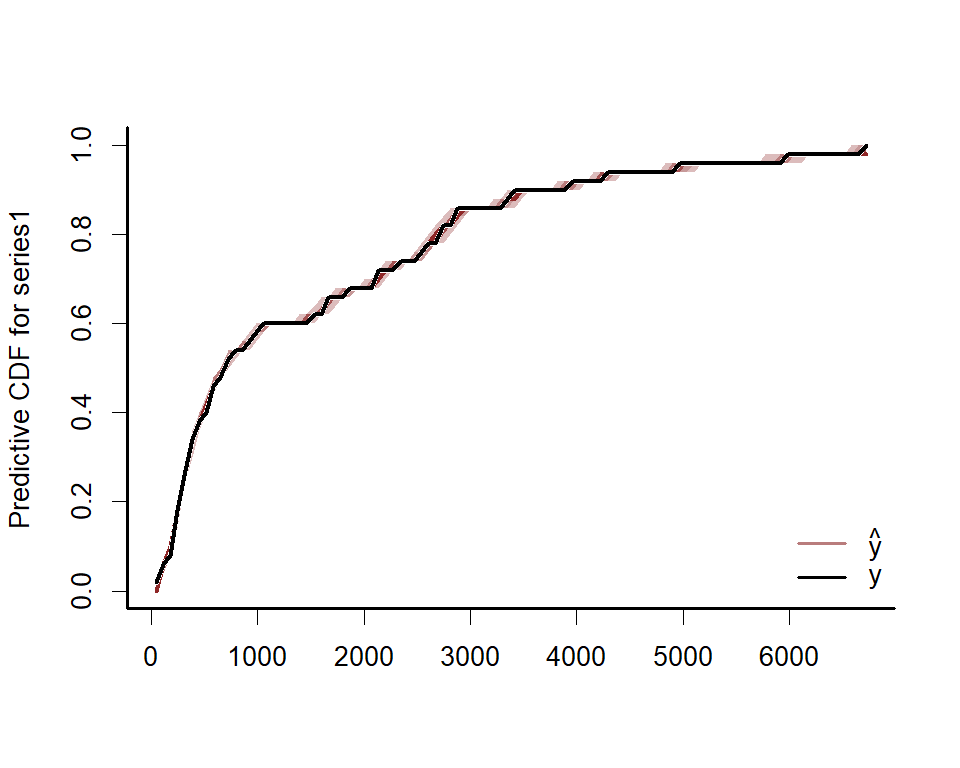
ppc(lynx_mvgam, series = 1, type = 'cdf')Rootograms are
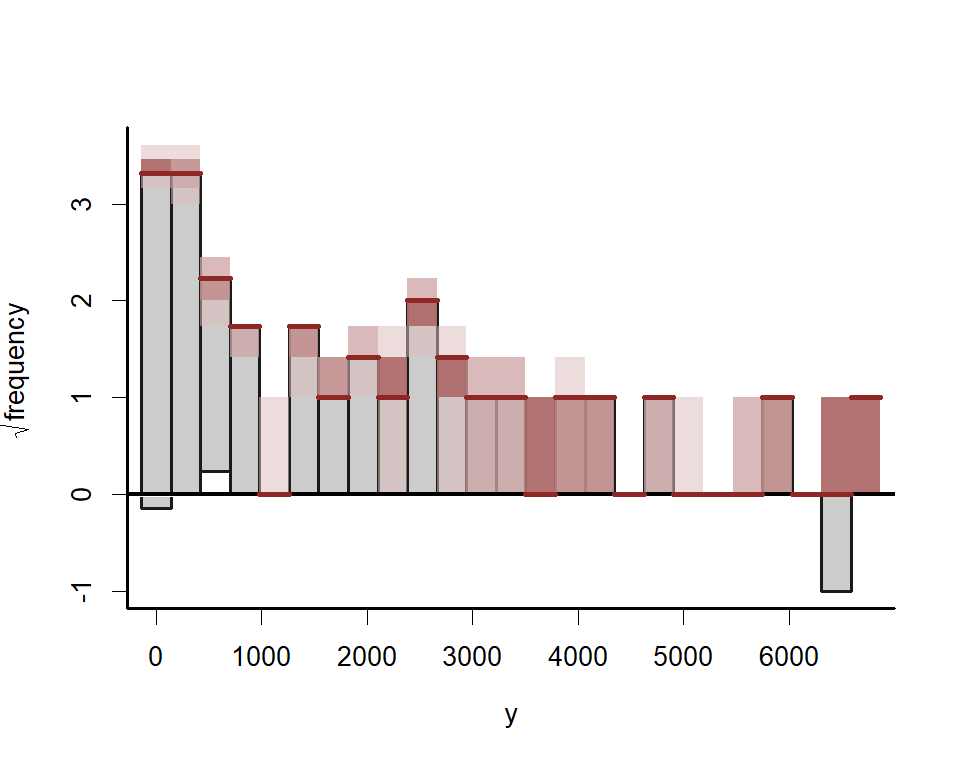
popular
graphical tools for checking a discrete model’s ability to capture
dispersion properties of the response variable. Posterior predictive
hanging rootograms can be displayed using the ppc() function. In the
plot below, we bin the unique observed values into 25 bins to prevent
overplotting and help with interpretation. This plot compares the
frequencies of observed vs predicted values for each bin. For example,
if the gray bars (representing observed frequencies) tend to stretch
below zero, this suggests the model’s simulations predict the values in
that particular bin less frequently than they are observed in the data.
A well-fitting model that can generate realistic simulated data will
provide a rootogram in which the lower boundaries of the grey bars are
generally near zero
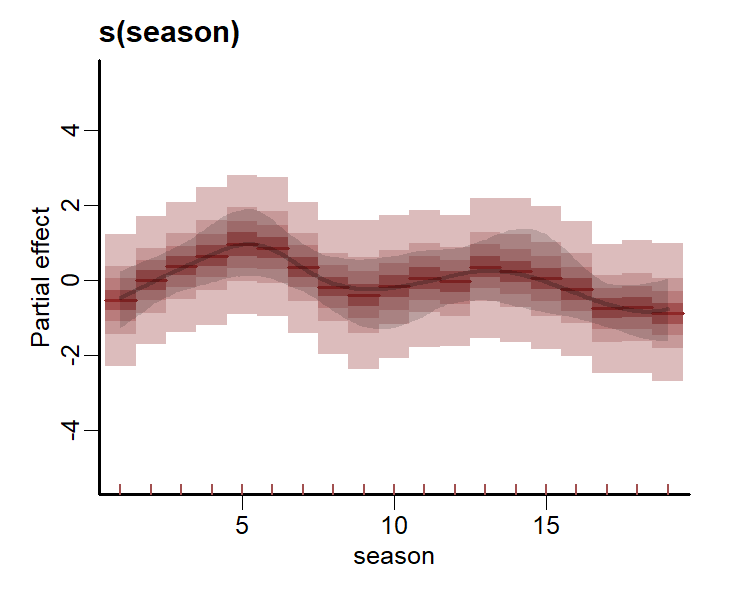
ppc(lynx_mvgam, series = 1, type = 'rootogram', n_bins = 25)All plots indicate the model is well calibrated against the training data. Inspect the estimated cyclic smooth, which is shown as a ribbon plot of posterior empirical quantiles. We can also overlay posterior quantiles of partial residuals (shown in red), which represent the leftover variation that the model expects would remain if this smooth term was dropped but all other parameters remained unchanged. A strong pattern in the partial residuals suggests there would be strong patterns left unexplained in the model if we were to drop this term, giving us further confidence that this function is important in the model
plot(lynx_mvgam, type = 'smooths', residuals = TRUE)First derivatives of smooths can be plotted to inspect how the slope of
the function changes. To plot these we use the more flexible
plot_mvgam_smooth() function
plot_mvgam_smooth(lynx_mvgam, series = 1,
smooth = 'season',
derivatives = TRUE)As for many types of regression models, it is often more useful to plot
model effects on the outcome scale. mvgam has support for the
wonderful marginaleffects package, allowing a wide variety of
posterior contrasts, averages, conditional and marginal predictions to
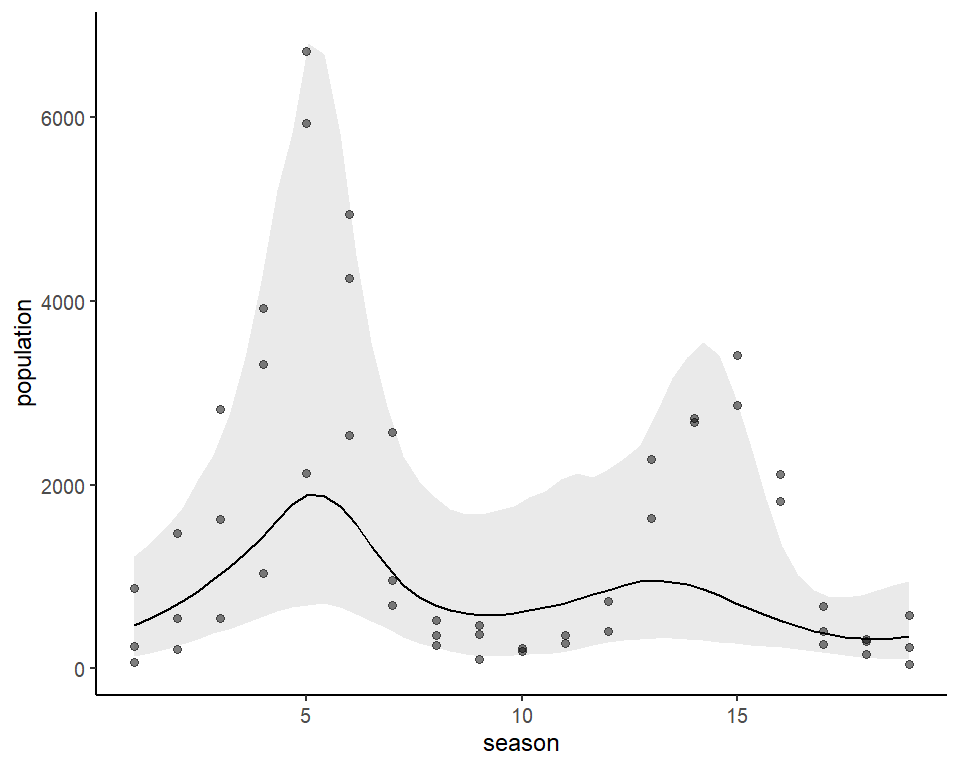
be calculated and plotted. Below is the conditional effect of season
plotted on the outcome scale, for example:
require(ggplot2)
#> Loading required package: ggplot2
plot_predictions(lynx_mvgam, condition = 'season', points = 0.5) +
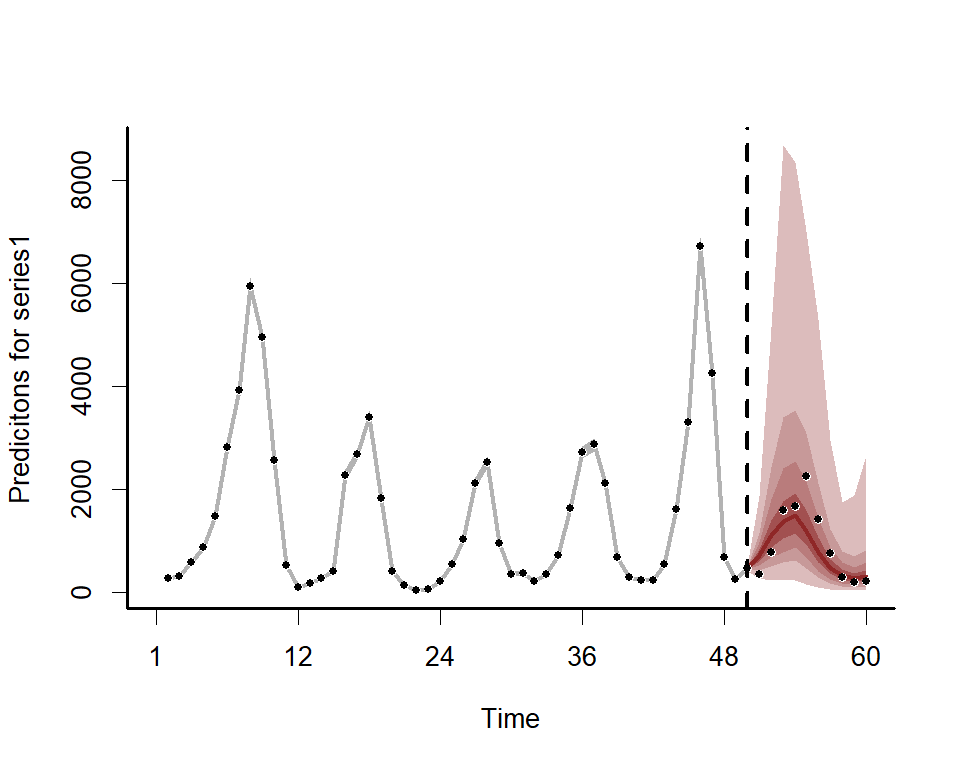
theme_classic()We can also view the mvgam’s posterior predictions for the entire
series (testing and training)
plot(lynx_mvgam, type = 'forecast', newdata = lynx_test)#> Out of sample CRPS:
#> [1] 2912.45
And the estimated latent trend component, again using the more flexible
plot_mvgam_...() option to show first derivatives of the estimated
trend
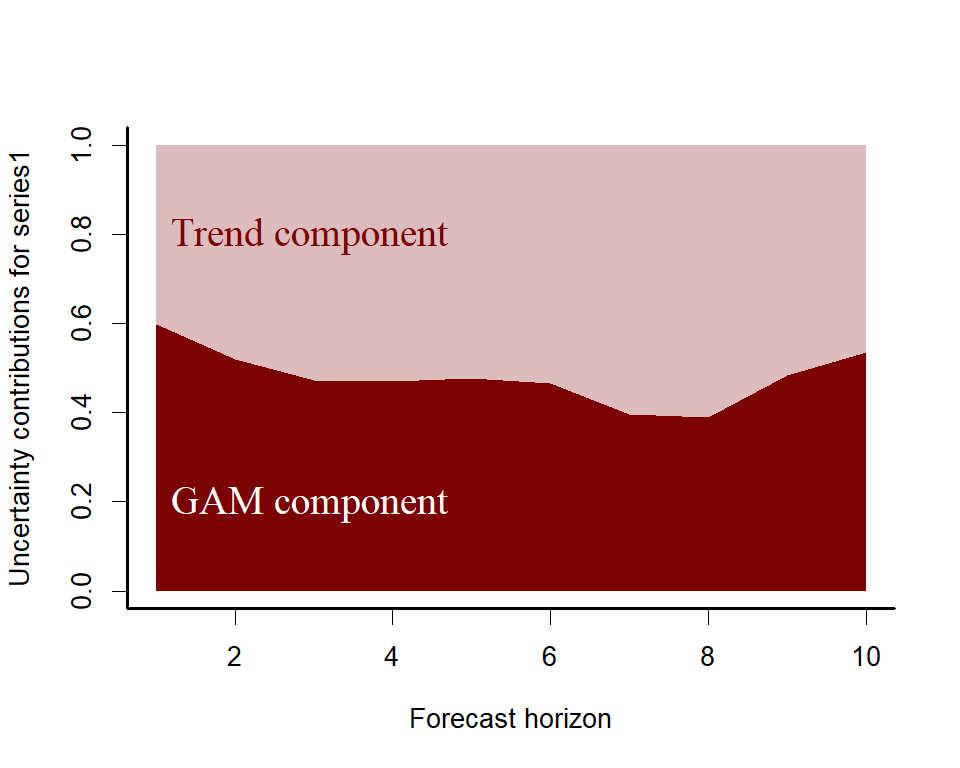
plot_mvgam_trend(lynx_mvgam, newdata = lynx_test, derivatives = TRUE)A key aspect of ecological forecasting is to understand how different components of a model contribute to
forecast uncertainty. We can estimate relative contributions to
forecast uncertainty for the GAM component and the latent trend
component using mvgam
plot_mvgam_uncertainty(lynx_mvgam, newdata = lynx_test, legend_position = 'none')
text(1, 0.2, cex = 1.5, label="GAM component",
pos = 4, col="white", family = 'serif')
text(1, 0.8, cex = 1.5, label="Trend component",
pos = 4, col="#7C0000", family = 'serif')Both components contribute to forecast uncertainty. Diagnostics of the
model can also be performed using mvgam. Have a look at the model’s
residuals, which are posterior empirical quantiles of Dunn-Smyth
randomised quantile residuals so should follow approximate normality. We
are primarily looking for a lack of autocorrelation, which would suggest
our AR3 model is appropriate for the latent trend
plot(lynx_mvgam, type = 'residuals')mvgam was originally designed to analyse and forecast non-negative
integer-valued data. These data are traditionally challenging to analyse
with existing time-series analysis packages. But further development of
mvgam has resulted in support for a growing number of observation
families. Currently, the package can handle data for the following:
gaussian()for real-valued datastudent_t()for heavy-tailed real-valued datalognormal()for non-negative real-valued dataGamma()for non-negative real-valued databetar()for proportional data on[0,1]poisson()for count datanb()for overdispersed count datatweedie()for overdispersed count data
Note that only poisson(), nb(), and tweedie() are available if
using JAGS. All families, apart from tweedie(), are supported if
using Stan. See ??mvgam_families for more information. Below is a
simple example for simulating and modelling proportional data with
Beta observations over a set of seasonal series with independent
Gaussian Process dynamic trends:
set.seed(100)
data <- sim_mvgam(family = betar(),
T = 80,
trend_model = 'GP',
prop_trend = 0.5,
seasonality = 'shared')
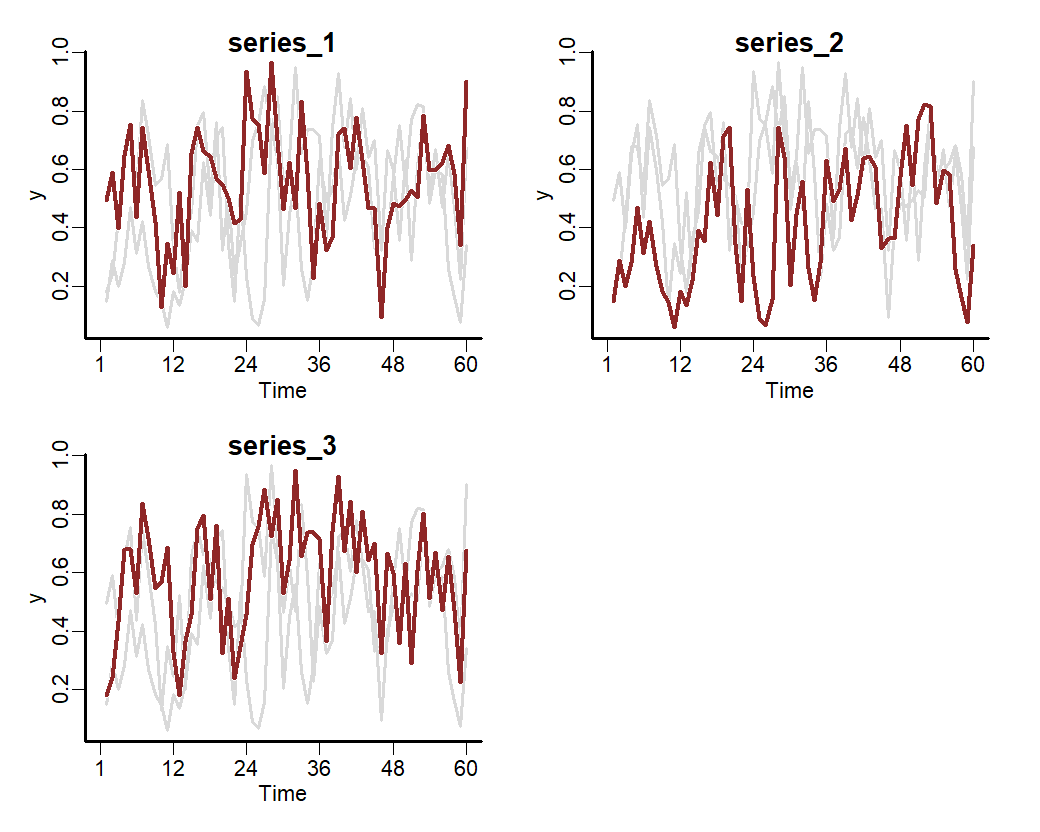
plot_mvgam_series(data = data$data_train, series = 'all')mod <- mvgam(y ~ s(season, bs = 'cc', k = 7) +
s(season, by = series, m = 1, k = 5),
trend_model = 'GP',
data = data$data_train,
newdata = data$data_test,
family = betar())Inspect the summary to see that the posterior now also contains
estimates for the Beta precision parameters
summary(mod, include_betas = FALSE)
#> GAM formula:
#> y ~ s(season, bs = "cc", k = 7) + s(season, by = series, m = 1,
#> k = 5)
#>
#> Family:
#> beta
#>
#> Link function:
#> logit
#>
#> Trend model:
#> GP
#>
#> N series:
#> 3
#>
#> N timepoints:
#> 60
#>
#> Status:
#> Fitted using Stan
#> 4 chains, each with iter = 1000; warmup = 500; thin = 1
#> Total post-warmup draws = 2000
#>
#>
#> Observation precision parameter estimates:
#> 2.5% 50% 97.5% Rhat n_eff
#> phi[1] 5.4 8.3 12 1 1780
#> phi[2] 5.8 8.8 13 1 1497
#> phi[3] 5.8 8.5 12 1 1845
#>
#> GAM coefficient (beta) estimates:
#> 2.5% 50% 97.5% Rhat n_eff
#> (Intercept) -0.23 0.18 0.44 1.01 665
#>
#> Approximate significance of GAM observation smooths:
#> edf Chi.sq p-value
#> s(season) 5.00 16.33 8.7e-06 ***
#> s(season):seriesseries_1 3.83 0.12 0.97
#> s(season):seriesseries_2 3.72 0.09 0.99
#> s(season):seriesseries_3 3.78 0.85 0.54
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Latent trend marginal deviation (alpha) and length scale (rho) estimates:
#> 2.5% 50% 97.5% Rhat n_eff
#> alpha_gp[1] 0.049 0.42 0.94 1.01 564
#> alpha_gp[2] 0.370 0.71 1.20 1.01 867
#> alpha_gp[3] 0.160 0.48 0.99 1.00 980
#> rho_gp[1] 1.200 3.70 13.00 1.01 491
#> rho_gp[2] 1.800 7.30 31.00 1.01 522
#> rho_gp[3] 1.400 4.70 21.00 1.00 760
#>
#> Stan MCMC diagnostics:
#> n_eff / iter looks reasonable for all parameters
#> Rhat looks reasonable for all parameters
#> 8 of 2000 iterations ended with a divergence (0.4%)
#> *Try running with larger adapt_delta to remove the divergences
#> 0 of 2000 iterations saturated the maximum tree depth of 12 (0%)
#> E-FMI indicated no pathological behavior
#>
#> Samples were drawn using NUTS(diag_e) at Mon Nov 06 1:18:24 PM 2023.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split MCMC chains
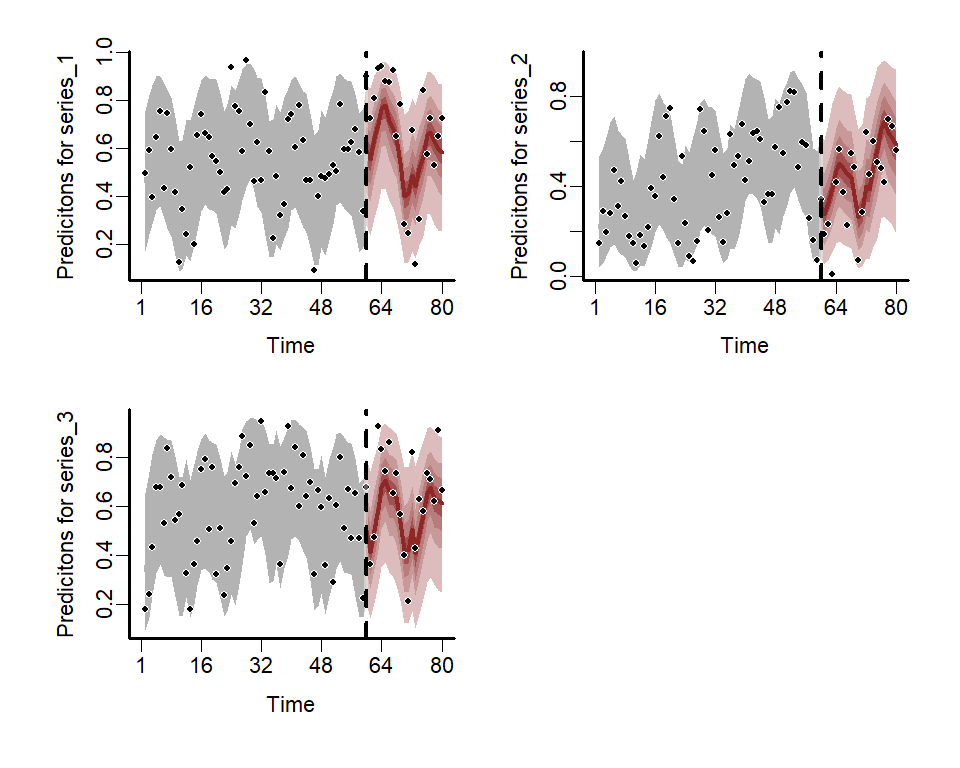
#> (at convergence, Rhat = 1)Plot the hindcast and forecast distributions for each series
layout(matrix(1:4, nrow = 2, byrow = TRUE))
for(i in 1:3){
plot(mod, type = 'forecast', series = i)
}#> Out of sample CRPS:
#> [1] 2.123262
#> Out of sample CRPS:
#> [1] 1.849232
#> Out of sample CRPS:
#> [1] 1.758914
There are many more extended uses of mvgam, including the ability to
fit hierarchical GAMs that include dynamic coefficient models, dynamic
factor and Vector Autoregressive processes. See the
package documentation for more details. The package
can also be used to generate all necessary data structures, initial
value functions and modelling code necessary to fit DGAMs using Stan
or JAGS. This can be helpful if users wish to make changes to the
model to better suit their own bespoke research / analysis goals. The
following resources can be helpful to troubleshoot:
This project is licensed under an MIT open source license