Geometry presents: the Groth16 Malleability Challenge

Preamble

Groth16 proofs are very popular and are used by many protocols in production. Libraries such as snarkjs and ark-groth do a good job abstracting proof systems and providing a nice interface for writing circuits. Nevertheless in order to write sound and safe protocols, it's very important to understand deeper cryptographic concepts.

The challenge

When learning about cryptographic protocols, it's extremely valuable to learn about potential attacks and problems, and the best way to learn is by attempting. To that end, Geometry Research is conducting The Groth16 Malleability Challenge. Any intrepid hackers who complete this challenge will earn a special NFT sponsored by Geometry. We provide a modified version of snarkjs which makes malleable proofs possible; your task is to modify a proof such that it remains valid but one of its public inputs differs.

Criteria

There is a challenge contract deployed at 0x4af905A972eab5020F965889EAd5bB4a20c1C2c3 on the Ethereum mainnet. It exposes a solve() function which accepts a Groth16 proof. The proof corresponds to the circuit described below. solve() will call a verifier function which will use the caller's Ethereum address as the first public input a.

If the verification passes, the contract will mint a non-transferable prize NFT to the caller.

The circuit

The circuit code can be found here: circuits/circuit.circom.

All zkey files are already in build/snark/circuit folder, so please do not build it again, as it will make it incompatible with the verifying key in the contract.

`snarkjs` modifications

This puzzle cannot be solved without tiny modifications to snarkjs. If you take a closer look in dependency section of package.json you'll see that this snarkjs fork is used and it only differs in one line:

diff --git a/build/main.cjs b/build/main.cjs
index 00e6965..ef1bd6f 100644
--- a/build/main.cjs
+++ b/build/main.cjs
@@ -4328,7 +4328,8 @@ async function newZKey(r1csName, ptauName, zkeyName, logger) {
             }
         }
 
-        for (let s = 0; s <= nPublic ; s++) {
+//         for (let s = 0; s <= nPublic ; s++) {
+        for (let s = 0; s < 1 ; s++) {
             const l1t = TAU_G1;
             const l1 = sG1*(r1cs.nConstraints + s);
             const l2t = BETATAU_G1;

That's correct — with a modification to only one line, malleable proofs can be crafted.

Submitting your proof

In src/solution.js there is a template for creating a malleable proof. You can run it with npm run solve. As expected, it fails, and your task will be to make it work.

Step 1: Make sure that the wallet address you put in:

const new_a = BigInt("PUT_YOUR_ADDRESS_HERE");

matches the address you plan to submit proof with!.

Step 2: Do some magic on proof such that script runs with no errors and you will get output like this:

[9033671481509310303480432375584986467146091997413160063526744094065848123115,1134048701020180641101291596483848464593285629853388726406614166877915275766,9735231883876420451920486462692839352481483823164847775245009097080002888605,18840452748006100068490126604883025783982577474616558019215463905727488555872,10499146114916491429815578549277100422153716639543017208844093487768363764387,7254171176247254130704409555297684571142738087816156016743992872816776219110,19434752999601924861048365747389278784362237409704016406266170338427127573370,2667505953663721770463958924381297083990119574041705395843873986309548427123]

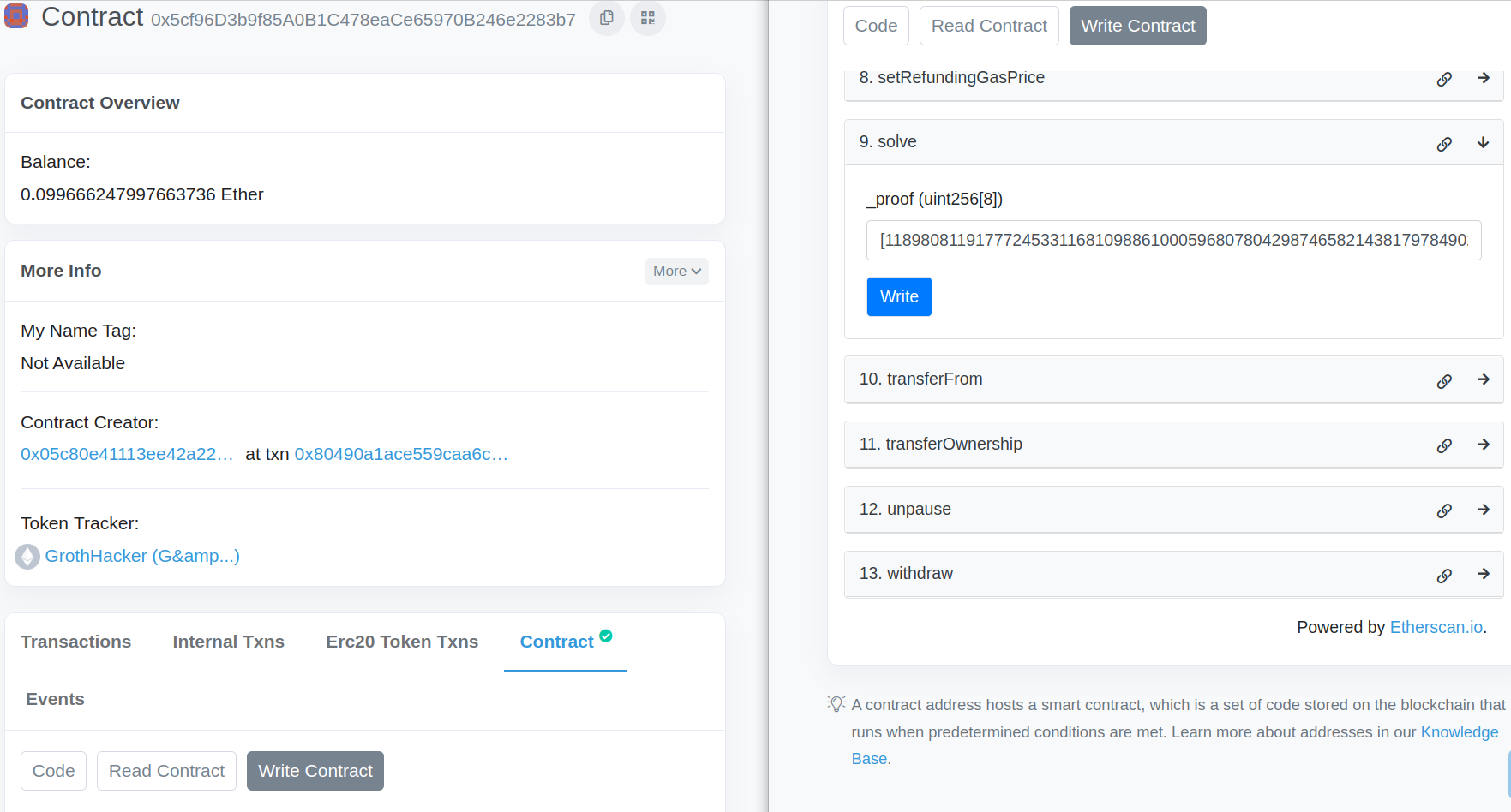
Next, navigate to the verifier contract page on Etherscan, connect your web3 wallet (using the account whose address is the first public input), and submit the above formatted proof to the solve() textbox. Click on "Write" to submit your transaction.

If your transaction succeeds, you will receive a non-transferable prize NFT. Congratulations!

Refund Policy

When you invoke the contract's solve() function via a transaction, the contract will provide a gas refund.

    // Perform the gas refund
    // 28521 was estimated using Remix
    uint256 gasSpent = gasBefore - gasleft() + 28521;
    address payable sender = payable(msg.sender);

    uint gaspice = tx.gasprice < refundingGasPrice ? tx.gasprice : refundingGasPrice;
    sender.transfer(gasSpent * gaspice);

Just make sure that gasprice you specify is no larger than refundingGasPrice in the contract. This is the upper bound that we are willing to refund. Please also note that if there is high volatility in gas prices, just be patient. We will make sure to adapt refundingGasPrice such that your transaction gets executed as quickly as possible.

eukadish/zkhack-groth-puzzle