Equi-normalization of Neural Networks

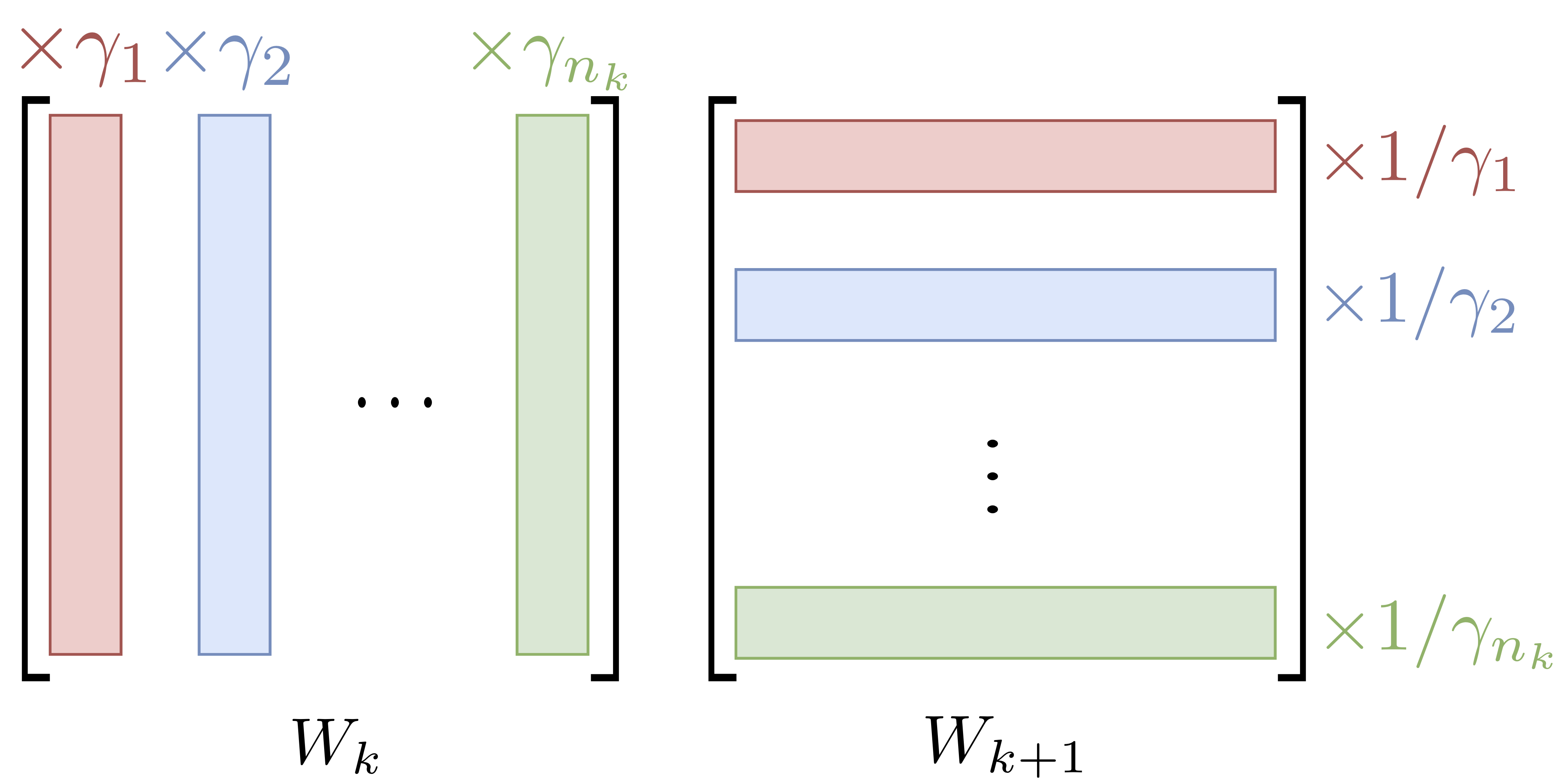
ENorm is a fast and iterative method for minimizing the L2 norm of the weights of a given neural network that provably converges to a unique solution. Interleaving ENorm with SGD during training improves the test accuracy.

This repository contains the implementation of ENorm as detailed in our paper Equi-normalization of Neural Networks (ICLR 2019). The library is easy to use and requires adding only two lines of code to your usual training loop.

$Matrices $W_k$ and $W_{k+1}$ are updated by multiplying the columns of the first matrix with rescaling coefficients. The rows of the second matrix are inversely rescaled to ensure that the product of the two matrices is unchanged. The rescaling coefficients are strictly positive to ensure functional equivalence when the matrices are interleaved with \mbox{ReLUs}. This rescaling is applied iteratively to each pair of adjacent matrices$

Dependencies

ENorm works with Python 3.6 and newest. To run the code, you must have the following packages installed:

NumPy
PyTorch (version>=0.4)

These dependencies can be installed with: pip install -r requirements.txt

How to use ENorm

The training procedure consists in performing one ENorm cycle (iterating ENorm on the entire network once) after each SGD step as detailed below.

from enorm import ENorm


# defining model and optimizer
model = ...
criterion = ...
optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9 weight_decay=1e-4)

# instantiating ENorm (here with asymmetric scaling coefficient c=1)
enorm = ENorm(model.named_parameters(), optimizer, c=1)

# training loop
for batch, target in train_loader:
  # forward pass
  output = model(input)
  loss = criterion(output, target)

  # backward pass
  optimizer.zero_grad()
  loss.backward()

  # SGD and ENorm steps
  optimizer.step()
  enorm.step()

Some precisions about the usage of ENorm (for details, see our paper):

ENorm is compatible with feedforward fully connected and/or convolutional architectures with ReLU and pooling layers.
The asymmetric scaling coefficient c penalizes the layers exponentially according to their depth. Usually, values of c equal to or slightly above 1 give the best results.
Currently, only the SGD optimizer is supported due to the momentum buffer update. Indeed, with using momentum, ENorm performs a jump in the parameter space, thus we update the momentum accordingly.
Optionally, one can perform more ENorm cycles or apply ENorm every k SGD iterations (k > 1). In our experience, performing one ENorm cycle after each SGD iteration generally works best.
In practice, we have found the training to be more stable when not balancing the biases.
When applying ENorm to a network with BatchNorm layers, we simply ignore the BatchNorm weights and perform the ENorm cycle on the network as usual.
Use the documentation of the file enorm.py file to adapt ENorm to your favourite network architecture.

Results

You can reproduce the results of our paper by running the following commands:

# fully connected network on CIFAR10 with 15 intermediary layers
python main.py --dataset cifar10 --model-type linear --n-layers 15 --enorm 0 --epochs 60 --lr 0.1 --weight-decay 1e-3 --momentum 0 --n-iter 5
python main.py --dataset cifar10 --model-type linear --n-layers 15 --enorm 1.2 --epochs 60 --lr 0.1 --weight-decay 1e-3 --momentum 0 --n-iter 5

# fully convolutional network on CIFAR10
python main.py --dataset cifar10 --model-type conv --enorm 0 --epochs 128  --lr 0.05 --weight-decay 1e-3 --momentum 0.9 --n-iter 5
python main.py --dataset cifar10 --model-type conv --enorm 1.1 --epochs 128 --lr 0.05 --weight-decay 1e-3 --momentum 0.9 --n-iter 5

License

ENorm is released under Creative Commons Attribution 4.0 International (CC BY 4.0) license, as found in the LICENSE file.

Bibliography

Please consider citing [1] if you found the resources in this repository useful.

[1] P. Stock, B. Graham, R. Gribonval and H. Jégou. Equi-normalization of Neural Networks.