Riemannian Convex Potential Maps

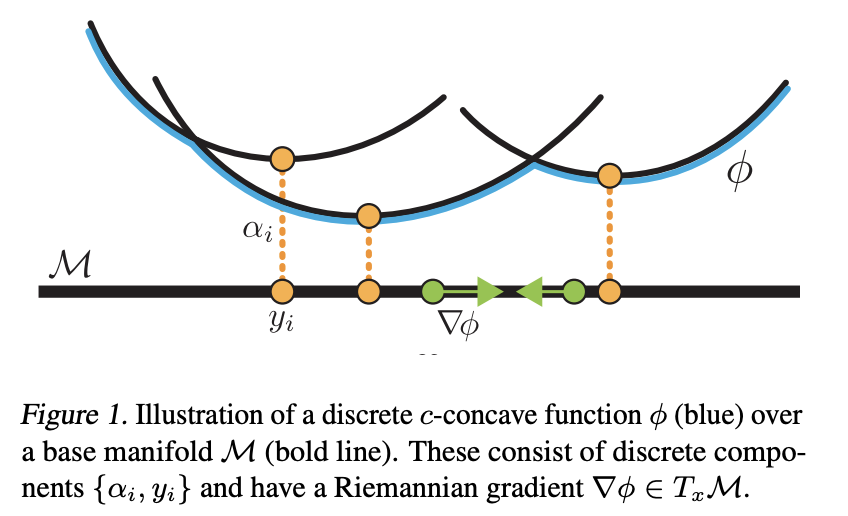
This repository is by Brandon Amos, Samuel Cohen and Yaron Lipman and contains the JAX source code to reproduce the experiments in our ICML 2021 paper on Riemannian Convex Potential Maps.

Modeling distributions on Riemannian manifolds is a crucial component in understanding non-Euclidean data that arises, e.g., in physics and geology. The budding approaches in this space are limited by representational and computational tradeoffs. We propose and study a class of flows that uses convex potentials from Riemannian optimal transport. These are universal and can model distributions on any compact Riemannian manifold without requiring domain knowledge of the manifold to be integrated into the architecture. We demonstrate that these flows can model standard distributions on spheres, and tori, on synthetic and geological data.

Reproducing our experiments

config.yaml contains the basic config for setting up our experiments. We currently use hydra 1.0.3. By default it contains the options to reproduce the multimodal sphere flow:

This can be run with:

$ ./main.py
workspace: /private/home/bda/repos/rcpm/exp_local/2021.06.21/053411
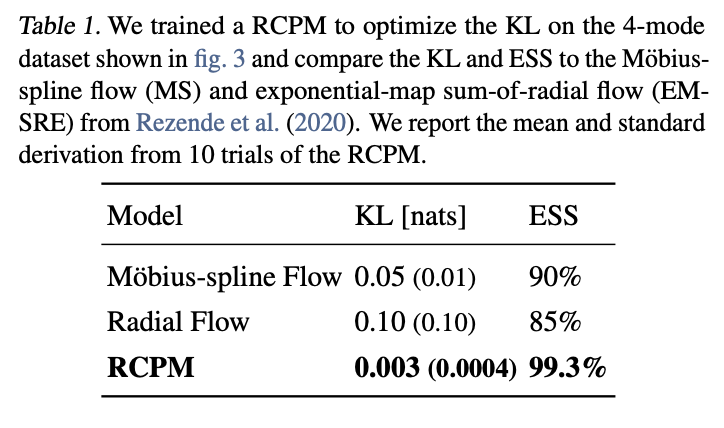
Iter 1000 | Loss -10.906 | KL 0.017 | ESS 96.74% | 9.54e-02s/it
Iter 2000 | Loss -10.908 | KL 0.013 | ESS 97.43% | 1.90e-02s/it
Iter 3000 | Loss -10.911 | KL 0.012 | ESS 97.71% | 1.75e-02s/it
Iter 4000 | Loss -10.912 | KL 0.010 | ESS 98.02% | 1.63e-02s/it
Iter 5000 | Loss -10.912 | KL 0.009 | ESS 98.19% | 1.46e-02s/it
...
Iter 30000 | Loss -10.915 | KL 0.006 | ESS 98.75% | 1.78e-02s/it

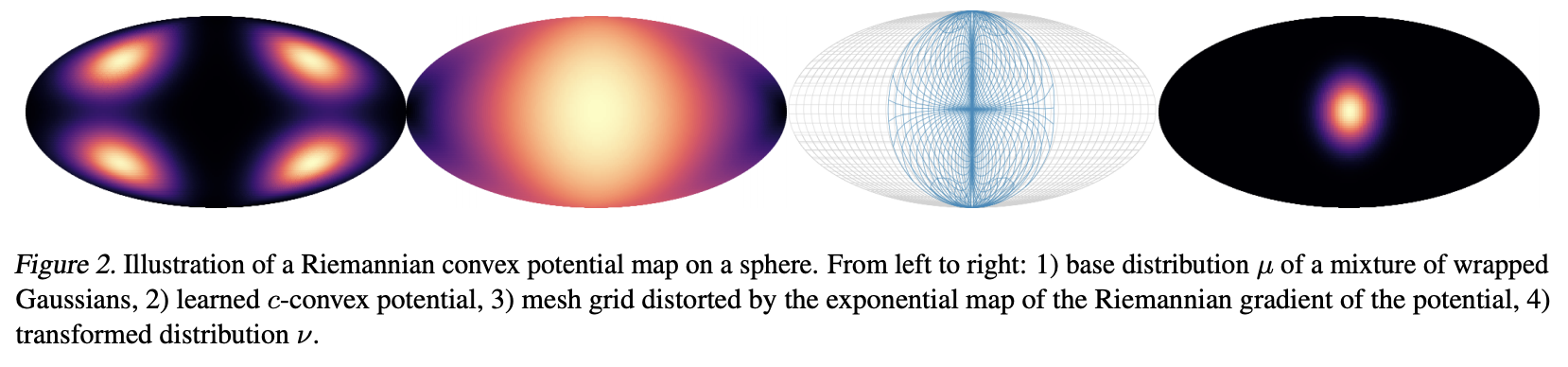
This will create a work directory in exp_local with the models and debugging information. You can use plot-components.py to further analyze the components of the learned flow, and plot-demo.py to produce the grid visualization from Figure 2 of our paper.

Training with the likelihood

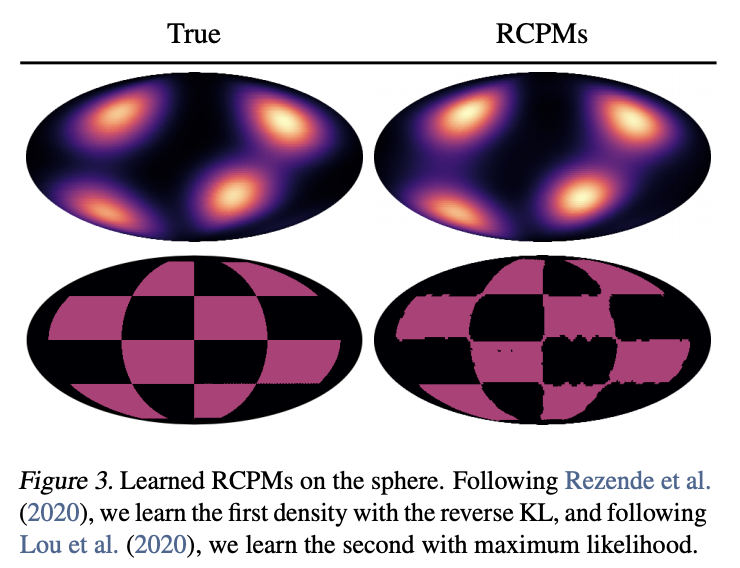
This can be done for the checkerboard dataset with:

$ ./main.py loss=likelihood base=SphereUniform target=SphereCheckerboard

Other JAX sphere flow library

katalinic/sdflows provides a great JAX re-implementation of Normalizing Flows on Tori and Spheres.

Citations

If you find this repository helpful for your publications, please consider citing our paper:

@inproceedings{cohen2021riemannian,
  title = {{Riemannian Convex Potential Maps}},
  author = {Cohen, Samuel and Amos, Brandon and Lipman, Yaron},
  booktitle = {Proceedings of the 38th International Conference on Machine Learning},
  pages = {2028--2038},
  year = {2021},
  editor = {Meila, Marina and Zhang, Tong},
  volume = {139},
  series = {Proceedings of Machine Learning Research},
  month = {18--24 Jul},
  publisher = {PMLR},
  pdf = {http://proceedings.mlr.press/v139/cohen21a/cohen21a.pdf},
  url = {https://proceedings.mlr.press/v139/cohen21a.html}
}

Licensing

This repository is licensed under the CC BY-NC 4.0 License.

facebookresearch/rcpm