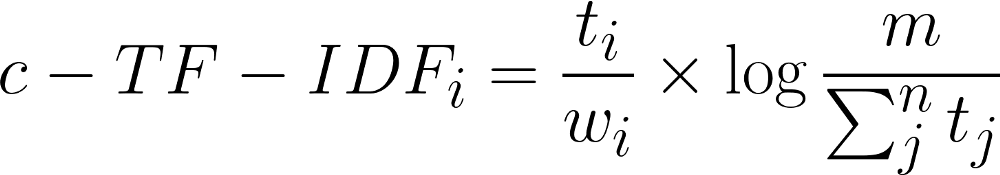c-TF-IDF is a class-based TF-IDF procedure that can be used to generate features from textual documents based on the class they are in.
Typical applications:
- Informative Words per Class: Which words make a class stand-out compared to all others?
- Class Reduction: Using c-TF-IDF to reduce the number of classes
- Semi-supervised Modeling: Predicting the class of unseen documents using only cosine similarity and c-TF-IDF
Corresponding TowardsDataScience post can be found here.
- About the Project
- Getting Started
2.1. Requirements
2.2. Basic Usage
2.3. Informative Words per Class
2.4. Class Reduction
2.5. Semi-supervised Modeling - c-TF-IDF
Fortunately, the requirements for this adaption is limited to numpy, scipy, pandas, and scikit-learn.
Basically your normal data stack which you can install with:
pip install -r requirements.txt
import pandas as pd
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
from ctfidf import CTFIDFVectorizer
# Get data and create documents per label
newsgroups = fetch_20newsgroups(subset='train', remove=('headers', 'footers', 'quotes'))
docs = pd.DataFrame({'Document': newsgroups.data, 'Class': newsgroups.target})
docs_per_class = docs.groupby(['Class'], as_index=False).agg({'Document': ' '.join})
# Create c-TF-IDF
count = CountVectorizer().fit_transform(docs_per_class.Document)
ctfidf = CTFIDFVectorizer().fit_transform(count, n_samples=len(docs))What makes c-TF-IDF unique compared to TF-IDF is that we can adopt it such that we can search for words that make up certain classes. If we were to have a class that is marked as space, then we would expect to find space-related words, right? To do this, we simply extract the c-TF-IDF matrix and find the highest values in each class:
import pandas as pd
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
from ctfidf import CTFIDFVectorizer
# Get data
newsgroups = fetch_20newsgroups(subset='train', remove=('headers', 'footers', 'quotes'))
docs = pd.DataFrame({'Document': newsgroups.data, 'Class': newsgroups.target})
docs_per_class = docs.groupby(['Class'], as_index=False).agg({'Document': ' '.join})
# Create bag of words
count_vectorizer = CountVectorizer().fit(docs_per_class.Document)
count = count_vectorizer.transform(docs_per_class.Document)
words = count_vectorizer.get_feature_names()
# Extract top 10 words
ctfidf = CTFIDFVectorizer().fit_transform(count, n_samples=len(docs)).toarray()
words_per_class = {newsgroups.target_names[label]: [words[index] for index in ctfidf[label].argsort()[-10:]] for label in docs_per_class.Class}Now that we have extracted the words per class, we can inspect the results:
words_per_class["sci.space"]
['mission',
'moon',
'earth',
'satellite',
'lunar',
'shuttle',
'orbit',
'launch',
'nasa',
'space']To me, it clearly shows words related to the category sci.space!
At times, having many classes can be detrimental to clear analyses. You might want a more general overview to get a feeling of the major classes in the data. Fortunately, we can use c-TF-IDF to reduce the number of classes to whatever value you are looking for. We can do this by comparing the c-TF-IDF vectors of all classes with each other in order to merge the most similar classes:
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_20newsgroups
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.feature_extraction.text import CountVectorizer
from ctfidf import CTFIDFVectorizer
# Get data and create documents per label
newsgroups = fetch_20newsgroups(subset='train', remove=('headers', 'footers', 'quotes'))
docs = pd.DataFrame({'Document': newsgroups.data, 'Class': newsgroups.target})
docs_per_class = docs.groupby(['Class'], as_index=False).agg({'Document': ' '.join})
# Create c-TF-IDF
count = CountVectorizer().fit_transform(docs_per_class.Document)
ctfidf = CTFIDFVectorizer().fit_transform(count, n_samples=len(docs))
# Get similar categories
distances = cosine_similarity(ctfidf, ctfidf)
np.fill_diagonal(distances, 0)
result = pd.DataFrame([(newsgroups.target_names[index], newsgroups.target_names[distances[index].argmax()])
for index in range(len(docs_per_class))],
columns=["From", "To"])The result shows which categories are most similar to each other and therefore which could be merged:
>>> result.head(5).values.tolist()
[['alt.atheism', 'soc.religion.christian'],
['comp.graphics', 'comp.windows.x'],
['comp.os.ms-windows.misc', 'comp.sys.ibm.pc.hardware'],
['comp.sys.ibm.pc.hardware', 'comp.sys.mac.hardware'],
['comp.sys.mac.hardware', 'comp.sys.ibm.pc.hardware']]This definitely seems to make sense! Combining christian with atheism and pc hardware with mac hardware.
Using c-TF-IDF we can even perform semi-supervised modeling directly without the need for a predictive model. We start by creating a c-TF-IDF matrix for the train data. The result is a vector per class which should represent the content of that class. Finally, we check, for previously unseen data, how similar that vector is to that of all categories:
import numpy as np
import pandas as pd
from sklearn import metrics
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.datasets import fetch_20newsgroups
from sklearn.metrics.pairwise import cosine_similarity
from ctfidf import CTFIDFVectorizer
# Get train data
train = fetch_20newsgroups(subset='train', remove=('headers', 'footers', 'quotes'))
docs = pd.DataFrame({'Document': train.data, 'Class': train.target})
docs_per_class = docs.groupby(['Class'], as_index=False).agg({'Document': ' '.join})
# Create c-TF-IDF based on the train data
count_vectorizer = CountVectorizer().fit(docs_per_class.Document)
count = count_vectorizer.transform(docs_per_class.Document)
ctfidf_vectorizer = CTFIDFVectorizer().fit(count, n_samples=len(docs))
ctfidf = ctfidf_vectorizer.transform(count)
# Predict test data
test = fetch_20newsgroups(subset='test', remove=('headers', 'footers', 'quotes'))
count = count_vectorizer.transform(test.data)
vector = ctfidf_vectorizer.transform(count)
distances = cosine_similarity(vector, ctfidf)
prediction = np.argmax(distances, 1)The results can be extracted with a simple classification report in scikit-learn:
>>> metrics.classification_report(test.target, prediction, target_names=test.target_names)
precision recall f1-score support
alt.atheism 0.21 0.59 0.31 319
comp.graphics 0.53 0.63 0.58 389
comp.os.ms-windows.misc 0.00 0.00 0.00 394
comp.sys.ibm.pc.hardware 0.54 0.53 0.54 392
comp.sys.mac.hardware 0.61 0.60 0.60 385
comp.windows.x 0.77 0.60 0.67 395
misc.forsale 0.60 0.66 0.63 390
rec.autos 0.63 0.67 0.65 396
rec.motorcycles 0.85 0.58 0.69 398
rec.sport.baseball 0.76 0.63 0.69 397
rec.sport.hockey 0.91 0.39 0.55 399
sci.crypt 0.83 0.51 0.63 396
sci.electronics 0.46 0.49 0.48 393
sci.med 0.56 0.59 0.58 396
sci.space 0.83 0.51 0.63 394
soc.religion.christian 0.62 0.62 0.62 398
talk.politics.guns 0.57 0.54 0.56 364
talk.politics.mideast 0.39 0.57 0.46 376
talk.politics.misc 0.18 0.31 0.23 310
talk.religion.misc 0.20 0.23 0.22 251
accuracy 0.52 7532
macro avg 0.55 0.51 0.52 7532
weighted avg 0.57 0.52 0.53 7532Although we can see that the results are nothing to write home about with an accuracy of roughly 50%… The accuracy is much better than randomly guessing the class which is 5%. Without any complex predictive model, we managed to get decent accuracy with a fast and relatively simple model. We did not even preprocess the data!
The goal of the class-based TF-IDF is to supply all documents within a single class with the same class vector. In order to do so, we have to start looking at TF-IDF from a class-based point of view instead of individual documents.
If documents are not individuals, but part of a larger collective, then it might be interesting to actually regard them as such by joining all documents in a class together.
The result would be a very long document that is by itself not actually readable. Imagine reading a document consisting of 10 000 pages!
However, this allows us to start looking at TF-IDF from a class-based perspective.
Then, instead of applying TF-IDF to the newly created long documents, we have to take into account that TF-IDF will take the number of classes instead of the number of documents since we merged documents. All these changes to TF-IDF results in the following formula:
Where the frequency of each word t is extracted for each class i and divided by the total number of words w.
This action can be seen as a form of regularization of frequent words in the class.
Next, the total, unjoined, number of documents m is divided by the total frequency of word t across all classes n.