Just another Slice Sampler for Bayesian Sampling -- but highly efficient and flexible in pure R (i.e., no more weird JAGS/BUGS/STAN syntax ).
Why would you want a pure-R Gibbs Sampler (and specifically a "Slice Sampler") when JAGS/BUGs exists? We used this sampler in Rankin and Marsh, 2020 for a complex Bayesian analysis of Dugongs which could not be run in JAGS or STAN... we had missing data, complex mixture priors, and a hierarchical process that required a custom Gibbs sampler.
Our Slice Sampler (based on Neal 2003) worked so well, that I decided to open-source it for others.
Be sure to check out our examples in demos/. And be sure to read about the key-parameters below.
-
src/flexible_slice_sampler.R- source code with flexible slice sampler -
src/example_log-posteriors.R- some example log-posteriors to inspire you to craft your own log-posteriors -
demos/demo_multivariate_regression_with_student-t_priors.R- script to demonstrate sparse Bayesian regression using Student-T priors -- in comparison with the Lasso ($\ell_1$ -regularization) -
demos/demo_jags_vs_slice_zeroInflatedPoisson.R- script to compare JAGS, for a Zero-Inflated Poisson model -
demos/random-effects.R- script demonstrating random-effects and hierarchical models, and JAGS comparison, using a random-effects Poisson regression with half-student-t priors -
demos/demo_data-imputation.R- script demonstrating dynamic data imputation
You should use this flexibl R-based Slice Sampler for Bayesian analysis if:
- No 'rejection' sampling - don't waste compute-resources throwing out samples a la Metropolis-Hasting.
- Matrix Operations - these are cumbersome in JAGS but can be easy and optimized in R
-
Novel Distributions - if you need a distribution that is not supported in JAGS/BUGS/STAN
- whatever probability distribution you code in R, you can use in this Slice Sampler
-
Intractible Priors - you have an intractible Prior distribution (and likewise intractible posterior) that can't be normalized
- for example, one of our priors was a mixture distribution based on the outputs from another independent model. You can pipe-in any external info you want, so long as you can code-it in R and can sample from it with a
dfunction-type of log-density.
- for example, one of our priors was a mixture distribution based on the outputs from another independent model. You can pipe-in any external info you want, so long as you can code-it in R and can sample from it with a
-
Penalities on Derived Quantities - you want to calculate derived quantities, and place priors on them
- you want to penalize some quantity that is a derivative of your process-parameters
- e.g., in ecology's mark-recapture, we often have prior information on derivatives of our statistical models (like we know the population-size isn't 0 nor is it 10000) but these quantities are derivatives, often not direct parameters in our likelihood.
- regulation can also be thought-of as a penalty on derviative quantities (the
$\ell_1$ -norm of parameters). See the demos.
-
Missing Data Imputation - we can do subsampling or random-inputation, per MCMC iteration.
- changing the data is illegal in JAGS, but here we can flexibly subsample or impute the data for each MCMC iteration.
- because everything is R-based, you can run the slice sampler for a few iterations, then run a subsampling/imputation step outside the function, and then continue with the slice-sampler. This R-based Gibbs-routine opens-up lots of possibilities.
-
Interweave Complex Processes -you want to interweave complex R-processes in between vanilla MCMC
- e.g. let's say a part of your Gibbs-sampling depends on a Hidden-Markov-Model process that is unavailable in JAGS/BUGS, like sampling of HMM-states. You can sample from these states outside of the slice sampler using conventional HMM R-code, then run the Slice Sampler conditional on those states as "data", and repeat.
- BUGS/JAGS is annoying - why code in BUGS/JAGS if you can do it better & faster in R?
- Poor mixing in BUGS/JAGS - for random-effects models, the Flexible-R-SliceSampler mixes better and converges faster than BUGS/JAGS (see the random-effects models below).
- You have a simple model with simple data that is easily run in JAGS/BUGS
- You're unfamiliar with likelihoods and have difficulty making R-likelihood functions
In regards to the past point, each model/study will require its own likelihoood-functions and prior-functions, so you'll need to custom-write these functions anew every time. This may seem cumbersome, but it is the cost of being flexible.
Let's run a Zero-Inflated poisson model, with poisson variable lambda and zero-inflation variable psi. Let's say the data is simply: y <- c(1,0,0,0,10,0,3,0,0,0,0,0,0,30).
In JAGS, the model syntax would be:
jags_model_syntax <- "model{
# prior on psi
psi ~ dbeta(prior_psi_a,prior_psi_b)
# prior on (log)lambda
tau <- 1/(prior_lambda_sigma * prior_lambda_sigma)
loglambda ~ dnorm(prior_lambda_mean, tau)
lambda <- exp(loglambda)
# likelihood
for(i in 1:N){
# zero-inflation process:
zip[i] ~ dbern(psi)
# toggle-able lambda based on zero-inflation
lambda1[i] <- lambda*zip[i] + 0.000001
# .. NOTICE THE CONSTANT 0.000001 that is necessary to stabilize the ZIPpoisson!
# poisson likelihood
y[i] ~ dpois(lambda1[i])
}
}
"We will now re-write the above JAGS ZIPpoisson model using pure R-functions to run the slice.sample function. It is easy.
In particular, for each variable to sample (e.g. lambda and psi), we must write a log-posterior function that ingests the data, the prior parameters, and computes the log-likelihood at lambda=x and the log-prior-density at lambda=x. Importantly, the posteriors can be unnormalized, so we merely have to return the log-likelihood and log-prior-density at x.
Here are the log-posterior functions for lambda and psi, which correspond to the above JAGS/BUGS model. Notice that we make use of native R density functions like dnorm, dpois, etc.:
# log posterior with log-normal prior on `lambda` (the poisson process)
log_posterior_ziplambda <- function(x_target,
x_all,
data_likelihood,
prior_parameters
){
# data for likelihood: y values
y <- data_likelihood$y
# (naive) loglikelihood for zip poisson (works, but primariy for readability
likelihoods_poisson_unconditional <- dpois(y,lambda=x_all['lambda'],log=FALSE)
likelihoods_zip <- (1-x_all['psi'])*(y==0) + x_all['psi']*likelihoods_poisson_unconditional
loglike <- sum(log(likelihoods_zip))
# normal prior on log-lambda
log_prior <- dnorm(
log(x_target),
mean=prior_parameters[['prior_lambda_mean']],
sd=prior_parameters[['prior_lambda_sigma']], # note the sqrt(1/tau) for JAGS-compatibility,
log=TRUE
)
# return unnormalized posterior
return(loglike + log_prior)}
# log-posterior with Beta prior on `psi` (the zero-inflation parameter)
log_posterior_zippsi <- function(x_target,
x_all,
data_likelihood,
prior_parameters
){
# data for likelihood: y values
y <- data_likelihood$y
# (naive) loglikelihood
likelihoods_poisson_unconditional <- dpois(y,lambda=x_all['lambda'],log=FALSE)
likelihoods_zip <- (1-x_all['psi'])*(y==0) + x_all['psi']*likelihoods_poisson_unconditional
loglike <- sum(log(likelihoods_zip))
# logprior density on psi with Beta prior
log_prior <- dbeta(
x_target,
shape1=prior_parameters[['prior_psi_a']],
shape2=prior_parameters[['prior_psi_b']],
log=TRUE
)
# return unnormalized log-posterior
return(loglike + log_prior)}
# collect log-posterior functions in a named-list
list_of_log_posteriors = list(
"lambda" = log_posterior_ziplambda,
"psi" = log_posterior_zippsi
) Notice that each log-posterior density function must have the same arguments:
x_target: the candidate value of the variable for the posterior functionx_all: a named numeric variable with all variables in a vector, needed to compute the likelihood.data_likelihood: a named-list with all the data necessary to compute the likellihood (like the JAGS argumentdata)prior parameters: a named-list with the prior-parameters for each variable to sample
The log-posterior functions are collected in a named-list list_of_log_posteriors, with an entry for each variable to sample (lambda and psi). The list is passed as an argument slice.sample function.
samples_mcmc <- slice.sample(
x.init=c('lambda'=10, 'psi'=0.5), # initial estimates of variables
list_of_log_posteriors, # list of log-posterior densities per variable
data_likelihood, # y data and model-matrices
prior_parameters_list, # hyperparameters for priors
nslice=4000, # number of slices
x.lowb=c(0.000001,0.0000001), # lower safety bounds on variables
x.uppb=c(60,0.9999999), # upper safety bounds on variables
w=c(5, 0.3), # W hyperparameter governing Slice Sampler (see Details)
m=10, # number of steps of W (see Details)
)Read below for more about the other arguments of slice.sample. Or, have a look at the following demo files.
Neal (2003) describes a rejection-free method of MCMC sampling for complex multivariate joint-posteriors. _Slice-Sampling also has relatively few "tunable" hyperparameters, unlike some Metropolis-Hastings-like methods that fail to converge if the hyperparameters are poorly set.
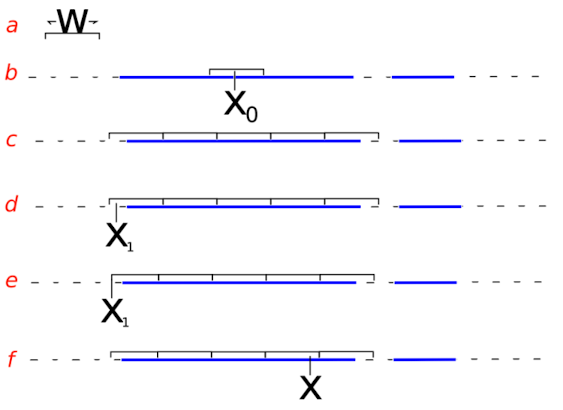
The most important hyperparameter is the STEP-SIZE parametre W -- it is used to laterally "step" arond the univariate-parameter interval of x to find good regions of the posterior-density to sample x. You'll need to read Neal 2003 to get a better understanding.
In Flexible-R-SliceSampler, we have a good method of automatically adjusting the step-size W parameters. However, the W parameters must be carefully watched to ensure they converge on acceptable values, and the sampler doesn't hang, choke, or mix badly.
Usually, if the W step-sizes don't converge, there is something else wrong with the model.
Given a point
- sample
$z$ uniformly along vertical from 0 to f(x):$z\sim\mathcal{U}(0,f(x))$ - find the left-most point (
$L$ ) at which$f(L) = z$ - find the right-most point (
$R$ ) at which$f(R) = z$ - sample a new
$x_{\text{new}}$ uniformly between$L$ and$R$ :$x_{\text{new}}\sim\mathcal{U}(L,R)$ - If
$f(x_{\text{new}}) > z$ then accept$x = x_{\text{new}}$ , and move-on to next variable - If not then "shrink" the boundaries L and R:
- If
$x_{\text{new}} < x$ , then$L \leftarrow x_{\text{new}}$ - Elif
$x_{\text{new}} > x$ , then$R \leftarrow x_{\text{new}}$ - Repeat steps 4 to 6 until
$f(x_{\text{new}}) > z$
- If
Notice there is some hand-waiving for the steps 2 & 3 ("find the left-most point (
The critical point: the user must supply a reasonable value for the slice.sample has an automatic way to adjust W once the sampling gets going.
| 📝 | We have found that the best step-size (W) is the long-run average of R-L over the entire density. Therefore, during sampling, we can monitor R and L, and slowly adjust W to the long-run average of R-L |
|---|
The core function is slice.sample in src/flexible_slice_sampler.R. We now go over the key arguments.
x.init- initial estimates of all variableslist_of_log_posteriors- named-list with the log-posterior density function, for each variable to sample.data_likelihood- a list with the data for likelihood; this data will be based to each function in list_of_log_posteriors.prior_parameters_list- a named-list with prior-parameters, for each variable to samplenslice- number of MCMC iterations (no thinning)x.lowb- numeric vector of lower-bound values forx.initx.uppb- numeric vector of upper-bound values forx.initw- numeric vector for step-size intervals for each x to sample (key parameter to set)m- max number of steps to shift left or rightw_auto_adjust=TRUE- whether to auto-adjustw, if FALSE, thenwis fixedw_auto_adjust_factor=0.8- a decay factor to slowly harden the auto-adjusted estimates ofw
You'll need to custom-code the list_of_log_posteriors, and the data_likelihood, and priors in prior_parameters_list.
You're ability to parameterize the data and priors should be obvious. The difficult part will be to custom-codie the log-posteriors, but if you can do it in JAGS/BUGS, you should be able to do so much easier in native-R for the log posteriors.
See example log-posteriors in src/example_log-posteriors.R
See demo-examples how to use the slice.sample function in the demo files (like demo/demo_multivariate_regression_with_student-t_priors.R and demo/demo_jags_vs_slice_zeroInflatedPoisson.R).
The main thing I love about slice.sample (and why it is used in Rankin & Marsh (2020)) is because, unlike JAGS/BUGs, we can interweave slice-sampling with other Monte Carlo steps, in R.
For example, dynamic imputation of missing data, per MCMC iteration.. Or, we may want to subsample the dadta per iteration. Mixing data with stochastic variables is difficult BUGS/JAGS, but trivial using R and slice.sample
See the following script which showcases dynamic data-imputation:
demo/demo_data-imputation.R- script demonstrating dynamic data imputation
In the folloing example, imagine our missing data consists of "min/max/best-guess"-type data. This is common in wildlife biology, where field-biologists often have to guess the min/max of things, like, counts of dolphins.
| counts | min | best-guess | max |
|---|---|---|---|
| 12 | |||
| 30 | |||
| 1 | |||
| NA | 20 | 25 | 35 |
| 3 | |||
| NA | 1 | 2 | 5 |
| ... |
x_star <- x.init # initalize `x` variables to sample
# mcmc
for(j in 1:n_mcmc){
# STEP 1: data imputation : sample min/best/max
y_imputed <- y # copy raw data with missing data
# loop through missing values to imput
for(idx in idx_missing){
# impute y using min/best/max function
y_min <- y[idx, 'min']; y_max <- y[idx,'max']; y_best <- y[idx,'best']
y_imputed[idx,'count'] <- impute(y_min,y_best,y_max)
} # done dynamic imputation
# add (dynamic) imputed data to the `data_likelihood` input for slice.sample
data_likelihood <- list(y = y_imputed[,'count'],mm = X)
# STEP 2: slice-sample from posteriors conditional on y-imputed
slice_samps <- slice.sample(
x_star, # initial estimates of variables
list_log_posteriors, # list of log-posterior densities per variable
data_likelihood, # y data and model-matrices
list_prior_parameters, # hyperparameters for priors
nslice=4, # number of slices
x.lowb, # lower safety bounds on variables
x.uppb, # upper safety bounds on variables
w=w, # W hyperparameter governing Slice Sampler (see Details)
m=12 # number of steps of W (see Details)
)
# update x_star with last sample from slice-sampler
x_star <- tail(slice_samps$samples, 1)[1,]
# moving average update of the `W` parameter (SEE BACKGROUND to learn more)
w_star <- slice_samps$w
w <- 0.8*w + 0.2*w_star # moving average of w
# store MCMC sample
mcmc_samples[j,]<- x_star
}
One advantage of the Flexible-R-SliceSampler is with Hierarchical models and random-effects model -- with these models, the prior-parameters of one variable are themselves belonging to a distribution, which has a "Hyperprior" on top of it.
In this example (demo/demo_random-effectgs.R), we demonstrate how to run a random-intercept and random-slope regression model: the grouping variable is n=40 individuals, each with T=4 observations. Each individual will have there own random-effects intercept and slope (epsilon). The random-effects come from a Normal distribution governmed by sigma, which itself has a hyperprior: a half-Student-T distribution that concentrates a lot of density around 0 (no variance among random-effects), but long-tails.
We show that JAGS mixes poorly and has high variance for such random-effects models, when there isn't a lot of data.
In contrast, the Flexible-R-SliceSampler mixes beautifully, and adapts easily, and more accurately producing lower-variance estimates.
The only challenge with random-effects models in Flexible-R-SliceSampler is passing the prior-parameters sigma for the random-effects: they are both a variable in x.init to sample, as well as parameter controlling other variables (the epsilons). Our solution is to just make the "prior parameters" of epsilons an index that grabs the sigmas from the x vector of dynamic variables.
Here is our log-posterior function for the random-effects epsilons, which have sigma as their prior-parameters. The model is a Poisson regression with random-intercepts and random-slopes
log_posterior_REregression_dnorm_REprior <- function(x_target,
x_all,
data_likelihood,
prior_parameters
){
# data for likelihood: y values
Y <- data_likelihood$Y
X <- data_likelihood$X
n <- data_likelihood$n
names_fixedeffects <- data_likelihood$names_fixedeffects
names_randomeffects <- data_likelihood$names_randomeffects
names_sigmas <- data_likelihood$names_sigmas
# get fixed effects
betas_vector <- x_all[names_fixedeffects]
# get random effects
epsilons_vector <- x_all[names_randomeffects]
# get names of sigmas (hyperprior)
sigmas <- x_all[names_sigmas]
# matrices for fixed and random effects
BETAS <- matrix(betas_vector, nrow=2, ncol=n)
EPS <- matrix(epsilons_vector, 2, ncol=n,byrow=TRUE)
# expected values of count-distribution (combine fixed and random effects)
LAMBDA <- exp(X%*%BETAS + X%*%EPS)
# loglikelihood
loglike <- sum(dpois(
x=as.numeric(Y), # vectorize observations
lambda=as.numeric(LAMBDA), # vectorize expectations
log=TRUE
))
# normal prior on betas
log_prior <- dnorm(
x=x_target,
mean=0,
sd=sigmas[prior_parameters$which_sigma_idx], # notice how we grab sigma
log=TRUE
)
return(loglike + log_prior)}See the full script in demos/demo_random-effects.R
In contrast, JAGS mixes much worse and has higher-variance estimates that are less accurate. The Flexible-R-SliceSampler does much better than JAGS for random-effects models... But it can be tricky to code it up properly.
If you use this slice-sampler, please cite the following study:
Rankin RW, Marsh H. 2020. Technical Appendices: 8-11 in Marsh H, Collins K. Grech A., Miller R and Rankin RW. 2020. *An assessment of the distribution and abundance of dugongs and in-water, large marine turtles along the Queensland coast from Cape York to Hinchinbrook Island.* A report to the Great Barrier Reef Marine Park Authority, April 2020.
The original Slice Samplier paper by Neal 2003 should be cited as:
Neal, R. M. 2003. Slice sampling. The Annals of Statistics 31:705–767.